Verteilungen berechnen

Wenn $A$ die gegebene Übergangsmatrix zu einem Prozess ist und dir eine zugehörige Startverteilung durch den Verteilungsvektor $\overrightarrow{v_0}$ gegeben ist, kannst du die Verteilung nach $t$ Zeitschritten mit folgender Formel berechnen:

$\overrightarrow{v_t} = A \cdot \overrightarrow{v_{t-1}} = A^t\cdot \overrightarrow{v_0}$

Entsprechend der Reihenfolge der verschiedenen Zustände in der Übergangsmatrix, gibt der erste Eintrag des Verteilungsvektors z.B. die Anzahl der Individuen im ersten Stadium, der zweite Eintrag die der Individuen im zweiten Stadium usw. an.

Beispiel

Zum 01.01.2002 wurde in der EU die Euro-Münze in Umlauf gebracht. Für die dann entstandenen „Münzwanderung pro Jahr“ zwischen den Gebieten Deutschland (D), Frankreich (F) und sonstigen Länder (S) sollte sich die jährlichen Wanderungsanteile gemäß der folgenden Übergangsmatrix verhalten:

		von:	$D$	$F$	$S$
	$D$		$\begin{pmatrix}0,88&0,06&0,15\\[2pt]0,06&0,9&0,05\\[2pt]0,06&0,04&0,8\end{pmatrix}$
nach:	$F$	$M=$
	$S$

Ermittle die prozentuale Verteilung der „deutschen“ Münzen auf die drei Gebiete (D, F, S) zum 01.01.2003 und 01.01.2004. Gehe davon aus, das sich am 01.01.2002 $100\%$ der Münzen in Deutschland befinden.

$\begin{pmatrix} 0,88 & 0,06 & 0,15\\0,06 & 0,9 & 0,05 \\ 0,06 & 0,04 & 0,8 \end{pmatrix}$ $\cdot$ $\begin{pmatrix} 100\\0\\0 \end{pmatrix}$ $=$ $\begin{pmatrix}88\\6\\6 \end{pmatrix}$

Nach einem Jahr befinden sich $88\%$ der deutschen Münzen in D, $6\%$ in F und $6\%$ in S.

$\begin{pmatrix} 0,88 & 0,06 & 0,15\\0,06 & 0,9 & 0,05 \\ 0,06 & 0,04 & 0,8 \end{pmatrix}$ $\cdot$ $\begin{pmatrix} 88\\6\\6 \end{pmatrix}$ $=$ $\begin{pmatrix}78,7\\10,98\\10,32 \end{pmatrix}$

Nach zwei Jahren befinden sich $78,7\%$ der deutschen Münzen in D, $10,98\%$ in F und $10,32\%$ in S.

Ein Restaurant bietet Plätze in drei Bereichen an: der Gaststätte $G$ , im Biergarten $B$ und auf der Dachterrasse $D$ . Am Ende des Jahres untersucht der Besitzer der Gaststätte, welcher der drei Bereiche am liebsten genutzt wird. Dazu untersucht er das Sitzverhalten seiner 800 Stammgäste.

Im Jahr 2012 hat der Gastwirt folgendes Verhalten der Stammkunden des Restaurants festgestellt:

$\small{50\,\%}$ der Stammkunden wählen bei ihrem nächsten Besuch wieder den gleichen Bereich.

Von den Stammkunden, die in der Gaststätte aßen, wechseln bei ihrem nächsten Besuch $\small{30\,\%}$ auf die Dachterrasse und $\small{20\,\%}$ in den Biergarten.

Von den Stammkunden, die im Biergarten aßen, wechseln bei ihrem nächsten Besuch $\small{50\,\%}$ auf die Dachterrasse.

Von den Stammkunden, die auf der Dachterrasse aßen, wechseln bei ihrem nächsten Besuch $\small{25\,\%}$ in die Gaststätte und $\small{25\,\%}$ in den Biergarten.

Stelle eine Übergangsmatrix auf, die das Verhalten der Stammgäste beschreibt.

Aufgrund von Wetterveränderungen wird im folgenden Jahr eine veränderte Übergangsmatrix $A$ bestimmt. Die Anzahl das Stammkunden hat sich jedoch nicht geändert.

		von:	$G$	$B$	$D$
	$G$		$\begin{pmatrix}0,4&0,2&0\\[2pt]0,3&0,5&0,4\\[2pt]0,3&0,3&0,6\end{pmatrix}$
nach:	$B$	$A=$
	$D$

(1)

Gib drei Änderungen des Verhaltens gegenüber dem Vorjahr an.

Im Jahr 2012 haben $400$ Stammgäste in der Gaststätte gegessen, $300$ in dem Biergarten und $100$ auf der Dachterrasse.

(2)

Bestimme unter den Bedingungen der Matrix $A$ die zu erwartende Verteilung für das Jahr 2013.

(3)

Bestimme außerdem die Verteilung für das übernächste Jahr.

Wegen Umbaumaßnahmen im Jahr 2013 auf der Dachterrasse essen nur noch $\small{5\,\%}$ (gemessen an der Anzahl der Gäste im Jahr 2012) der Gäste erneut auf der Dachterrasse. Das Verhalten der Gäste die in der Gaststätte oder dem Biergarten essen und die Anzahl der Stammgäste ändert sich nicht.

(1)

Erkläre, dass das Verhalten durch folgende Matrix $M$ beschrieben werden kann:

		von:	$G$	$B$	$D$
	$G$		$\begin{pmatrix}0,4&0,2&q\\[2pt]0,3&0,5&0,95-q\\[2pt]0,3&0,3&0,05\end{pmatrix}$
nach:	$B$	$M=$
	$D$

(2)

Berechne den Wert $q$ für den Fall, dass im Jahr 2013 genau 250 Gäste in der Gaststätte gegessen haben. Gehe von den in Teilaufgabe b) angegebenen Bedingungen aus.

In einem Labor wird die Entwicklung von Schmetterlingen beobachtet. Dazu gehören die drei Entwicklungsstadien als Raupe $R$ , die Umwandlung im Kokon $K$ und als Schmetterling $S$ . Zu Beginn eines festen Zeitraums, auf den sich im Folgenden die Übergänge zwischen den Entwicklungsstadien beziehen, wird eine Bestandsaufnahme durchgeführt. Dabei wird bei der Übergangsquote berücksichtigt, dass manche Raupen oder Schmetterlinge nicht überleben.

Am Ende des ersten Beobachtungszeitraums befinden sich $\small{25\,\%}$ der Tiere in dem Raupenstadium. $\small{70\,\%}$ der Raupen bilden einen Kokon. Von den Kokons bleiben $\small{55\,\%}$ bestehen, während aus $\small{40\,\%}$ Schmetterlinge schlüpfen. $\small{95\,\%}$ der Schmetterlinge überleben.

Stelle eine Übergangsmatrix $A$ auf.

Zu Beginn der Beobachtung gibt es 152 Raupen, 52 Kokons und 116 Schmetterlinge.

(1)

Bestimme die jeweilige Anzahl der Tieren in den Entwicklungsstadien am Ende des ersten Beobachtungszeitraums.

(2)

Berechne nach welchem Beobachtungszeitraum erstmals weniger als $\small{75\,\%}$ des ursprünglichen Gesamtbestands der Tiere vorhanden sind.

Das Forschungslabor untersucht, ob der Einsatz eines bestimmten Pestizids für die Raupen bzw. Schmetterlinge schädlich ist. Es wird folgende Übergangsmatrix bestimmt:

		von:	$R$	$K$	$S$
	$R$		$\begin{pmatrix}0,25&0&0\\[2pt]0,7&0,55&0\\[2pt]0&0,4&0,7\end{pmatrix}$
nach:	$K$	$B=$
	$S$

(1)

Beurteile anhand der Matrix, ob das Pestizid für die Raupen bzw. Schmetterlinge schädlich ist.

(2)

Um wieviel Prozent ging der Bestand der Schmetterlinge bei dem Einsatz des Pestizids nach dem ersten Beobachtungszeitraum zurück?

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Die Übergangsmatrix bestimmen

Um die Übergangsmatrix zu bestimmen, kannst du den Übergangsgraph zu Hilfe nehmen.
Tipp: Wenn du das Aufgabenblatt zum Thema Übergangsgraphen bearbeitet hast, hast du die Übergangsgraphen in Aufgabe 2a) schon gebildet.

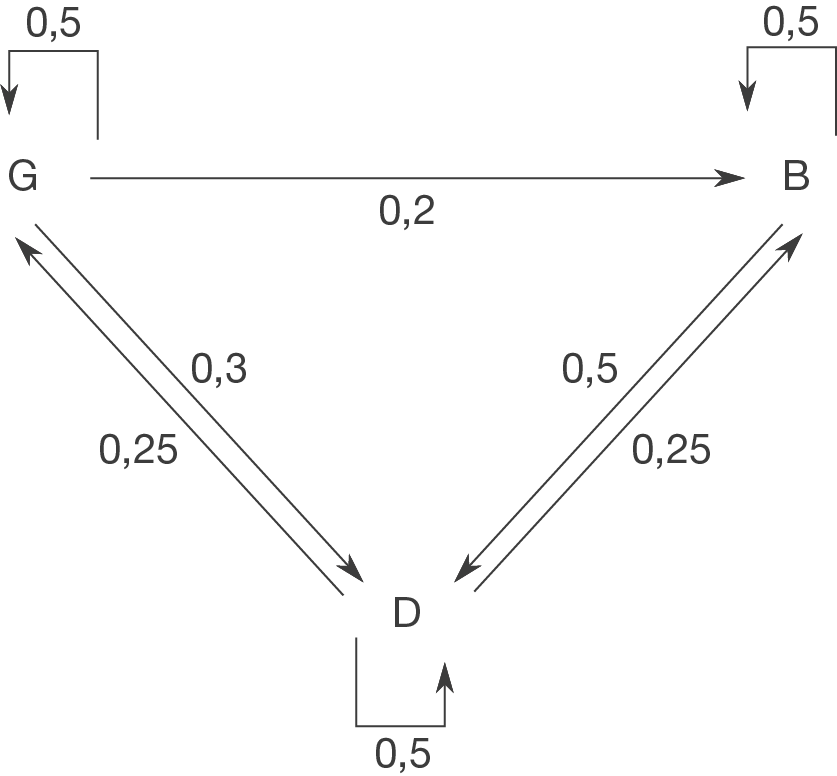Diagramm mit Knoten G, B und D sowie Pfeilen, die Wahrscheinlichkeiten darstellen.

Die Übergangsmatrix lautet demnach:

		von:	$G$	$B$	$D$
	$G$		$\begin{pmatrix}0,5&0&0,25\\[2pt]0,2&0,5&0,25\\[2pt]0,3&0,5&0,5\end{pmatrix}$
nach:	$B$	$M=$
	$D$

(1) Veränderung des Verhaltens

Der Eintrag in der ersten Spalte, erste Zeile gibt an, dass $\small{10\,\%}$ weniger der Gäste erneut in der Gaststätte essen als im Vorjahr. Stattdessen wecheln jedoch $\small{20\,\%}$ mehr Gäste von dem Biergarten in die Gaststätte (zweite Spalte, erste Zeile). Eine dritte Veränderung ist, dass $\small{10\,\%}$ mehr von der Gaststätte in den Biergarten wechseln (erste Spalte, zweite Zeile). Es gibt noch mehr Veränderungen in der Matrix. Die genannten sind nur Beispiele.

(2) Verteilung im Jahr 2013 berechnen

Um die Verteilung für das Jahr 2013 zu bekommen, multiplizierst du die Matrix $A$ mit der Anzahl der Gäste in den jeweiligen Sitzbereichen. Die Anfangsverteilung hast du in der Aufgabenstellung gegeben:

$\vec v_0=\begin{pmatrix}400\\300\\100\end{pmatrix}$

Multiplikation der Matrix $A$ mit dem Vektor $\vec v_0$

$\begin{array}{rll} A\cdot\vec v_0&=&\begin{pmatrix}220\\310\\270\end{pmatrix}\\ \end{array}$

Vollständige Lösung anzeigen

Im Jahr 2013 essen 220 Stammgäste in der Gaststätte, 310 in dem Biergarten und 270 auf der Dachterrasse.

(3) Verteilung im übernächsten Jahr (2014) berechnen

Hier hast du nun zwei Möglichkeiten die Verteilung im Jahr 2014 zu berechnen. Entweder du multiplizierst den Vektor $\vec v_1$ , der die Verteilung im Jahr 2013 beschreibt, mit der Matrix (Lösungsweg A), oder du quadrierst die Matrix und multiplizierst sie mit der Anfangsverteilung $\vec v_0$ (Lösungsweg B).

$\blacktriangleright$ Lösungsweg A: Multiplikation Matrix $A$ mit Vektor $\vec v_1$

$\begin{array}{rll} A\cdot\vec v_1&=&\begin{pmatrix}150\\329\\321\end{pmatrix} \end{array}$

Vollständige Lösung anzeigen

In dem Jahr essen 150 Stammgäste in der Gaststätte, 329 in dem Biergarten und 321 auf der Dachterrasse.

$\blacktriangleright$ Lösungsweg B: Quadrierung Matrix $A$ und Multiplikation mit Vektor $\vec v_0$

1. Schritt: Quadrierung der Matrix $A$ :

Um die Matrix $A$ zu quadrieren, bildest du das Matrizenprodukt. Dazu multiplizierst du die jeweilige Zeile der einen Matrix mit den Spalten der zweiten Matrix. Zunächst werden also die Zeilen jeweils mit der ersten Spalte multipliziert. Dadurch erhältst du die erste Spalte der neuen Matrix. Dann werden die Zeilen jeweils mit der zweiten bzw. dritten Spalte multipliziert.

$\begin{array}{rll} A^2&=&... \end{array}$

Vollständige Lösung anzeigen

2. Schritt: Multiplikation von $A^2$ mit dem Vektor $\vec v_0$

$\begin{array}{rll} A^2\cdot\vec v_0&=&\begin{pmatrix}150\\329\\321\end{pmatrix} \end{array}$

Vollständige Lösung anzeigen

In dem Jahr essen 150 Stammgäste in der Gaststätte, 329 in dem Biergarten und 321 auf der Dachterrasse.

(1) Erklärung der Matrix

Die Anzahl der Stammgäste bleibt konstant. Das heißt, dass sie sich jeweils zu $\small{100\,\%}$ auf die drei Bereiche der Gaststätte verteilen. Wenn jetzt nur $\small{5\,\%}$ der Stammgäste erneut auf der Dachterrasse essen, hat der Übergang von $D$ zu $D$ den Faktor $\small{0,05}$ . Die restlichen $\small{95\,\%}$ der Gäste wechseln von der Dachterrasse in die Gaststätte oder in den Biergarten. Es wechselt demnach ein unbestimmter Anteil $q$ von der Dachterrasse in die Gaststätte. Also wechselt ein Anteil von $\small{0,95}-q$ von der Dachterrasse in den Biergarten. Der Wert $q$ kann also Werte zwischen $\small{0}$ und $\small{0,95}$ annehmen, da der Eintrag nicht negativ werden kann und nicht mehr als $\small{95\,\%}$ betragen darf.

(2) Berechnung von $q$

Die ersten Zeile der Matrix gibt die Übergangsquoten der Stammgäste an, die in die Gaststätte wechseln. $\small{40\,\%}$ der Gäste gehen wie im Jahr 2012 erneut in die Gaststätte. $\small{20\,\%}$ wechseln von dem Biergarten in die Gaststätte. Ein unbekannter Anteil $q$ wechselt von der Dachterrasse in die Gaststätte. Die Summe der Stammgäste die in der Gaststätte im Jahr 2013 beträgt insgesamt 250.

Wenn du die absolute Zahl der Übergänge der einzelnen Bereiche bestimmst, kannst du sie mit der Summe gleichsetzen und nach $q$ auflösen. Um die absolute Zahl der Übergänge zu bestimmen, bildest du das Produkt der Anzahl der Gäste in den verschiedenen Bereichen mit den zugehörigen Faktoren.

Die Anzahl der Gäste in den einzelen Bereichen entspricht der im Jahr 2012. In diesem Jahr haben 400 Leute in der Gaststätte gegessen, 300 in dem Biergarten und 100 auf der Dachterrasse.

$\begin{array}{rll} q&=&0,3 \end{array}$

Vollständige Lösung anzeigen

Falls im Jahr 2013 die Anzahl der Gäste, die in der Gaststätte gegessen haben, 250 beträgt, gilt $q=\small{0,3}$ .

Die Übergangsmatrix bestimmen

Das Raupenstadium wird mit $R$ abgekürzt. Für den Kokon wird ein $K$ geschrieben und für das Schmetterlingstadium ein $S$ . Um die Übergangsmatrix zu bestimmen, kannst du den Übergangsgraph zur Hilfe nehmen. Du kannst sie jedoch auch direkt mit Hilfe der Angaben in der Aufgabenstellung bilden.

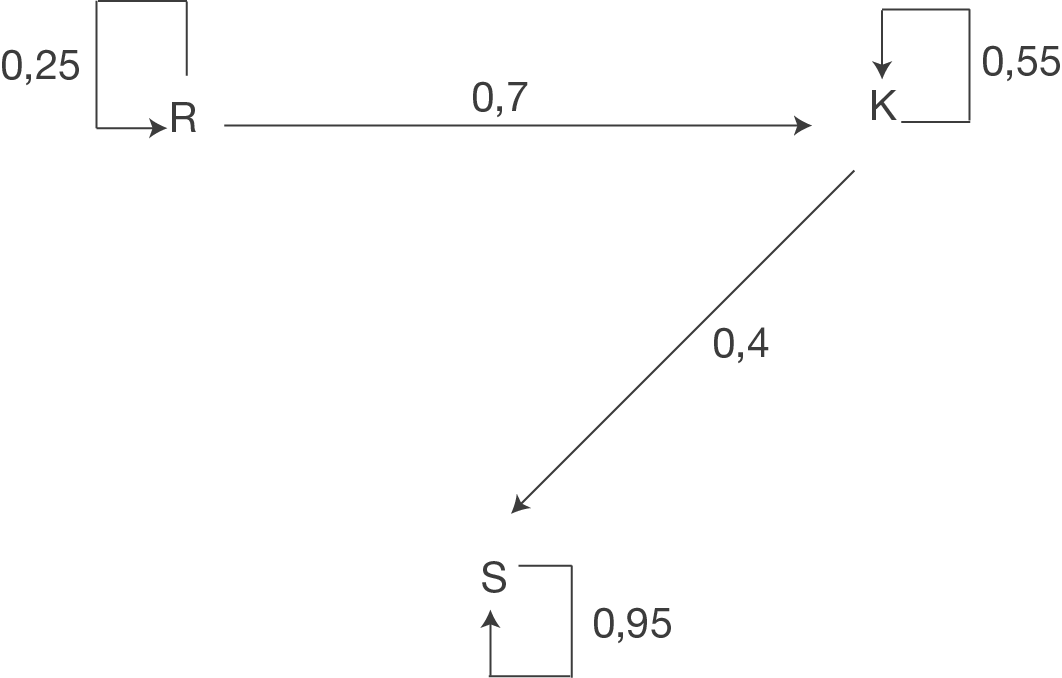Diagramm mit vier Kästchen und Wahrscheinlichkeiten zur Darstellung von Übergängen zwischen Zuständen R, K und S.

Die Übergangsmatrix lautet demnach:

		von:	$R$	$K$	$S$
	$R$		$\begin{pmatrix}0,25&0&0\\[2pt]0,7&0,55&0\\[2pt]0&0,4&0,95\end{pmatrix}$
nach:	$K$	$A=$
	$S$

(1) Verteilung am Ende des 1. Beobachtungszeitraums berechnen

Um die neue Verteilung zu bekommen, multiplizierst du die Matrix $A$ mit der Anzahl der Tiere in den jeweiligen Stadien. Die Anfangsverteilung hast du in der Aufgabenstellung gegeben:

$\vec{v_0}=\begin{pmatrix}152\\52\\116\end{pmatrix}$

Multiplikation der Matrix $A$ mit Vektor $\vec v_0$ :

$\begin{array}{rll} A\cdot\vec v_0&=&\begin{pmatrix}38\\135\\131\end{pmatrix} \end{array}$

Vollständige Lösung anzeigen

Nach dem ersten Beobachtungszeitraum gibt es $\small{38}$ Raupen, $\small{135}$ Kokons und $\small{131}$ Schmetterlinge.

(2) Beobachungszeitraum mit \lt $\small{75\,\%}$ des Anfangsbestands

Hier sollst du berechnen nach wie vielen Beobachtungszeiträumen $n$ nur noch $\small{75\,\%}$ der Tiere des Anfangsbestands leben. Der Anfangsbestand wird mit $B_0$ abgekürzt.

Du weißt, dass nach jedem Beobachtungszeitraum noch $\small{95\,\%}$ der Tiere leben. Nach dem ersten Zeitraum leben also noch $\small{95\,\%}$ von $B_0$ :

$B_1=0,95\cdot B_0$

Nach dem zweiten Beobachtungszeitraum gilt dementsprechend:

$\begin{array}{rll} B_2=0,95\cdot B_1&\\[5pt] B_2=0,95^2\cdot B_0 \end{array}$

Um den Bestand nach $n$ Beobachtungszeiträumen zu bestimmen, kannst du also folgende Gleichung verwenden:

$B_n=0,95^n\cdot B_0$

Der Bestand soll weniger als $\small{75\,\%}$ betragen. Du erhältst diese Ungleichung:

$\begin{array}{rll} 0,95^n\cdot B_0&<&0,75\cdot B_0\\[5pt] n&>&5,61 \end{array}$

Vollständige Lösung anzeigen

Nach 6 Beobachtungszeiträumen gibt es erstmals weniger als $\small{75\,\%}$ des ursprünglichen Bestands der Tiere.

(1) Beurteilung der Schädlichkeit

Hier musst du die Einträge der Matrizen $A$ und $B$ vergleichen. Du siehst, dass sich nur der Eintrag von dem Übergang von $S$ zu $S$ sich geändert hat. Statt $\small{95\,\%}$ der Schmetterlinge überleben nur noch $\small{70\,\%}$ . Das bedeutet, dass das Pestizid schädlich für Schmetterlinge ist. Dies gilt jedoch nicht für die Raupen. Die Anzahl der Raupen verändert sich nicht. Das Pestizid ist also für Raupen ungefährlich.

(2) Rückgang des Bestands in Prozent

Du weißt, dass zu Beginn des Beobachtungszeitraums 116 Schmetterlinge leben. Um zu berechnen, wie viele nach dem Zeitraum noch leben, bildest du das Produkt der Matrix $B$ mit dem Vektor $\vec v_0$ . Mit dem Anfangsbestand und dem Bestand nach dem ersten Beobachtungszeitraums kannst du den Rückgang in Prozent berechnen. Dazu benötigst du die Prozentformel:

$p=\dfrac{W}{G}\cdot100$

Dabei ist $p$ der Prozentsatz, $W$ der Prozentwert und $G$ der Grundwert.

1. Schritt: Berechnung des Bestands nach 1. Beobachtungszeitraum

$\begin{array}{rll} B\cdot \vec v_0&=&\begin{pmatrix}38\\135\\102\end{pmatrix} \end{array}$

Vollständige Lösung anzeigen

Nach dem Einsatz des Pestizids leben nach dem ersten Beobachtungszeitraums noch 102 Schmetterlinge.

2. Schritt: Berechnung des Rückgangs in Prozent

Nun kannst du die Werte in die Prozentformel einsetzen. Dabei suchst du den Prozentsatz. Der Grundwert entspricht dem Anfangsbestand, der Prozentwert dem Bestand nach dem ersten Beobachtungszeitraum.

$\begin{array}{rll} p&=&\dfrac{W}{G}\cdot100\\[5pt] p&=&\dfrac{102}{116}\cdot100\\[5pt] p&=&87,9\,\% \end{array}$

Vor dem Einsatz entspricht der Bestand $\small{100\,\%}$ . Nun beträgt er nur noch $\small{87,9\,\%}$ . Der Bestand der Schmetterlinge ging nach dem Einsatz des Pestizids im ersten Beobachtungszeitraum demnach um $\small{12,1\,\%}$ zurück.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?