Vermischte Aufgaben

Die Gerade $h$ ist parallel zur $z$ -Achse und geht durch den Punkt $A(4\mid10\mid0)$ . Es gibt eine Gerade durch den Punkt $B(8\mid4\mid2)$ , welche die Gerade

$g:\;\overrightarrow{x}=\left(\begin{array}{r} 12\\ 0\\ 0\\ \end{array}\right)+t\left(\begin{array}{r} -12\\ 6\\ 0\\ \end{array}\right)$ $;\;t\in\mathbb{R}$

und $h$ schneidet. Ermittle eine Gleichung dieser Geraden.

Untersuche, ob eine Seite des Dreiecks $ABC$ mit $A(2\mid1\mid5)$ , $B(3\mid4\mid1)$ und $C(0\mid0\mid1)$ auf der Geraden

$g:\;\overrightarrow{x}=\left( {\begin{array}{*{20}r} -9 \\ -32 \\ 49 \\ \end{array}} \right)+t\left( {\begin{array}{*{20}r} -4 \\ -12 \\ 16 \\ \end{array}} \right)$

liegt.

Wie lang ist diese Seite?

Begründe, dass die Gerade

$g:\;\overrightarrow{x}=s\cdot \left( {\begin{array}{*{20}r} 4 \\ { - 10} \\ 2 \\ \end{array}} \right)\quad s\in\mathbb{R}$

parallel zur Verbindungsgeraden $h$ der Punkte $P(2\mid-1\mid3)$ und $Q(0\mid4\mid2)$ ist.

Gib eine Gleichung für die Mittelparallele von $g$ und $h$ an.

Im Folgenden soll eine ägyptische Pyramide durch die Eckpunkte der Grundfläche $A(3\mid8\mid0)$ , $B(12\mid11\mid0)$ , $C(9\mid20\mid0)$ und $D(0\mid17\mid0)$ dargestellt werden. Die Spitze der Pyramide befindet sich an der Stelle $S(6\mid14\mid10)$ .

Weise nach, dass es sich um eine quadratische regelmäßige Pyramide handelt.

Paralleles Sonnenlicht fällt in Richtung $\overrightarrow{v}=\left(\begin{array}{r} 0\\ -4\\ -3\\ \end{array}\right)$ ein.

Bestimme den Schattenpunkt $\(S$ der Pyramidenspitze $S$ in der $x,y$ -Ebene.

Von einem senkrechten Kegel kennt man die Koordinaten der Spitze $S$ , die Koordinaten eines Punktes $P$ des Grundkreises sowie eine Koordinatengleichung der Ebene $E$ , in der der Grundkreis liegt.

Beschreibe ein Verfahren, um den Mittelpunkt $M$ und den Radius $r$ des Grundkreises zu bestimmen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Die Gerade $h$ ist parallel zur $z$ -Achse und geht durch den Punkt $A(4\mid10\mid0)$ .

Aufstellen einer Gleichung von $h$

$h:\;\overrightarrow{x}$ = $\left(\begin{array}{r} 4\\ 10\\ 0\\ \end{array}\right)+u\cdot\left(\begin{array}{r} 0\\ 0\\ 1\\ \end{array}\right)$ $;\;u\in\mathbb{R}$

Der Punkt $B(8\mid4\mid2)$ liegt nicht auf der Geraden $h$ , da

$\begin{array}[t]{rll} 8\neq&4+0\cdot u&\\ \end{array}$

Vollständige Lösung anzeigen

Skizze:

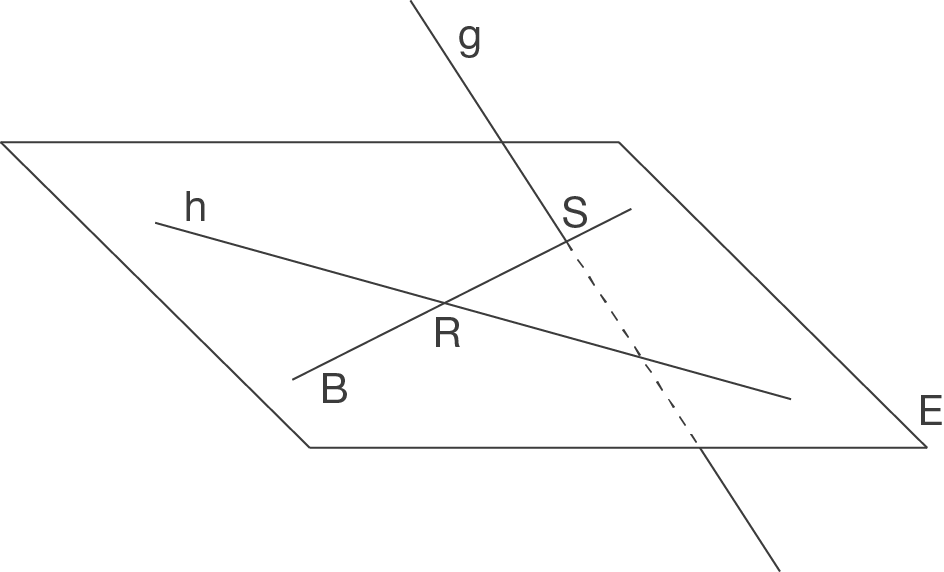Diagramm mit Linien und Ebenen, beschriftet mit Buchstaben und einer gestrichelten Linie.

Die gesuchte Gerade muss daher in der von $B$ und $h$ bestimmten Ebene $E$ liegen.

Mit $\overrightarrow{AB}$ = $\left(\begin{array}{r} 4\\ -6\\ 2\\ \end{array}\right)$ und dem Richtungsvektor von $h$ erhält man eine Parameterform der Ebene $E$ .

$E$ :

Vollständige Lösung anzeigen

Bestimmung einer Koordinatenform von $E$

Ein Normalenvektor von $E$ bestimmt man über

$\left(\begin{array}{r} 0\\ 0\\ 1\\ \end{array}\right)\circ\left(\begin{array}{r} n_1\\ n_2\\ n_3\\ \end{array}\right)$ = $1n_3=0$ $\quad n_3=0$ und

$\left(\begin{array}{r} 4\\ -6\\ 2\\ \end{array}\right)\circ\left(\begin{array}{r} n_1\\ n_2\\ n_3\\ \end{array}\right)$ = $4n_1-6n_2+2n_3\\=0$

Für $n_3=0$ ergibt sich $4n_1-6n_2=0$ . Ein möglicher Normalenvektor von $E$ ist somit $\overrightarrow{n}=\left(\begin{array}{r} 3\\ 2\\ 0\\ \end{array}\right)$ .

Damit erhält man folgende Koordinatenform: $\;E:\;3x+2y=d$

Den Parameter $d$ kann man nun mit dem Punkt $A(4\mid10\mid0)$ , der auf der Ebene $E$ liegt, bestimmen. Setze $A$ in die Koordinatenform ein:

$3\cdot 4 +2\cdot 10=32=d$ $\quad E:\;3x+2y=32$

Schnitt von $E$ mit der Gerade $g:\;\overrightarrow{x}=\left(\begin{array}{r} 12\\ 0\\ 0\\ \end{array}\right)+t\left(\begin{array}{r} -12\\ 6\\ 0\\ \end{array}\right)$ $;\;t\in\mathbb{R}$

Einsetzen der Gerade $g$ in Koordinaten- form der Ebene $E$ :

$3(12-12t)+2\cdot6t=32$ $\quad t=\dfrac{1}{6}$

Einsetzen von $t$ in $g$ liefert den Schnitt- punkt $S$

$\overrightarrow{OS}$ = $\left(\begin{array}{r} 12\\ 0\\ 0\\ \end{array}\right)+\dfrac{1}{6}\cdot\left(\begin{array}{r} -12\\ 6\\ 0\\ \end{array}\right)$ = $\left(\begin{array}{r} 10\\ 1\\ 0\\ \end{array}\right)$ $\quad S(10;1;0)$

Die Verbindungsgerade $BS$ : $\overrightarrow{x}$ = $\left(\begin{array}{r} 8\\ 4\\ 2\\ \end{array}\right)+m\cdot\left(\begin{array}{r} 2\\ -3\\ -2\\ \end{array}\right);$ $\;m\in\mathbb{R}$ ist nicht parallel zur Geraden $h$ , da die Richtungsvektoren linear unabhängig sind.

Da beide Geraden in der Ebenen $E$ lie- gen, schneidet $BS$ auch $h$ in einem Punkt $R$ .

Die Gerade $BS$ : $\overrightarrow{x}$ = $\left(\begin{array}{r} 8\\ 4\\ 2\\ \end{array}\right)+m\cdot\left(\begin{array}{r} 2\\ -3\\ -2\\ \end{array}\right)$ $;\;m\in\mathbb{R}$ schneidet somit die beiden Geraden $h$ und $g$ .

Damit eine Seite des Dreiecks auf der Geraden $g:\;\overrightarrow{x}$ = $\left( {\begin{array}{*{20}r} -9 \\ -32 \\ 49 \\ \end{array}} \right)+t\left( {\begin{array}{*{20}r} -4 \\ -12 \\ 16 \\ \end{array}} \right)$ liegt, müssen zwei der drei Punkte auf $g$ liegen. Führe also je eine Punktprobe durch, indem du gleichsetzt.

$\begin{pmatrix}11\\33\\-44 \end{pmatrix}=\begin{pmatrix} -4t \\-12 t \\16t \end{pmatrix}$

Vollständige Lösung anzeigen

Daraus erhältst du folgendes lineares Gleichungssystem:

$\begin{array}{} \text{I}\quad&11&=&-4t\quad\\ \text{II}\quad&33&=&-12t\quad\\ \text{III}\quad&-44&=&16t\quad\\ \end{array}$

Löse nun $\text{I}$ nach $t$ auf:

$\begin{array}[t]{rll} 11&=&-4t &\quad \scriptsize \mid\; :(-4)\\[5pt] -\frac{11}{4}&=& t \end{array}$

Setze diese Lösung nun in die anderen beiden Gleichungen ein. Werden diese ebenfalls erfüllt, liegt $A$ auf der Geraden $g$ , andernfalls nicht.

$\begin{array}[t]{rll} 33&=& -12t &\quad \scriptsize \\[5pt] 33&=& -12\cdot \left(-\frac{11}{4}\right)&\quad \scriptsize \\[5pt] 33&=& 33 \end{array}$

Einsetzen in $\text{III}$ liefert:

$\begin{array}[t]{rll} -44&=& 16t&\quad \scriptsize \\[5pt] -44&=&16\cdot \left(-\frac{11}{4}\right)&\quad \scriptsize \\[5pt] -44&=& -44 &\quad \scriptsize \\[5pt] \end{array}$

Beide Gleichungen werden ebenfalls erfüllt, also liegt der Punkt $A$ auf der Geraden $g$ . Für die übrigen beiden Punkte kannst du analog vorgehen. Für $B$ ergibt sich folgende Gleichung:

$\begin{pmatrix}12\\36\\-48 \end{pmatrix}=\begin{pmatrix} -4t \\-12 t \\16t \end{pmatrix}$

Vollständige Lösung anzeigen

$\begin{array}{} \text{I}\quad&12&=&-4t\quad\\ \text{II}\quad&36&=&-12t\quad\\ \text{III}\quad&-48&=&16t\quad\\ \end{array}$

Löse nun $\text{I}$ nach $t$ auf:

$\begin{array}[t]{rll} 12&=&-4t &\quad \scriptsize \mid\; :(-4)\\[5pt] -3&=& t \end{array}$

Setze diese Lösung nun in die anderen beiden Gleichungen ein. Werden diese ebenfalls erfüllt, liegt $B$ auf der Geraden $g$ , andernfalls nicht.

$\begin{array}[t]{rll} 36&=& -12t &\quad \scriptsize \\[5pt] 36&=& -12\cdot \left(-3\right)&\quad \scriptsize \\[5pt] 36&=& 36 \end{array}$

Einsetzen in $\text{III}$ liefert:

$\begin{array}[t]{rll} -48&=& 16t&\quad \scriptsize \\[5pt] -48&=& 16\cdot (-3)&\quad \scriptsize \\[5pt] -48&=& -48 &\quad \scriptsize \\[5pt] \end{array}$

Beide Gleichungen werden ebenfalls erfüllt, also liegt der Punkt $B$ auf der Geraden $g$ . Für $C$ ergibt sich folgende Gleichung:

$\begin{pmatrix}9\\32\\-48 \end{pmatrix}=\begin{pmatrix} -4t \\-12 t \\16t \end{pmatrix}$

Vollständige Lösung anzeigen

Löse nun $\text{I}$ nach $t$ auf:

$\begin{array}[t]{rll} 9&=&-4t &\quad \scriptsize \mid\; :(-4)\\[5pt] \frac{-9}{4}&=& t \end{array}$

Setze diese Lösung nun in die anderen beiden Gleichungen ein. Werden diese ebenfalls erfüllt, liegt $C$ auf der Geraden $g$ , andernfalls nicht.

$\begin{array}[t]{rll} 32&=& -12t &\quad \scriptsize \\[5pt] 32&=& -12\cdot \left(\frac{-9}{4}\right)&\quad \scriptsize \\[5pt] 32&=& 27 & \text{Widerspruch} \end{array}$

Diese Gleichung wird nicht erfüllt. Der Punkt $C$ liegt also nicht auf $g$ . Insgesamt erhältst du, dass die Seite $\overline{AB}$ auf der Geraden $g$ liegt.

Die Länge der Seite berechnet sich über den Abstand zwischen $A$ und $B$ :

$\left| \overline{AB}\right| = \sqrt{26} \approx 5,1$

Vollständige Lösung anzeigen

Die Seite $\overline{AB}$ ist ungefähr $5,1$ cm lang.

Eine Gleichung der Verbindungsgeraden $h$ der Punkte $P(2\mid-1\mid3)$ und $Q(0\mid4\mid2)$ ist:

$h:\;\overrightarrow{x}$ = $\overrightarrow{OP}+t\cdot\overrightarrow{PQ}$ $=\left( {\begin{array}{*{20}r} 2 \\ { - 1} \\ 3 \\ \end{array}} \right)+t\cdot \left( {\begin{array}{*{20}r} -2 \\ { 5} \\ -1 \\ \end{array}} \right);\quad t\in\mathbb{R}$

Die Gerade

$g:\;\overrightarrow{x}$ = $s\cdot \left( {\begin{array}{*{20}r} 4 \\ { - 10} \\ 2 \\ \end{array}} \right)\quad s\in\mathbb{R}$

ist parallel zu $h$ , da die Richtungsvek- toren wegen

$\left( {\begin{array}{*{20}r} 4 \\ { - 10} \\ 2 \\ \end{array}} \right)=(-2)\cdot\left( {\begin{array}{*{20}r} -2 \\ { 5} \\ -1 \\ \end{array}} \right)$

linear abhängig sind.

Berechnung der Mittelparallelen:

Der Punkt $P(2\mid-1\mid3)$ liegt auf $h$ , der Punkt $(0\mid0\mid0)$ auf $g$ . Die Mittelparallele $k$ von $g$ und $h$ muss daher durch den Mittelpunkt $M\left(1\middle|-\frac{1}{2}\middle|\frac{3}{2}\right)$ der Strecke $OP$ gehen. $M$ kann daher als Stützvektor von $k$ gewählt werden. Die Richtungsvektoren von $k$ , $g$ und $h$ sind linear abhängig. Die Mittelparallele von $g$ und $h$ ist daher gegeben durch:

$k:$

Vollständige Lösung anzeigen

Gegeben sind die Punkte $A(3\mid8\mid0)$ , $B(12\mid11\mid0)$ , $C(9\mid20\mid0)$ , $D(0\mid17\mid0)$ und $S(6\mid14\mid10)$ .

Für die Vektoren, die die Seiten der Grundfläche beschreiben, gilt

$\overrightarrow{AB}$ $=\overrightarrow{DC}$ $=\left(\begin{array}{r} 9\\ 3\\ 0\\ \end{array}\right)$ ; $\;\;$ $\overrightarrow{AD}$ $=\overrightarrow{BC}$ $=\left(\begin{array}{r} -3\\ 9\\ 0\\ \end{array}\right)$

Es gilt $\;\left|\overrightarrow{AB}\right|$ $=\left|\overrightarrow{DC}\right|$ $=\left|\overrightarrow{AD}\right|$ $=\left|\overrightarrow{BC}\right|$ $=\sqrt{90}$

Alle Seiten sind also gleich lang. Überprüfe nun noch, ob die Seiten im rechten Winkel zueinander stehen, indem du die Umkehrung des Satzes des Pythagoras verwendest. Wenn der Satz des Pythagoras $a^2+b^2=c^2$ gilt, besitzt das betrachtete Dreieck einen rechten Winkel zwischen den Seiten $a$ und $b$ . Betrachte also das Dreieck $ABD$ , der rechte Winkel sollte in diesem Fall im Punkt $B$ liegen. Die Länge der Katheten kennst du bereits: $\left|\overrightarrow{AB}\right| = \left|\overrightarrow{BC}\right| = \sqrt{90}$ . Berechne nun noch die Länge der Hypotenuse:

$\overrightarrow{AC} = \begin{pmatrix}6\\12\\ 0 \end{pmatrix}$ also $\left|\overrightarrow{AC}\right| = \sqrt{6^2+12^2+0^2} = \sqrt{180}$

Vergleiche nun die beiden Längen:

$\left|\overrightarrow{AB}\right|^2 + \left|\overrightarrow{BC}\right|^2$ $= \sqrt{90}^2+\sqrt{90}^2 = 180$

$\left|\overrightarrow{AC}\right|$ $= \sqrt{180}^2 = 180$

Da alle Seiten gleich lang sind und zwischen zwei Seiten ein rechter Winkel liegt, sind alle Winkel rechtwinklig. Es handelt sich somit um eine quadratische Grundfläche.

Für den Lotpunkt von $S$ in der $x,y$ -Ebene gilt $S_{\text{Lot}}(6\mid14\mid0)$ . Da dieser auf der halben Diagonalen $\overrightarrow{AC}$ der Grundfläche liegt,

$\overrightarrow{OS_{\text{Lot}}}=\overrightarrow{OA}+\frac{1}{2}\overrightarrow{AC}$ $=\left(\begin{array}{r} 3\\ 8\\ 0\\ \end{array}\right)+\frac{1}{2}\left(\begin{array}{r} 6\\ 12\\ 0\\ \end{array}\right)$ = $\left(\begin{array}{r} 6\\ 14\\ 0\\ \end{array}\right)$ .

Es handelt sich somit um eine quadratische, regelmäßige Pyramide.

Die Gerade $g$ : $\overrightarrow{x}$ = $\left(\begin{array}{r} 6\\ 14\\ 10\\ \end{array}\right)+s\left(\begin{array}{r} 0\\ -4\\ -3\\ \end{array}\right)$ beschreibt den Verlauf des Lichtstrahls.

Dieser schneidet die $x,y$ -Ebene, wenn $z=0$ gilt.

$10-3s=0$ $\Rightarrow\;s$ = $\dfrac{10}{3}$ . Setzt man $s$ in die Geradengleichung von $g$ ein, so ergibt sich der gesuchte Punkt $S‘$ mit

$g$ : $\overrightarrow{OS‘}$ = $\left(\begin{array}{r} 6\\ 14\\ 10\\ \end{array}\right)+\dfrac{10}{3}\left(\begin{array}{r} 0\\ -4\\ -3\\ \end{array}\right)$ $=\left(\begin{array}{r} 6\\ \frac{2}{3}\\ 0\\ \end{array}\right)$

$\quad S‘\left(6\mid\frac{2}{3}\mid0\right)$

1.Schritt: Mittelpunkt bestimmen

Die zur Ebene senkrecht durch den Punkt $S$ verlaufende Gerade schneidet die Ebene im Mittelpunkt $M$ des Grundkreises.

Diese Gerade besitzt als Richtungsvektor den Normalenvektor der Ebene.

2.Schritt: Radius bestimmen

Der Radius entspricht dem Abstand des Punktes $M$ zu $P$ . Dieser Abstand wird über den Betrag des Verbindungsvektors berechnet ( $r=\left|\overrightarrow{MP}\right|$ ).

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?