Trigonometrische Funktionen
Wenn du den Graphen einer trigonometrischen Funktion (wir betrachten hier nur den Sinus, Kosinus und Tangens und lassen die Umkehrfunktionen aus) zeichnen willst, beachte folgende Punkte:
- Die Sinusfunktion
ist auf ganz
definiert. Der zugehörige Graph ist punktsymmetrisch zum Ursprung. Die Funktion hat die Periode
, d.h.:
, d.h.
Der Wertebereich ist das Intervall.
- Die Kosinusfunktion
ist auf ganz
definiert. Der zugehörige Graph ist achsensymmetrisch zur
-Achse. Die Funktion hat ebenso die Periode
und den Wertebereich
. Der Kosinus ist nichts anderes als eine Verschiebung des Sinus um
nach links, d.h.
- Die Tangensfunktion ist definiert als
, d.h. die Funktion ist bei den Nullstellen der Kosinusfunktion nicht definiert. Zeichne an diesen Stellen senkrechte Asymptoten ein. Die Nullstellen der Tangensfunktion sind gerade die Nullstellen der Sinusfunktion. Die Periode ist
.
- Der Graph einer trigonometrischen Funktion wird entlang der
-Achse verschoben, indem eine Konstante
zu der Funktion addiert bzw. subtrahiert wird, z.B.
. Der Graph der Funktion wird nach rechts verschoben durch die Subtraktion einer Konstanten
in der Klammer, nach links durch die Addition der Konstanten:
- Ist die Funktion mit einem Faktor
multipliziert, streckst du den Graph entlang der
-Achse, ist der Faktor
, stauchst du den Graph entlang der
-Achse:
- Die Periode der Funktion wird vergrößert, indem eine Konstante
in der Klammer multipliziert wird, verkleinert, wenn
ist:
- Der Graph wird an der
-Achse gespiegelt, wenn die Funktion ein negatives Vorzeichen besitzt:
. Du spiegelst die Funktion an der
-Achse, wenn in der Klammer ein negatives Vorzeichen steht
.
1.
Skizziere die Schaubilder folgender Funktionen und gib die Periode an.






a)
b)
c)
d)
e)
f)
2.
Skizziere das Schaubild der Funktion und beschreibe, wie es aus dem Schaubild der Sinus- bzw. der Kosinus-Funktion hervorgeht.






a)
b)
c)
d)
e)
f)
3.
Verschiebe das Schaubild der angegebenen Funktion wie gefordert und gib die Funktionsgleichung der neuen Funktion an.
 Verschiebung um 1 LE in positive x-Richtung („nach rechts“) und um 2 LE in positive y-Richtung („nach oben“)
Verschiebung um 1 LE in positive x-Richtung („nach rechts“) und um 2 LE in positive y-Richtung („nach oben“)
 Verschiebung um 3 LE in negative x-Richtung („nach links“) und um 1 LE in positive y-Richtung („nach oben“)
Verschiebung um 3 LE in negative x-Richtung („nach links“) und um 1 LE in positive y-Richtung („nach oben“)
 Verschiebung um 1 LE in negative x-Richtung („nach links“) und um 4 LE in negative y-Richtung („nach unten“)
Verschiebung um 1 LE in negative x-Richtung („nach links“) und um 4 LE in negative y-Richtung („nach unten“)
 Verschiebung um 2 LE in positive y-Richtung („nach oben“) und Verdopplung der Amplitudenhöhe
Verschiebung um 2 LE in positive y-Richtung („nach oben“) und Verdopplung der Amplitudenhöhe
 Verschiebung um 2 LE in positive x-Richtung („nach rechts“) und anschließende Verdopplung der Periodenlänge
Verschiebung um 2 LE in positive x-Richtung („nach rechts“) und anschließende Verdopplung der Periodenlänge
 Verschiebung um
Verschiebung um  LE in positive y-Richtung („nach oben“) und um
LE in positive y-Richtung („nach oben“) und um  LE in negative x-Richtung („nach links“)
LE in negative x-Richtung („nach links“)
a)
b)
c)
d)
e)
f)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
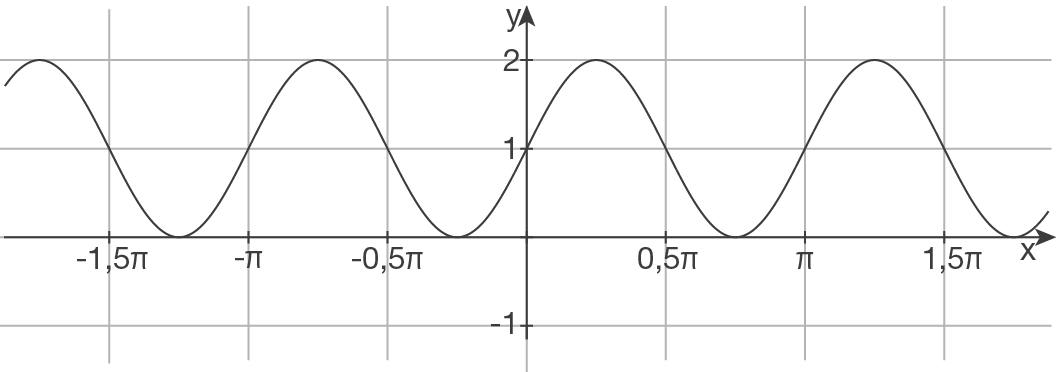
a)
Periode bestimmen
Um die Periode zu berechnen, benutze die Formel
Skizze
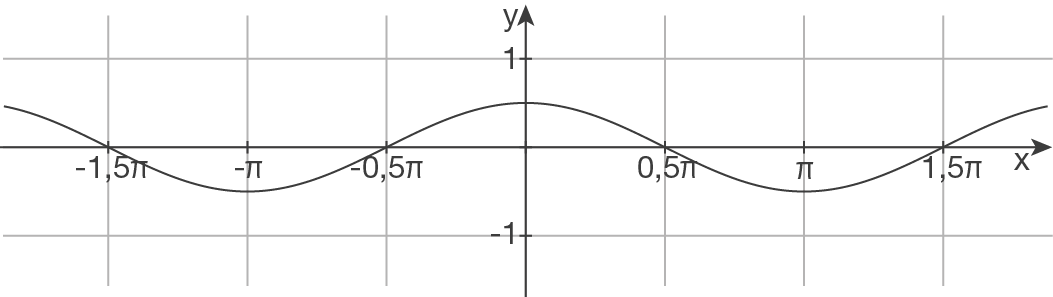
b)
Periode bestimmen
Skizze
c)
Periode bestimmen
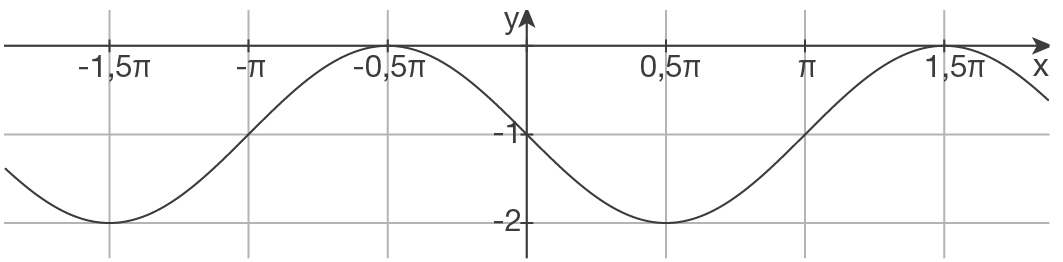
d)
Periode bestimmen
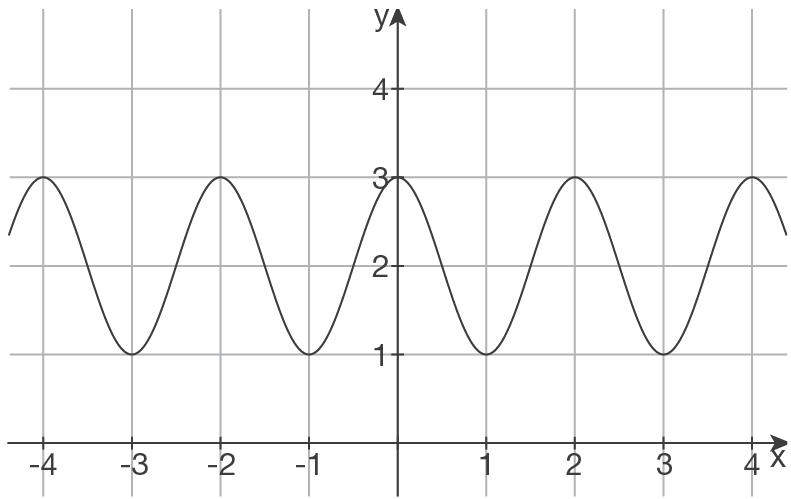
e)
Periode bestimmen
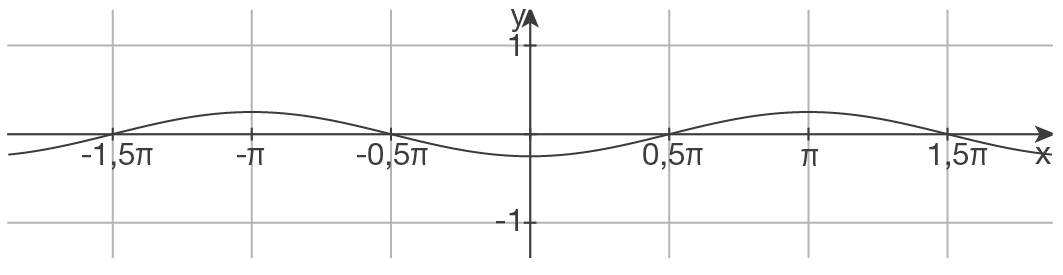
f)
Periode bestimmen
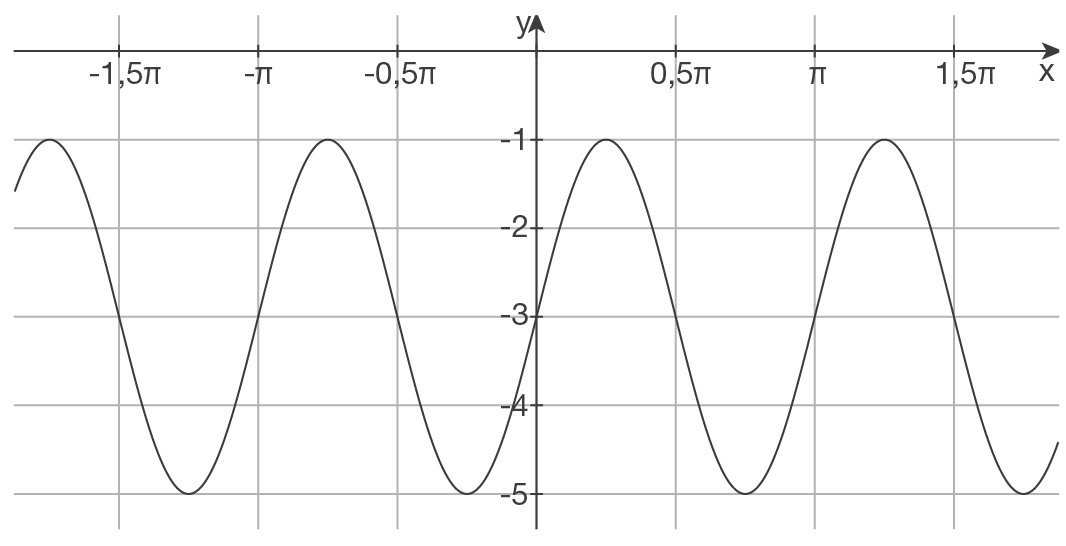
2.
a)
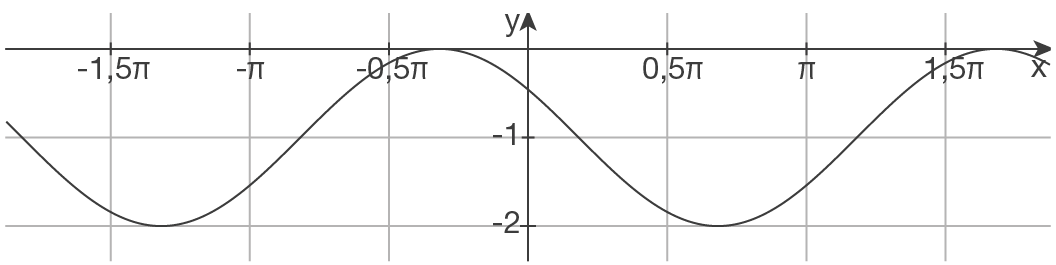
| a | Keine Streckung in |
| Periode |
|
| Verschiebung um |
|
| Verschiebung um 1 LE in negative |
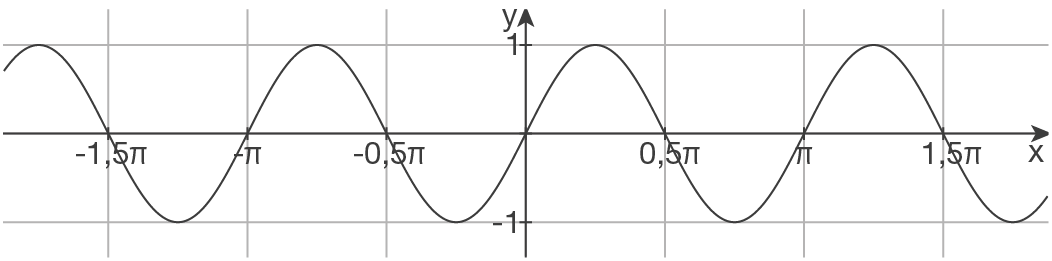
b)
Skizze
c)
Skizze
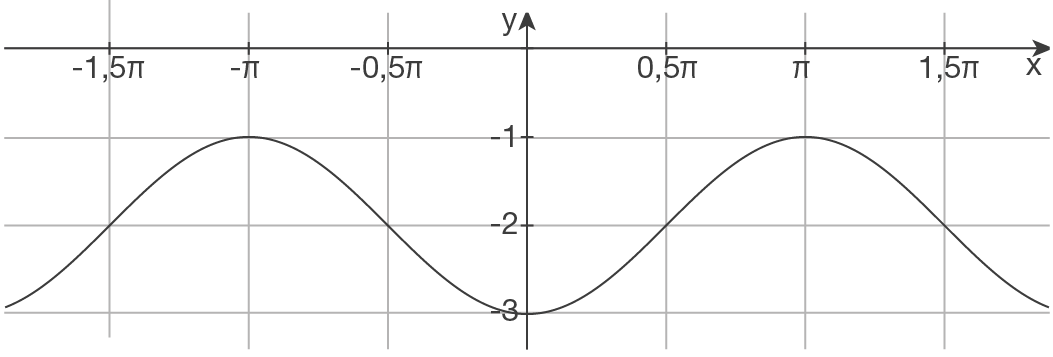
| Spiegelung an der |
|
| Periode |
|
| Verschiebung um 2 LE in negative |
d)
Skizze
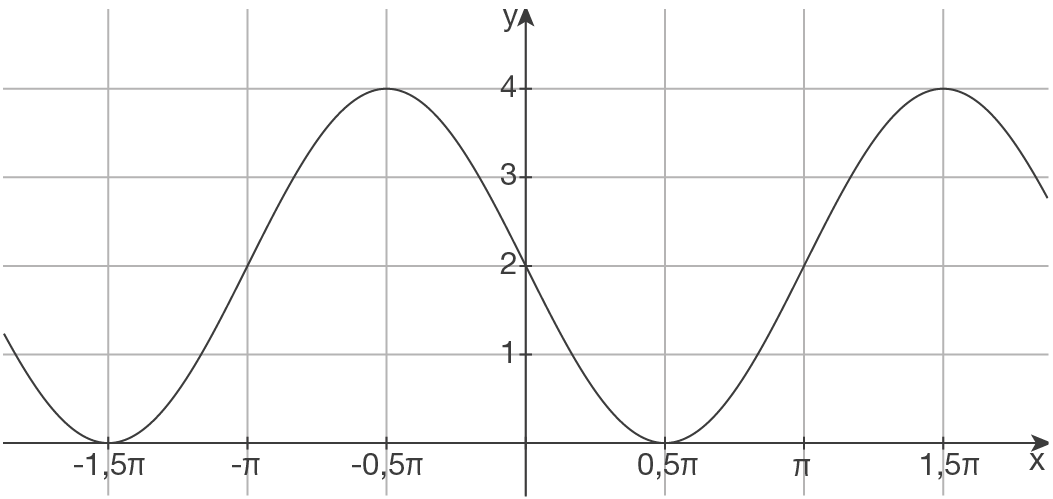
| Streckung um Faktor |
|
| Periode |
|
| Verschiebung um |
e)
Skizze
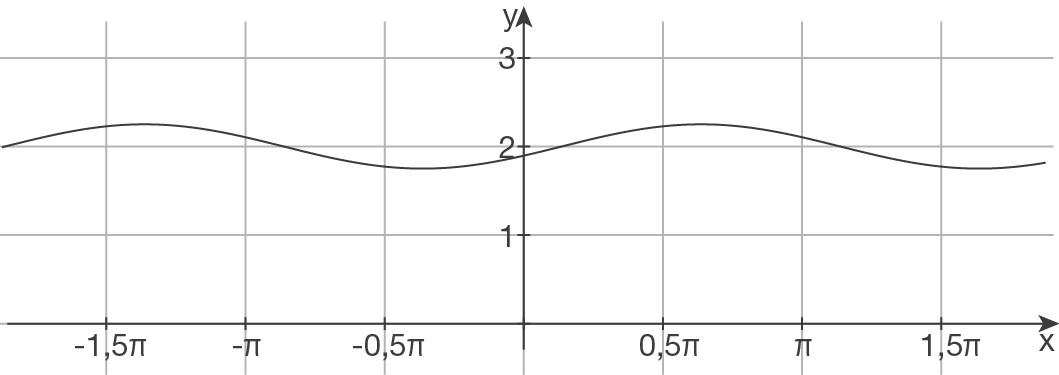
| Streckung um Faktor |
|
| Periode |
|
| Verschiebung um |
|
| Verschiebung um |
f)
Skizze

| Spiegelung an der |
|
| Periode |
|
| Verschiebung um |
|
| Verschiebung um |
3.
a)
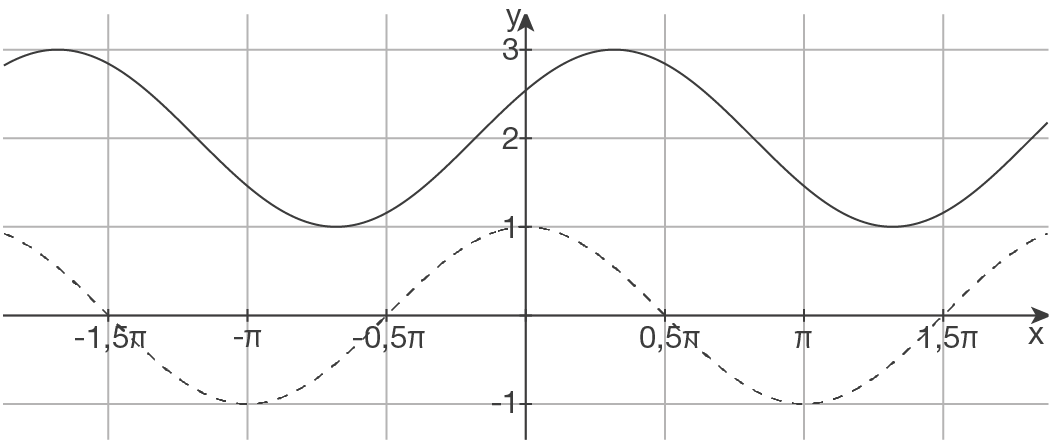
b)
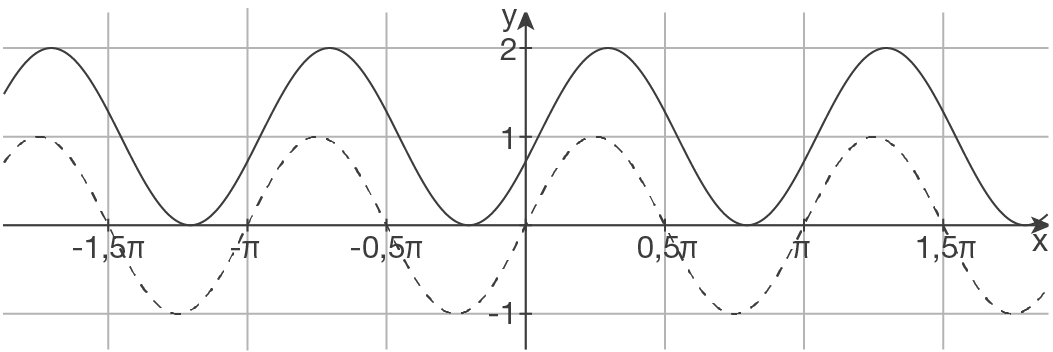
c)
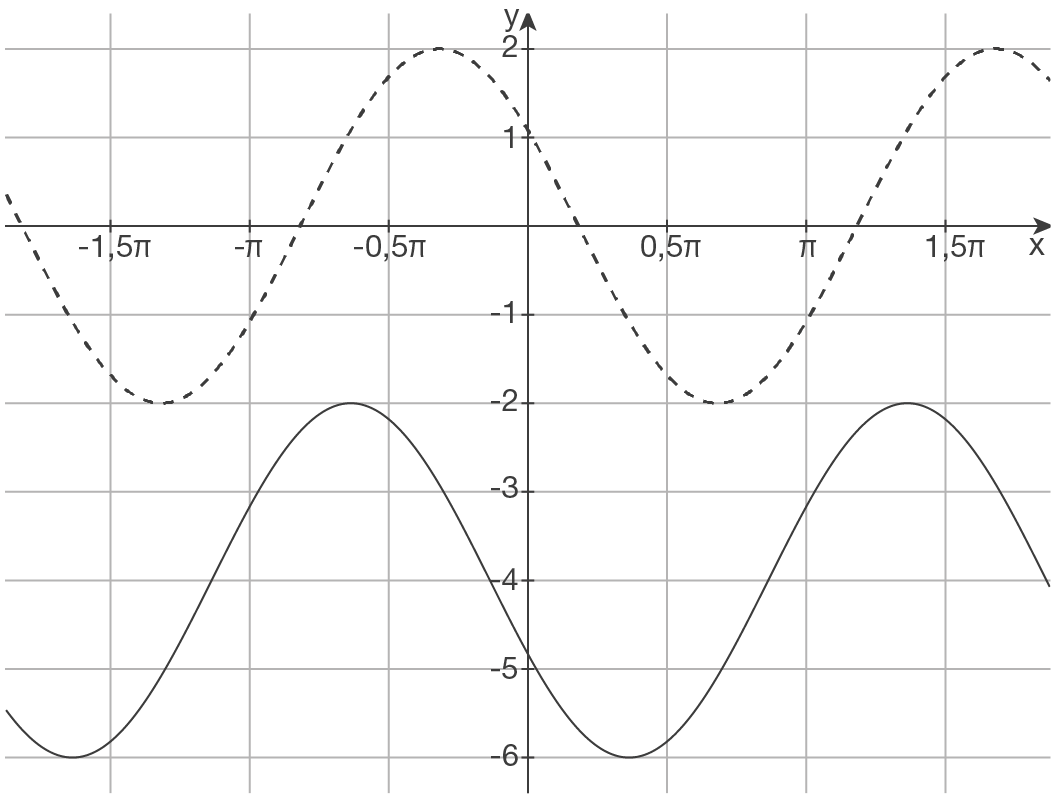
d)
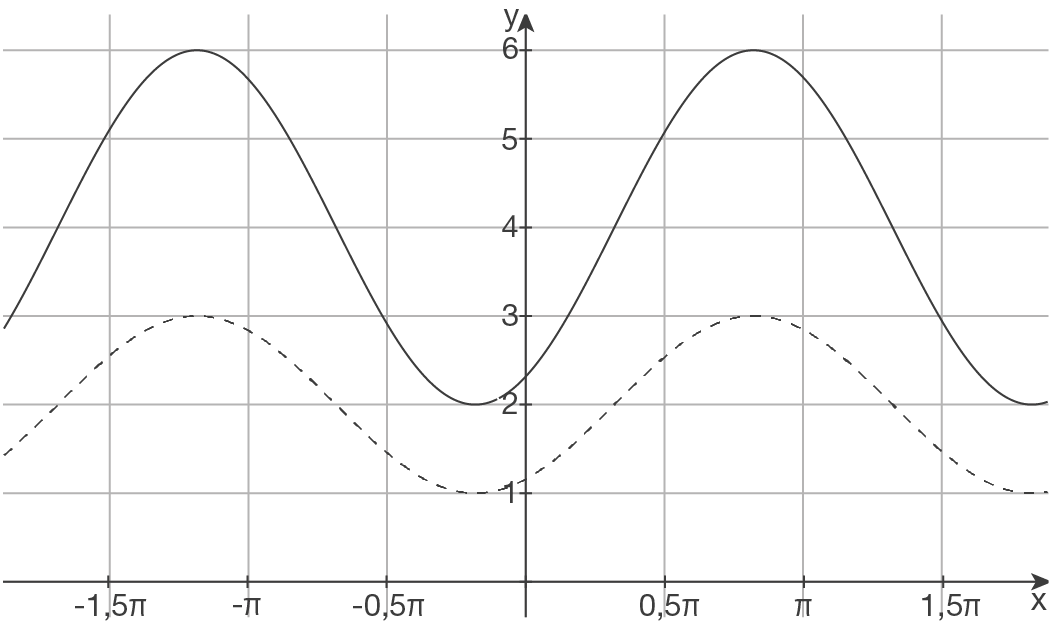
e)
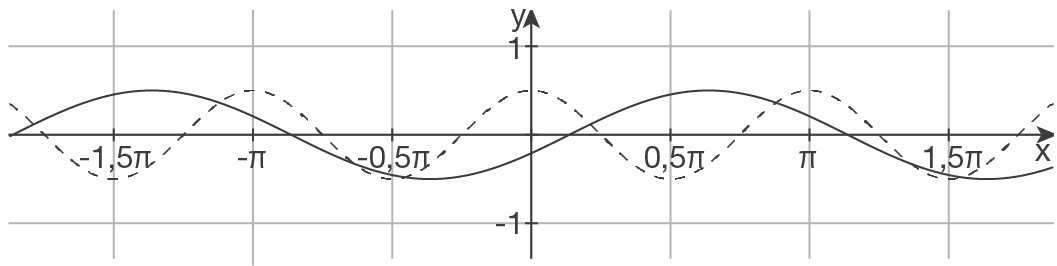
f)