Exponentialfunktionen
Exponentialfunktionen sind Funktionen der Form
 Sollst du hier eine Funktionsgleichung aufstellen, so hilft dir am besten das Ablesen der Koordinaten verschiedener Punkte, wähle dazu
Sollst du hier eine Funktionsgleichung aufstellen, so hilft dir am besten das Ablesen der Koordinaten verschiedener Punkte, wähle dazu  Punkte.
Punkte.
Hast du verschiedene Funktionsgleichungen gegeben und sollst auswählen, welche zu dem Graphen passt, so kannst du mit dem Graphen der -Funktion
-Funktion  vergleichen und so überlegen welche Parameterbelegung für
vergleichen und so überlegen welche Parameterbelegung für  ,
,  ,
,  und
und  am passendsten wäre.
am passendsten wäre.
Dabei können dir folgende Hinweise helfen:
Hast du verschiedene Funktionsgleichungen gegeben und sollst auswählen, welche zu dem Graphen passt, so kannst du mit dem Graphen der
Dabei können dir folgende Hinweise helfen:
- Ist der Graph der
-Funktion an der
-Achse gespiegelt, so muss
sein.
- Ist der Graph der
-Funktion an der
-Achse gespiegelt, so muss
sein.
- Ist der Graph entlang der
-Achse verschoben? Überprüfe dazu die waagerechte Asymptote: Der Graph zu
nähert sich für sehr kleine
-Werte immer mehr der Gerade zu
. Ist diese Asymptote verschoben, dann muss der Parameter
sein.
- Ist der Graph entlang der
-Achse verschoben? Für die
-Funktion gilt
. Ist dies hier nicht der Fall und der Graph auch nicht entlang der
-Achse verschoben, muss
sein.
- Ist der Graph gestreckt/gestaucht? Wächst bzw. fällt der Graph langsamer als der der
-Funktion, muss
oder
sein. Wächst bzw. fällt der Graph schneller als der der
-Funktion, muss
oder
sein.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
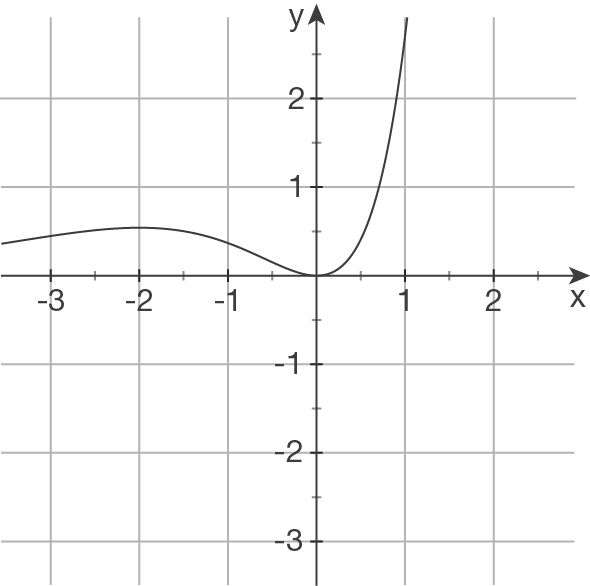
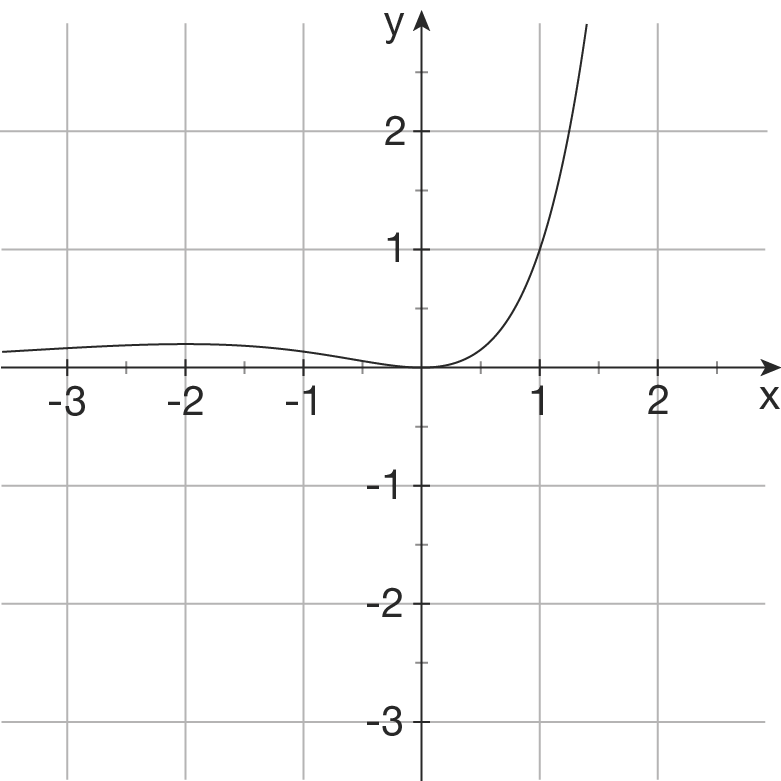
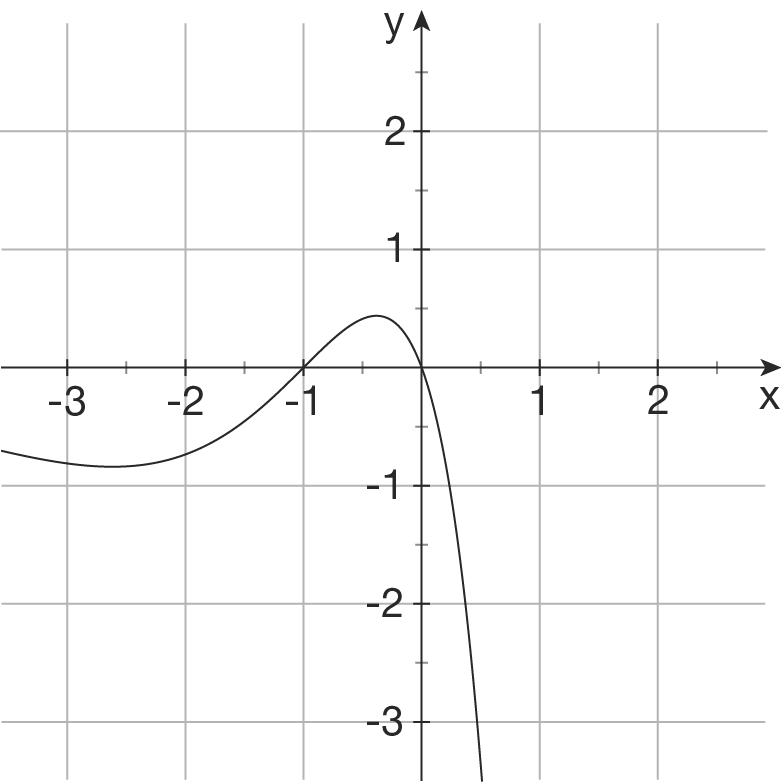
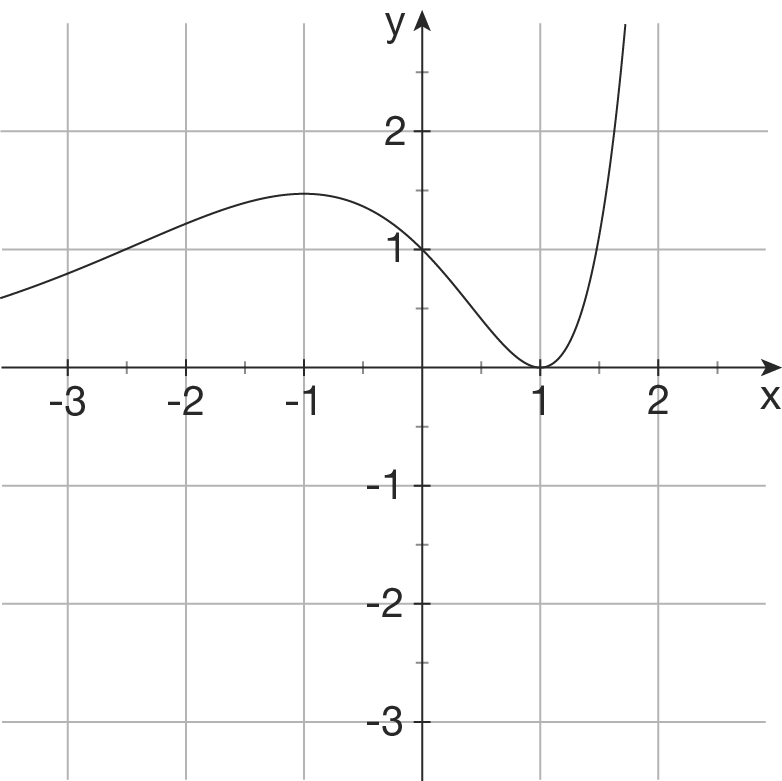
1.
Zuordnungen

 (4)
Begründung:
(4)
Begründung:  hat als einzige der vier Funktionen eine Nullstelle bei
hat als einzige der vier Funktionen eine Nullstelle bei  .
.

 (2)
Begründung:
(2)
Begründung:  , da
, da  . Weiterhin liegt
. Weiterhin liegt  auf keinem anderen Schaubild.
auf keinem anderen Schaubild.

 (1)
Begründung:
(1)
Begründung:  ist immer positiv, da
ist immer positiv, da  und
und  für alle
für alle  positiv sind. Da (2) und (4) bereits zugeordnet sind und (3) negative Werte annimmt, ist (1) die Lösung nach dem Ausschlussprinzip.
positiv sind. Da (2) und (4) bereits zugeordnet sind und (3) negative Werte annimmt, ist (1) die Lösung nach dem Ausschlussprinzip.

 (3)
Begründung:
(3)
Begründung:  besitzt als einziges Schaubild bei
besitzt als einziges Schaubild bei  und
und  Nullstellen.
Nullstellen.
a)
b)
c)
d)
2.
Zuordnungen

 (2)
Begründung:
(2)
Begründung:  besitzt als einziges Schaubild an
besitzt als einziges Schaubild an  eine Nullstelle. Der Punkt
eine Nullstelle. Der Punkt  liegt zudem nur auf dem Schaubild von (2).
liegt zudem nur auf dem Schaubild von (2).

 (3)
Begründung:
(3)
Begründung:  besitzt wie (1) eine Nullstelle bei
besitzt wie (1) eine Nullstelle bei  , allerdings kann das Schaubild von (3) auch negative Werte annehmen, da
, allerdings kann das Schaubild von (3) auch negative Werte annehmen, da  für
für  negativ ist (siehe Schaubild).
negativ ist (siehe Schaubild).

 (1)
Begründung:
(1)
Begründung:  ist immer positiv, da
ist immer positiv, da  und
und  für alle
für alle  positiv sind.
positiv sind.
a)
b)
c)