Trigonometrische Funktionen

Du kannst eine Trigonometrische Funktion auf folgende Eigenschaften überprüfen.
Beachte, dass eine trigonometrische Funktion eine periodische Funktion ist und es daher evtl. unendlich viele Nullstellen, Extrempunkte und Wendepunkte gibt.

Eigenschaft	Methode
Schnittpunkte mit den Koordinatenachsen $(x_0\mid y_0)$	x-Achse: Nullstelle bestimmen, d.h. $y_0 = 0$ , setze also $f(x_0)=0$ und löse nach $x_0$ auf y-Achse: Funktionswert an der Stelle $x_0 = 0$ berechnen, also $y_0 = f(0)$
Extrempunkt $(x_E\mid y_E)$	Notwendiges Kriterium: $f‘(x_E)=0$ Hinreichendes Kriterium: Hochpunkt: $f‘‘(x_E) \lt 0$ oder Vorzeichenwechsel von $f‘(x)$ in $x_E$ von $+$ nach $-$ Tiefpunkt: $f‘‘(x_E) \gt 0$ oder Vorzeichenwechsel von $f‘(x)$ in $x_E$ von $-$ nach $+$
Wendepunkt $(x_W\mid y_W)$	Notwendiges Kriterium: $f‘‘(x_W)=0$ Hinreichendes Kriterium: $f‘‘‘(x_W) \neq 0$ oder Vorzeichenwechsel von $f‘‘(x)$ in $x_W$
Graph skizzieren	Verwende zum Skizzieren markante Stellen z.B. Nullstellen, Hochpunkte, usw.
Symmetrie	achsensymmetrisch: $f(x)=f(-x)$ punktsymmetrisch: $-f(x)=f(-x)$

$f\left(x\right)=\sin{\left(2x\right)}$

Schnittpunkte mit der $\boldsymbol{x}$ -Achse bestimmen: $\boldsymbol{f\left(x\right)=0}$ setzen und nach $\boldsymbol{x}$ auflösen

$\begin{array}{rllll} \sin{\left(2x\right)}&=0& \end{array}$

Vollständige Lösung anzeigen

Resubstitution:

$\begin{array}{rllrllrll} z_1&=-\pi&\scriptsize{\mid\;z=2x}\\[3pt] 2x&=-\pi&\scriptsize{\mid\;:2}\\[3pt] x_1&=-\dfrac{\pi}{2} \end{array}$

Vollständige Lösung anzeigen

Daraus ergeben sich die Punkte $N_1\left(-\dfrac{\pi}{2}\middle|0\right)$ , $N_2\left(0\middle|0\right)$ und $N_3\left(\dfrac{\pi}{2}\middle|0\right)$ .

Schnittpunkte mit der $\boldsymbol{y}$ -Achse bestimmen: $\boldsymbol{x=0}$ setzen und ausrechnen:

$\sin{\left(2\cdot0\right)}=0$

Daraus ergibt sich der Punkt $P\left(0\middle|0\right)$ .

Extrema bestimmen

Ableitungen bilden

$\begin{array}{rlll} f\left(x\right)&=\sin{\left(2x\right)}\\[3pt] f‘\left(x\right)&=2\cos{\left(2x\right)}\\[3pt] f‘‘\left(x\right)&=-4\sin{\left(2x\right)} \end{array}$

$f‘\left(x\right)=0$ setzen

$\begin{array}{rllll} z_2&=\dfrac{\pi}{2} \end{array}$

Vollständige Lösung anzeigen

Resubstitution:

$\begin{array}{rllrll} z_1&=-\dfrac{\pi}{2}&\scriptsize{\mid\;z=2x}\\[5pt] 2x&=-\dfrac{\pi}{2}&\scriptsize{\mid\;:2}\\[5pt] x_1&=-\dfrac{\pi}{4} \end{array}$

Vollständige Lösung anzeigen

Hochpunkt oder Tiefpunkt?
$x=-\dfrac{\pi}{4}$ und $x=-\dfrac{\pi}{4}$ in $f‘‘\left(x\right)$ einsetzen

$\begin{array}{rllll} f‘‘\left(-\dfrac{\pi}{4}\right)&=-4\sin\;... \end{array}$

Vollständige Lösung anzeigen

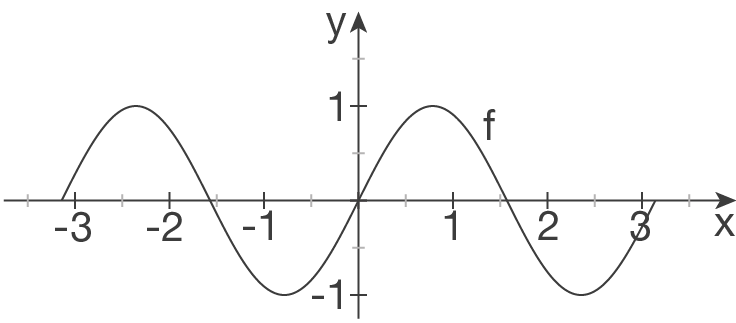
Graph einer sinusförmigen Funktion mit Achsenbeschriftungen.

Nachweisen, dass $\boldsymbol{W}$ ein Wendepunkt ist

Ableitungen bilden

$\begin{array}{rlll} f\left(x\right)&=\sin{\left(2x\right)}\\[3pt] f‘\left(x\right)&=2\cos{\left(2x\right)}\\[3pt] f‘‘\left(x\right)&=-4\sin{\left(2x\right)}\\[3pt] f‘‘‘\left(x\right)&=-8\cos{\left(2x\right)} \end{array}$

$W$ ist ein Wendepunkt von $K_f$ , wenn notwendiges und hinreichendes Kriterium erfüllt sind, d.h. wenn gilt: $f‘‘(0)=0$ und $f‘‘‘(0)\neq0$ .

$f‘‘\left(0\right)$ und $f‘‘‘(0)$ ausrechnen

$\begin{array}{rllll} f‘‘\left(0\right)&=-4\sin{\left(2\cdot0\right)}\\[3pt] &=-4\cdot0\\[3pt] f‘‘\left(0\right)&=0\\[6pt] f‘‘‘(0)&=-8\cdot\cos(2\cdot0)\\[3pt] &=-8\cdot1\\[3pt] f‘‘‘(0)&=-8\neq0 \end{array}$

Es handelt sich um einen Wendepunkt.

Punktsymmetrie zum Wendepunkt nachweisen

Zu zeigen:

$f\left(x\right)=-f\left(-x\right)$

Beweis:

$\sin{\left(2x\right)}=-\sin{\left(-2x\right)}$

Dies ist eine wahre Aussage, da die Sinus-Funktion generell punktsymmetrisch ist. Die Gleichung, die hier steht, spiegelt diese Punktsymmetrie wieder.

Funktionsgraphen strecken

Um die Amplitudenhöhe zu beeinflussen, wird ein Koeffizient vor den Sinus gestellt:

$a\cdot\sin{\left(2x\right)}$

Für $a>1$ wird die Funktion gestreckt.
Für $0\lt a\lt 1$ wird die Funktion gestaucht.

$f\left(x\right)=3\cos{\left(x-\pi\right)}$

Schnittpunkte mit der $\boldsymbol{x}$ -Achse bestimmen: $\boldsymbol{f\left(x\right)=0}$ setzen und nach $\boldsymbol{x}$ auflösen

$\begin{array}{rllll} 3\cos{\left(x-\pi\right)}&=0&\scriptsize{\mid\;:3} \end{array}$

Vollständige Lösung anzeigen

Resubstitution:

$\begin{array}{rllrllrll} z_{1}&=-\dfrac{3}{2}\pi&\scriptsize{\mid\;z=x-\pi}\\[5pt] x-\pi&=-\dfrac{3}{2}\pi&\scriptsize{\mid\;+\pi}\\[5pt] x_{1}&=-\dfrac{1}{2}\pi& \end{array}$

Vollständige Lösung anzeigen

Daraus ergeben sich die Punkte $N_1\left(-\dfrac{1}{2}\pi\middle|0\right)$ und $N_2\left(\dfrac{1}{2}\pi\middle|0\right)$ .

Schnittpunkte mit der $\boldsymbol{y}$ -Achse bestimmen: $\boldsymbol{x=0}$ setzen und ausrechnen:

$\begin{array}{rllll} f\left(0\right)&=3\cos{\left(0-\pi\right)}\\[3pt] f\left(0\right)&=3\cdot\left(-1\right)\\[3pt] f\left(0\right)&=-3 \end{array}$

Daraus ergibt sich der Punkt $P\left(0\middle|-3\right)$ .

Extrema bestimmen

Ableitungen bilden

$\begin{array}{rlll} f\left(x\right)&=3\cos{\left(x-\pi\right)}\\[3pt] f‘\left(x\right)&=-3\sin{\left(x-\pi\right)}\\[3pt] f‘‘\left(x\right)&=-3\cos{\left(x-\pi\right)} \end{array}$

$f‘\left(x\right)=0$ setzen

$\begin{array}{rllll} z_1&=-2\pi\\[3pt] z_2&=-\pi\\[3pt] z_3&=0 \end{array}$

Vollständige Lösung anzeigen

Resubstitution:

$\begin{array}{rllrllrll} z_{1}&=-2\pi&\scriptsize{\mid\;z=x-\pi}&\\[3pt] x-\pi&=-2\pi&\scriptsize{\mid\;+\pi}&\\[3pt] x_{1}&=-\pi& \end{array}$

Vollständige Lösung anzeigen

Hochpunkt oder Tiefpunkt? $x=-\pi$ , $x=0$ und $x=\pi$ in $f‘‘\left(x\right)$ einsetzen

$\begin{array}{rllll} f‘‘\left(-\pi\right)&=-3\cos{\left(-\pi-\pi\right)}\\[3pt] &=-3\cos{\left(-2\pi\right)}\\[3pt] &=-3, \scriptsize{\lt 0: \text{Maximum}}\\[6pt] f‘‘\left(0\right)&=-3\cos{\left(0-\pi\right)}\\[3pt] &=-3\left(-1\right)\\[3pt] &=3, \scriptsize{>0, \text{Minimum}}\\[6pt] f‘‘\left(\pi\right)&=-3\cos{\left(\pi-\pi\right)}\\[3pt] &=-3\cos{\left(0\right)}\\[3pt] &=-3, \scriptsize{\lt 0, \text{Maximum}} \end{array}$

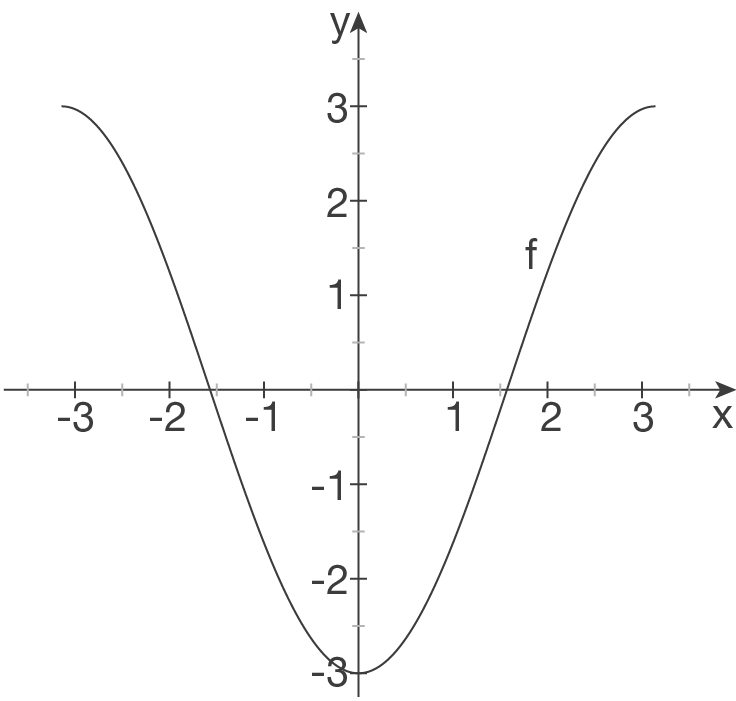
Graph einer Parabel mit der Funktion f, dargestellt im xy-Koordinatensystem.

Symmetrieachse finden

Eine mögliche Symmetrieachse wäre die $y$ -Achse:

Behauptung:

$K_f$ ist achsensymmetrisch zu $x=0$

Zu zeigen:

$f\left(x\right)=$ & $f\left(-x\right)$

Beweis:

$3\cos{\left(x-\pi\right)}=$ & $3\cos{\left(-x-\pi\right)}$

Dies ist eine wahre Aussage.
Die Kosinusfunktion verläuft immer regelmäßig und achsensymmetrisch zur $y$ -Achse. Somit gilt für den Kosinus immer $f\left(x\right)=f\left(-x\right)$ .

Wenn nun, wie in unserem Beispiel, von jeder Zahl das Gleiche abgezogen wird, verändert sich der Abstand der beiden Stellen nicht, weil beide um den gleichen Abstand verschoben werden. Somit stimmen auch die $y$ -Werte überein.

Verschiebung in $\boldsymbol{x}$ -Richtung

Um das Schaubild der Funktion in $x$ -Richtung (also links oder rechts) zu verschieben, muss direkt hinter dem $x$ eingegriffen werden. Dies lässt sich leicht am Beispiel der Normalparabel verdeutlichen:

$y=x^2\\ \scriptsize{\text{Parabel läuft durch} P\left(0\middle|0\right)}\\[3pt] y=\left(x-1\right)^2\\ \scriptsize{\text{Parabel läuft durch} P\left(1\middle|0\right)\\\text{Verschiebung in pos. x-Richtung}}\\[3pt] y=\left(x+1\right)^2\\ \scriptsize{\text{Parabel läuft durch} P\left(-1\middle|0\right)\\\text{Verschiebung in neg. x-Richtung}}$

Somit lässt sich die Kosinusfunktion wie folgt verschieben:

$f\left(x\right)=3\cos{\left(x-a-\pi\right)}$ .

Verschiebung in $\boldsymbol{y}$ -Richtung

Um das Schaubild der Funktion in $y$ -Richtung (also oben oder unten) zu verschieben, muss hinter dem Term eingegriffen werden. Dies lässt sich auch leicht am Beispiel der Normalparabel verdeutlichen:

$y=x^2\\\scriptsize{\text{Parabel läuft durch} P\left(0\middle|0\right)}\\[3pt] y=\left(x\right)^2+1\\\scriptsize{\text{Parabel läuft durch} P\left(0\middle|1\right)\\ \text{Verschiebung in pos. y-Richtung}}\\[3pt] y=\left(x\right)^2-1\\\scriptsize{\text{Parabel läuft durch} P\left(0\middle|-1\right)\\ \text{Verschiebung in neg. y-Richtung}}$

Somit lässt sich die Kosinusfunktion wie folgt verschieben:

$f\left(x\right)=3\cos{\left(x-\pi\right)}-a$ .

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?