Binomialverteilung Tabelle
Um für eine binomialverteilte Zufallsvariable 
Wahrscheinlichkeiten der Form 
zu berechnen, gibt es die Tabellen zur kumulierten Binomialverteilung.
, wobei 
binomialverteilt ist mit den Parametern 
und 
. Du betrachtest die Spalte zu und die Zeile zu 
. Du musst die untere graue Tabellenbeschriftung betrachten, und das Ergebnis anschließend von 
abziehen:
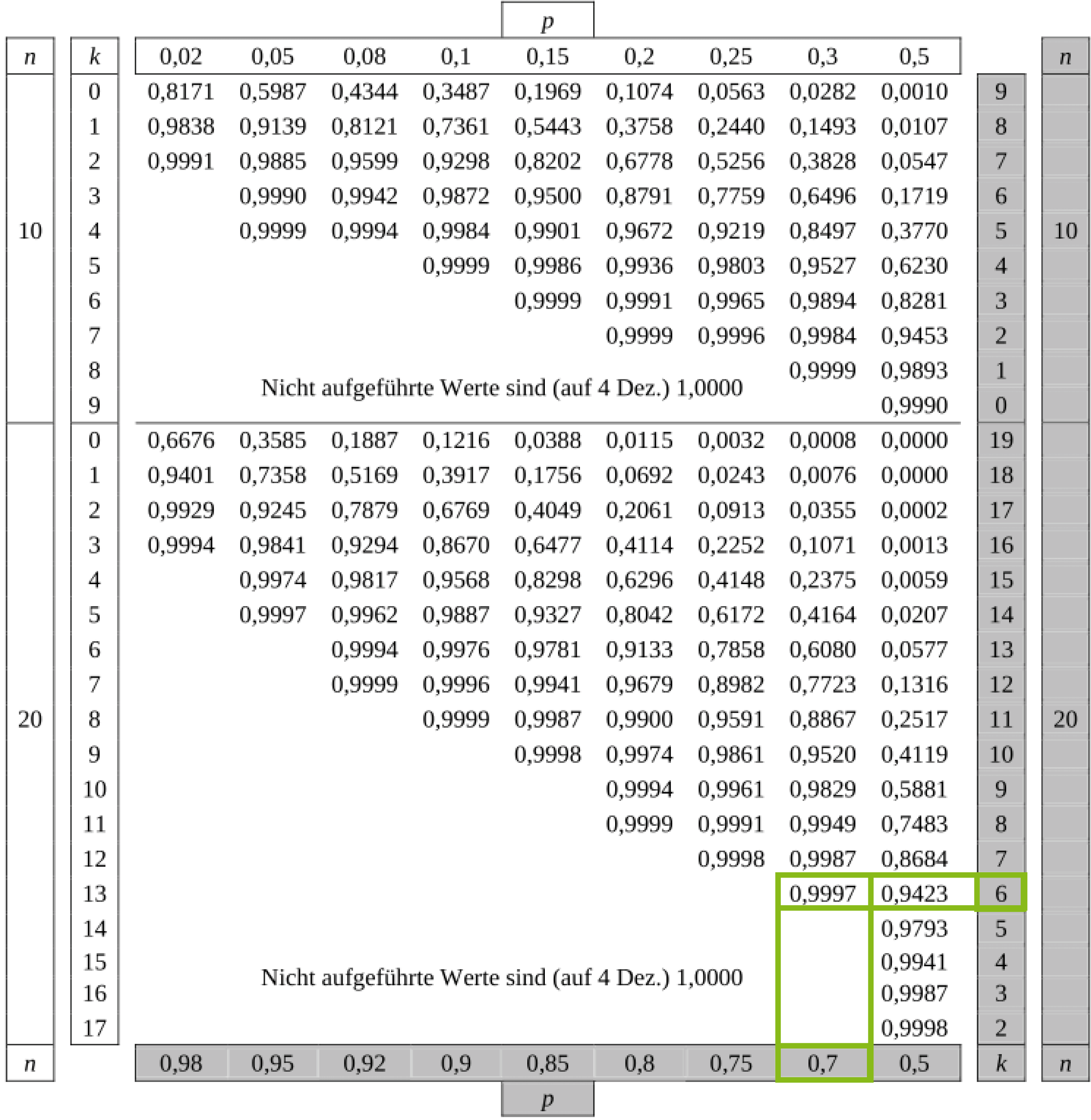Die gesuchte Wahrscheinlichkeit beträgt 
.
Vorgehen
- Wähle die zum Stichprobenumfang
der Binomialverteilung passende Tabelle.
- Wähle die Spalte zur passenden Wahrscheinlichkeit
. Ist
, musst du die grau unterlegten Spalten- und Zeilenbezeichnungen im unteren Teil der Tabelle betrachten.
- Lies den Wert in der entsprechenden Zeile zu
ab. Ist
Tabelleneintrag, sonst ist das Ergebnis einfach der Tabelleneintrag.
Beispiel
Wir suchen die Wahrscheinlichkeit
1.
Bestimme für 
und 
die folgenden Wahrscheinlichkeiten.
a)
b)
c)
d)
e)
f)
2.
Bestimme für 
und 
die folgenden Wahrscheinlichkeiten.
a)
b)
c)
d)
e)
f)
3.
Bestimme jeweils die gesuchte Wahrscheinlichkeit.
a)
b)
c)
4.
Eine Münze wird 50-mal geworfen.
Wie groß ist die Wahrscheinlichkeit für folgende Ereignisse?
Es fällt höchstens 
-mal „Wappen“
Es fällt mehr als -mal „Wappen“
Es fällt genau 
-mal „Wappen“
Es werden mindestens 17 und höchstens 35 „Wappen“ geworfen.
Es werden mehr als und weniger als 
„Wappen“ geworfen.
Wie groß ist die Wahrscheinlichkeit für folgende Ereignisse?
a)
b)
c)
d)
e)
5.
Ein Glücksrad ist unterteilt in fünf gleich große Sektoren (nummeriert von 1-5). Es wird 
-mal gedreht. Wie groß ist die Wahrscheinlichkeit für folgende Ereignisse?
Das Glücksrad hält höchstens -mal im Sektor 5 an.
Das Glückrad hält mindestens 
-mal aber höchstens 
-mal im Sektor 3.
Das Glücksrad hält höchstens 
-mal bei einem Sektor mit ungerader Zahl.
a)
b)
c)
6.
Bestimme die Wahrscheinlichkeit, dass sich unter
Wie groß ist die Wahrscheinlichkeit, dass sich unter den
7.
Im Rahmen einer Marketing-Analyse wurden Passanten nach ihrer Meinung zu einer Werbe-Anzeige befragt. Das Ergebnis war, dass 
der befragten Personen die Werbe-Anzeige gut fanden.
Dieses Ergebnis soll nun in einer Stichprobe von
Personen geprüft werden. Ermittle, wie viele der befragten Personen die Werbe-Anzeige gut finden müssen, damit die Hypothese „ der befragten Personen finden die Werbe-Anzeige gut“ mit einer Wahrscheinlichkeit von mindestens 
stimmt.
Dieses Ergebnis soll nun in einer Stichprobe von
8.
In einer Firma werden Prozessorchips produziert. Die Chips werden unabhängig voneinander hergestellt. Die Wahrscheinlichkeit für einen nicht funktionierenden Chip liegt bei 
.
Der Produktion wird eine Stichprobe von Chips entnommen.
Berechne die Wahrscheinlichkeit, mit der zehn Chips nicht funktionieren.
Wie groß ist die Wahrscheinlichkeit, dass mehr als drei Chips fehlerhaft sind?
Berechne den Umfang einer Stichprobe, wenn in dieser mit einer Wahrscheinlichkeit von mindestens
mindestens ein nicht funktionierender Chip enthalten sein soll.
Der Produktion wird eine Stichprobe von
Berechne die Wahrscheinlichkeit, mit der zehn Chips nicht funktionieren.
Wie groß ist die Wahrscheinlichkeit, dass mehr als drei Chips fehlerhaft sind?
Berechne den Umfang einer Stichprobe, wenn in dieser mit einer Wahrscheinlichkeit von mindestens
9.
Die alljährliche Generalversammlung des Karnickelzüchtervereins „Hasenpfote“ steht kurz bevor. Zu der Generalversammlung sind die 
Mitglieder eingeladen. Die langjährige Erfahrung des 1. Vorsitzenden Herr Hasenfuß haben aber gezeigt, dass nur 
der Mitglieder kommen.
a)
Mit welcher Wahrscheinlichkeit kommen mehr als 
Mitglieder zur Generalversammlung?
b)
Der Verein soll von dem Namen „Hasenpfote“ zu „Falscher Hase“ umbenannt werden. Dies geht laut Satzung nur, wenn mehr als 
der Mitglieder anwesend sind. Wie viele Generalversammlungen sind daher mindestens nötig, um mit einer Wahrscheinlichkeit von eine Namensänderung des Vereins möglich zu machen?
10.
Ein cleverer Reiseveranstalter weiß, dass im Durchschnitt seiner Buchungen storniert werden. Er verkauft daher 200 Reisen, obwohl er nur 190 zur Verfügung hat.
a)
Gib einen Term 
an, der beschreibt, mit welcher Wahrscheinlichkeit genau 
der Buchungen storniert werden.
Für welches ist diese Wahrscheinlichkeit am größten?
Für welches
b)
Mit welcher Wahrscheinlichkeit reichen die Reisen nicht aus?
c)
Am Abreisetag wollen nun 
Personen ihre Reise antreten. Der Reiseanbieter muss also 
Personen noch eine Reise gewährleisten. Diese muss er teuer bei einem anderen Reiseveranstalter einkaufen. Eine Fußballmannschaft ( Spieler) tritt nun zum besagten Abreisetag ihre Reise nach Mallorca an. Mit welcher Wahrscheinlichkeit reisen genau zwei Fußballer mit einem anderen Reiseanbieter?
11.
Aufgrund langjähriger Erfahrung behauptet ein Autoverkäufer, dass er Autos mit einer Wahrscheinlichkeit von verkauft. Es kommen Kunden in sein Autohaus.
aber weniger als 
Autos verkauft wurden.
mindestens verkauft werden.
a)
Berechne den Erwartungswert an verkauften Autos.
b)
Berechne die Wahrscheinlichkeit, dass mindestens
c)
Ermittle, wie viele Autos mit einer Wahrscheinlichkeit von mehr als
12.
Eine bekannte Firma stellt Pommes her. 
aller hergestellten Pommes entsprechen nicht der Norm und werden aussortiert. Die Firma beauftragt nun ein externes Expertenteam, welches die Qualität verbessern soll. Ziel ist es, einen Ausschluss von unter zu erreichen. Gelingt dies dem Expertenteam, so wird ihm eine satte Prämie bezahlt.
Zur Kontrolle des Expertenteams entnimmt die Firma nach erledigter Arbeit eine Stichprobe von Pommes. Befinden sich in dieser nicht mehr als 
Fehlerhafte, so hat sich das Expertenteam die Prämie verdient.
Zur Kontrolle des Expertenteams entnimmt die Firma nach erledigter Arbeit eine Stichprobe von
a)
Mit welcher Wahrscheinlichkeit erhält das Team die Prämie, obwohl keine Qualitätsverbesserung eingetreten ist?
b)
Mit welcher Wahrscheinlichkeit wird dem Team die Prämie verweigert, obwohl der Anteil der aussortierten Pommes unter 
gesunken ist?
13.
Ein IT-Fachmarkt will um jeden Preis, dass mindestens der Bevölkerung sein Angebot kennen. Nun wird eine wirksame Werbekampagne eingeleitet. Ob störende TV-Spots oder auffällige Anzeigen, es wird kein Mittel gescheut. Zwei Wochen nach Start der Werbekampagne wird nun ein erstes Resumee gezogen.
Es wird eine Umfrage mit zufällig ausgewählten Personen durchgeführt. Bestimme die Anzahl der Personen, die den IT-Fachmarkt aufgrund der Werbekampagne mit einer Wahrscheinlichkeit von mindestens kennen sollte.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
In einer Tabelle für die aufsummierte Binomialverteilung kann man die Wahrscheinlichkeit 
ablesen. Ablesen aus der Tabelle für und führt zu:
a)
b)
Vollständige Lösung anzeigen
c)
d)
e)
f)
2.
In einer Tabelle für die aufsummierte Binomialverteilung, kann man die Wahrscheinlichkeit ablesen. Es gilt und .
a)
b)
c)
d)
e)
f)
3.
4.
Beim Wurf einer Münze gibt es zwei mögliche Ergebnisse: „Wappen“ oder „Zahl“. Beide Ergebnisse treten mit der gleichen Wahrscheinlichkeit auf, nämlich jeweils mit 
. In einer Tabelle für die aufsummierte Binomialverteilung, kann man die Wahrscheinlichkeit ablesen. Es gilt 
und .
a)
„Höchstens Mal“ bedeutet Mal und weniger. Sei die Anzahl der geworfenen „Wappen“:
b)
c)
d)
e)
5.
Die fünf Sektoren sind gleich groß. Damit wird jeder Sektor mit der gleichen Wahrscheinlichkeit von 
gedreht. In einer Tabelle für die aufsummierte Binomialverteilung kannst du die Wahrscheinlichkeit ablesen. Es gilt und 
.
a)
b)
c)
Die Sektoren sind von bis durchnummeriert. Mögliche Sektoren sind also die mit den Nummern , 
und . Bei einem solchen Zufallsversuch, bei dem sich das Ergebnis aus mehreren Möglichkeiten zusammensetzt, berechnest du die Wahrscheinlichkeit mit der Summenregel.
Da jeder der drei Sektoren mit einer Wahrscheinlichkeit von gedreht wird, ergibt sich für das Ereignis „Ein Sektor mit ungerader Zahl wird gedreht“ eine Wahrscheinlichkeit von 
.
Da jeder der drei Sektoren mit einer Wahrscheinlichkeit von
6.
Die Zufallsgröße beschreibe die Anzahl der erkrankten Personen (in der Stichprobe ). Wir gehen davon aus, dass die Zufallsgröße binomialverteilt ist mit und 
.
Die Wahrscheinlichkeit, dass unter Personen genau 
Erkrankte sind beträgt somit:
Die Wahrscheinlichkeit, dass sich unter den mindestens fünf Kranke befinden, ist
7.
Die Zufallsgröße 
beschreibe die Anzahl der Befragten, welche die Werbeanzeige gut finden.
Da von der Hypothese „ der Befragten finden die Werbe-Anzeige gut“ ausgegangen wird, ist binomialverteilt mit 
und 
. Berechnet werden soll nun die Mindestanzahl der Befragten, welche die Werbe-Anzeige gut finen, sodass die Hypothese 
mit einer Wahrscheinlichkeit von mindestens eingehalten wird.
Schaut man in einer geeigneten Tabelle nach, so ist 
und 
.
Also ist
und damit 
. Es müssen mindestens 40 der Befragten die Werbeanzeige gelungen finden, so dass mit einer Wahrscheinlichkeit von mindestens die Marktanalyse von korrekt ist.
Da von der Hypothese „
Also ist
8.
Die Zufallsgröße beschreibe die Anzahl der fehlerhaften Chips (in der Stichprobe).
Die Zufallsgröße ist binomialverteilt mit und 
.
10 Chips funktionieren nicht:
Mehr als drei Chips sind fehlerhaft:
Berechnen des Mindestumfangs der Stichprobe (Mindestlänge einer Bernoulli-Kette):
Die Zufallsgröße
steht für die Anzahl der fehlerhaften Chips in einer Stichprobe mit dem Umfang .
Die Zufallsgröße ist binomialverteilt mit unbekannt und .
Wir suchen also ein mit 
Die Stichprobe muss mindestens 59 Chips umfassen.
Die Zufallsgröße
Berechnen des Mindestumfangs
Die Zufallsgröße
Die Zufallsgröße
Wir suchen also ein
9.
a)
| siehe Tafelwerk (kumulative Tabelle) oder GTR/CAS | |
b)
10.
a)
Sei die Zufallsvariable, die die Anzahl der stornierten Buchungen angibt. Dann ist binomialverteilt mit und .
Es ergibt sich
Schaut man sich die Tabelle der Binomialverteilung für und an, so kann man folgendes ablesen:
Somit haben wir durch Probieren, dass Maximum
gefunden. Die Wahrscheinlichkeit ist für genau 10 stornierte Buchungen am größten.
Somit haben wir durch Probieren, dass Maximum
b)
Da der Reiseanbieter nur 
Reisen zur Verfügung hat, müssen mindestens 
Personen ihre Reise stornieren. Sind es nur 9 oder weniger, hat der Reiseanbieter eine Doppelbuchung. sei die Zufallsvariable, die die Anzahl der stornierten Reisen beschreibt. sei binomialverteilt mit und .
c)
Die 195 Personen setzen sich zusammen aus 175 „Nicht-Fußballern“ und 20 „Fußballern“. 5 dieser 195 Personen müssen mit einem anderen Reiseanbieter reisen. Es soll die Wahrscheinlichkeit dafür bestimmt werden, dass genau 2 dieser fünf Personen Fußballer sind.
Es gibt insgesamt 
mögliche Zusammenstellungen von 5-er Gruppen. Günstig sind aber nur die, bei denen drei Nicht-Fußballer und zwei Fußballer ausgewählt werden. Für diese Kombination gibt es 
Möglichkeiten.
Für die gesuchte Wahrscheinlichkeit gilt damit:
Mit einer Wahrscheinlichkeit von etwa 
reisen genau zwei Fußballer mit einem anderen Reiseanbieter.
11.
Sei die Zufallsgröße, die die Anzahl der verkauften Autos beschreibt. Wir gehen von einer binomialverteilung von aus mit und 
.
a)
Erwartungswert:
Erwartungsgemäß verkauft er 40 der 50 Autos.
Erwartungsgemäß verkauft er 40 der 50 Autos.
b)
Sei A das Ereignis: „mindestens 40, aber weniger als 45 verkaufte Autos.“
Zu berechnen ist:
(siehe Tabellenwerte) Die Wahrscheinlichkeit dafür, dass mindestens 40 aber weniger als 45 Autos verkauft wurden, beträgt
.
Zu berechnen ist:
(siehe Tabellenwerte) Die Wahrscheinlichkeit dafür, dass mindestens 40 aber weniger als 45 Autos verkauft wurden, beträgt
c)
Gesucht ist die Anzahl der Autos, die mit einer Wahrscheinlichkeit von mehr als mindestens verkauft werden. Sei die Anzahl der verkauften Autos. kann wie oben als binomialverteilt angenommen werden mit und 
. In Formeln lautet die Bedingung für unser
: {
}. Daraus folgt:
Betrachte nun die Tabelle zur kumulierten Binomialverteilung für
und .
Du findest den Wert für durch systematisches Probieren:
: zu groß
: okay
Damit ist 
, also 
. Mit einer Wahrscheinlichkeit von mehr als werden mindestens 34 Autos verkauft.
12.
a)
Wenn keine Qualitätsverbesserung eingetreten ist, beträgt die Wahrscheinlichkeit für einen nicht der Norm entsprechenden Pommes 
. Da die satte Prämie nur dann ausbezahlt wird, wenn oder weniger Pommes unter den 200 Pommes der Stichprobe sind, muss Folgendes gelten:
sei die Zufallsvariable, die die Anzahl der nicht der Norm entsprechenden Pommes beschreibt. ist dann 
(binomial)-verteilt.
Damit beträgt die Wahrscheinlichkeit, dass zufällig weniger als 18 Pommes aussortiert werden müssen 
. Mit dieser Wahrscheinlichkeit würde das Expertenteam eine Prämie erhalten, ohne eine Qualitätsverbesserung bewirkt zu haben.
b)
Ist die Wahrscheinlichkeit auf gesunken, so ergibt sich eine neue (binomial)-Verteilung.
Sei wie in a), dann ist 
(binomial)-verteilt.
Da die für die Prämie immer noch die Voraussetzung von oder weniger fehlerhaften Pommes gilt, erhält man
Somit besteht eine Wahrscheinlichkeit von 
, dass unter den 200 Pommes mehr als 18 Stück sind, die aussortiert werden müssen, obwohl der Ausschuss durch die Qualitätsverbesserung unter gesenkt wurde.
13.
Sei die Zufallsvariable, die die Anzahl der Personen in der Stichprobe von beschreibt, die das Angebot des IT-Fachmarktes kennen.
Dann ist 
-(binomial)verteilt. Wenn die Wahrscheinlichkeit mehr als betragen soll, muss man ein finden, so dass gilt:
Schaut man sich nun die Tabelle der aufsummierten Binomialverteilung (kumulative Verteilungsfunktion) an, so findet man nur die Wahrscheinlichkeiten unterhalb von 0,5, also 
. Wir brauchen also das Gegenereignis:
Den Wert für 
kann man nun aus der Tabelle für die kumulative Verteilungsfunktion ablesen.
ist also zu groß
Die Lösung mit 
ist somit diejenige, welche die Bedingung erfüllt. Für das gesuchte gilt also 
. Also mindestens 187 Befragte sollten die Werbung kennen.
Dann ist