Gerade - Ebene

Es gibt drei Möglichkeiten, wie eine Gerade und eine Ebene zueinander liegen können:

Art der Lage	Anzahl gemeinsamer Punkte	...
Gerade liegt in der Ebene	$\infty$	...
sie schneiden sich	$1$	...
parallel	$0$	...

Vollständige Tabelle anzeigen

Art der Lage	Anzahl gemeinsamer Punkte	Parallelität	Skizze
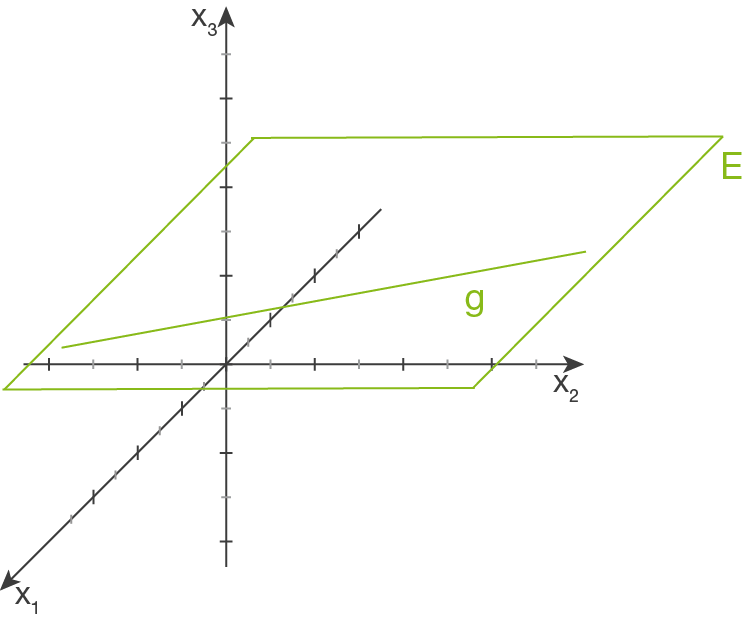
Gerade liegt in der Ebene	$\infty$
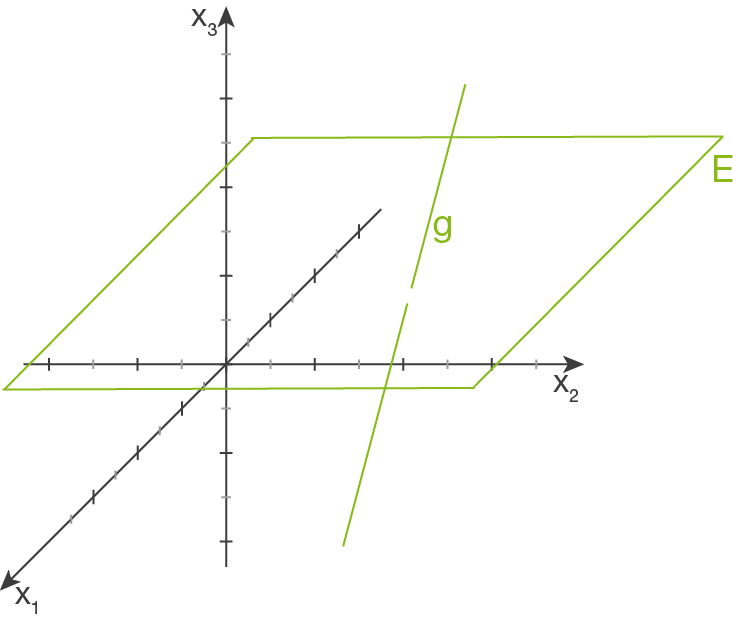
sie schneiden sich	$1$
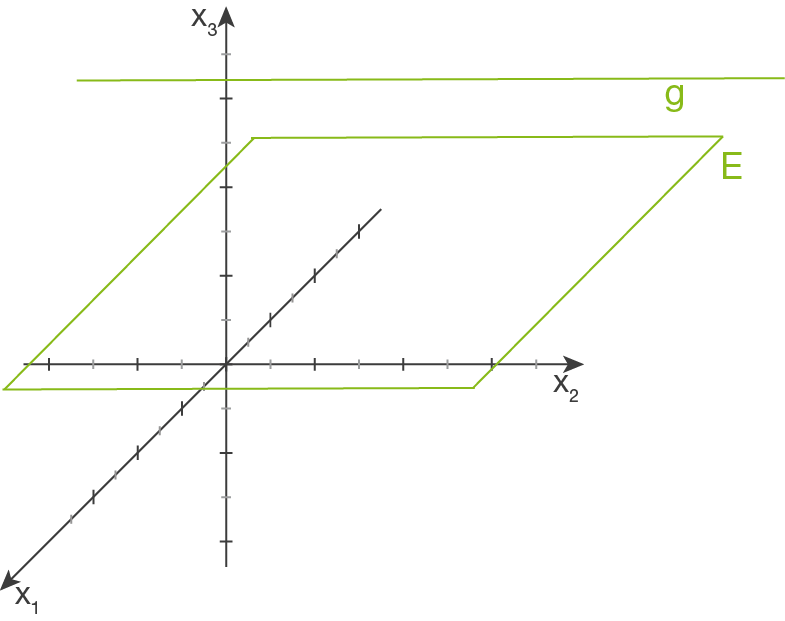
parallel	$0$

Vorgehen

Um die gegenseitige Lage zu bestimmen, gehe wie bei der Berechnung des Schnittpunkts vor. Je nachdem in welcher Form die Ebenengleichung gegeben ist, folge dazu folgenden Schritten:

Parameterform: Gleichsetzen
Koordinaten-/Normalenform: Einsetzen der Koordinaten des allgemeinen Geradenpunkts in die Ebenengleichung

Lösen des dadurch entstehenden linearen Gleichungssystems bzw. der Gleichung:
Das LGS/Die Gleichung hat
- unendlich viele Lösungen $\Rightarrow$ Die Gerade liegt in der Ebene.
- keine Lösung $\Rightarrow$ Die Gerade verläuft parallel zur Ebene.
- eine Lösung $\Rightarrow$ Die Gerade schneidet die Ebene.

Gibt es einen Schnittpunkt, so kannst du die Koordinaten bestimmen, indem du den berechneten Parameterwert für die Gerade in die Geradengleichung einsetzt.

Untersuche die Lage der Geraden zur Ebene (Ebene in Parameterform).

$g:\;\overrightarrow{x} = \left( {\begin{array}{c} 6 \\ -1 \\ 10 \\ \end{array}} \right)+ t\left( {\begin{array}{c} 1 \\ -1 \\ 3 \\ \end{array}} \right)$ ,

$E:\;\overrightarrow{x} = \left( {\begin{array}{c} 1 \\ -2 \\ 4 \\ \end{array}} \right) + r\left( {\begin{array}{c} 1 \\ 3 \\ 5 \\ \end{array}} \right) + s\left( {\begin{array}{c} 2 \\ 0 \\ 1 \\ \end{array}} \right)$ .

$g:\;\overrightarrow{x} = \left( {\begin{array}{c} 5 \\ 7 \\ 9 \\ \end{array}} \right)+ t\left( {\begin{array}{c} 8 \\ 6 \\ 3 \\ \end{array}} \right)$ ,

$E:\;\overrightarrow{x} = \left( {\begin{array}{c} 3 \\ 4 \\ 6 \\ \end{array}} \right) + r\left( {\begin{array}{c} 5 \\ 3 \\ 9 \\ \end{array}} \right) + s\left( {\begin{array}{c} 4 \\ 2 \\ 1 \\ \end{array}} \right)$ .

$g:\;\overrightarrow{x} = \left( {\begin{array}{c} 4 \\ 7 \\ 8 \\ \end{array}} \right)+ t\left( {\begin{array}{c} 8 \\ 6 \\ 3 \\ \end{array}} \right)$ ,

$E:\;\overrightarrow{x} = \left( {\begin{array}{c} 2 \\ 8 \\ 5 \\ \end{array}} \right) + r\left( {\begin{array}{c} 16 \\ 12 \\ -6 \\ \end{array}} \right) + s\left( {\begin{array}{c} 4 \\ 3 \\ 1 \\ \end{array}} \right)$ .

$g:\;\overrightarrow{x} = \left( {\begin{array}{c} 8 \\ 12 \\ 9 \\ \end{array}} \right)+ t\left( {\begin{array}{c} -9 \\ 6 \\ 3 \\ \end{array}} \right)$ ,

$E:\;\overrightarrow{x} = \left( {\begin{array}{c} 3 \\ 8 \\ 7 \\ \end{array}} \right) + r\left( {\begin{array}{c} 5 \\ 4 \\ 2 \\ \end{array}} \right) + s\left( {\begin{array}{c} 3 \\ 2 \\ 1 \\ \end{array}} \right)$ .

Untersuchen Sie die Lage der Geraden zur Ebene (Ebene in Koordinatenform).

$g:\;\overrightarrow{x} = \left( {\begin{array}{c} 2 \\ -5 \\ 2 \\ \end{array}} \right)+ t\left( {\begin{array}{c} 2 \\ -4 \\ 1 \\ \end{array}} \right)$ ,

$E:\;2x_1+x_2=-1$ .

$g:\;\overrightarrow{x} = \left( {\begin{array}{c} 3 \\ 5 \\ 1 \\ \end{array}} \right)+ t\left( {\begin{array}{c} 3 \\ -4 \\ 5 \\ \end{array}} \right)$ ,

$E:\;x_1+2x_2+x_3=-6$ .

$g:\;\overrightarrow{x} = \left( {\begin{array}{c} 3 \\ 4 \\ 2 \\ \end{array}} \right)+ t\left( {\begin{array}{c} 5 \\ -6 \\ 9 \\ \end{array}} \right)$ ,

$E:\;2x_1+3x_2+x_3=8$ .

$g:\;\overrightarrow{x} = \left( {\begin{array}{c} 4 \\ -8 \\ 3 \\ \end{array}} \right)+ t\left( {\begin{array}{c} 3 \\ 4 \\ 6 \\ \end{array}} \right)$ ,

$E:\;x_1+2x_2+x_3=-6$ .

Bestimme den Parameter $t$ so, dass die Gerade und die Ebene parallel zueinander sind.

$g:\overrightarrow{x}=\left(\begin{array}{r} -2\\ 3\\ 1\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 1\\ t\\ -2\\ \end{array}\right)$ , $\qquad$ $E:2x_1+x_2+2x_3=4$ .

$g:\overrightarrow{x}=\left(\begin{array}{r} 0\\ 2\\ -4\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 2\\ 1\\ 4\\ \end{array}\right)$ , $\qquad$ $E:tx_1+2x_2-x_3=2$ .

$g:\overrightarrow{x}=\left(\begin{array}{r} 4\\ -1\\ 1\\ \end{array}\right)+u\cdot\left(\begin{array}{r} 1\\ 1\\ t\\ \end{array}\right)$ $\qquad$

Gerade - Ebene

Vorgehen

Weiter lernen mit SchulLV-PLUS!

Weiter lernen mit SchulLV-PLUS!