Funktionen mit Parametern
Einführung
Wenn du eine Funktion mit einem Parameter gegeben hast, kannst du die Kurvendiskussion so durchführen, wie wenn du die Funktion ohne Parameter gegeben hättest. Du kannst die Funktion auf folgenden Eigenschaften untersuchen:- Definitionsbereich
- Nullstellen
- Schnittpunkte mit der
-Achse
- Grenzwerte
- Extrema
- Wendepunkte
- Symmetrie
Beispiel
1.
Funktionsuntersuchung mit Parametern
Sei mit
mit  eine Funktionenschar,
eine Funktionenschar,  . Treffe Aussagen über
. Treffe Aussagen über
Sei
a)
den Definitionsbereich von 
b)
die Symmetrie der Schaubilder von 
c)
Schnittpunkte mit den Achsen der Schaubilder von 
d)
Extremstellen von 
2.
Schaubilder von Funktionen mit Parametern
Gegeben sind die folgenden Funktionsscharen.
Beschreibe die Veränderung des Schaubildes bei einer Änderung von .
.
Haben die Schaubilder gemeinsame Punkte? (Tipp: Skizziere dir einige Schaubilder für unterschiedliche Werte von )
)
Für welches geht das Schaubild von
geht das Schaubild von  durch die Punkte
durch die Punkte  und
und  ?
?

 und
und 

 und
und 

 und
und 

 und
und 
Beschreibe die Veränderung des Schaubildes bei einer Änderung von
Haben die Schaubilder gemeinsame Punkte? (Tipp: Skizziere dir einige Schaubilder für unterschiedliche Werte von
Für welches
a)
b)
c)
d)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
Funktionsuntersuchung mit Parametern
 ist eine ganzrationale Funktion und besitzt als solche keine Definitionslücken. Damit gilt für den Definitionsbereich:
ist eine ganzrationale Funktion und besitzt als solche keine Definitionslücken. Damit gilt für den Definitionsbereich:  .
.
 Schnittpunkte mit der
Schnittpunkte mit der  -Achse
Setze
-Achse
Setze  :
:
 Betrachte die Diskriminante
Betrachte die Diskriminante  .
.
Aus diesem Ausdruck kann nur die Wurzel gezogen werden, wenn ist, andernfalls nicht. Damit folgt:
Für
ist, andernfalls nicht. Damit folgt:
Für  besitzen die Schaubilder von
besitzen die Schaubilder von  keinen Schnittpunkt mit der
keinen Schnittpunkt mit der  -Achse.
Für
-Achse.
Für  schneiden die Schaubilder von
schneiden die Schaubilder von  die
die  -Achse in Punkten
-Achse in Punkten  und
und  .
.
 Schnittpunkt mit der
Schnittpunkt mit der  -Achse
Berechne
-Achse
Berechne  :
:
 . Damit folgt der Schnittpunkt mit der
. Damit folgt der Schnittpunkt mit der  -Achse:
-Achse:  .
.
a)
b)
Die Schaubilder von  sind achsensymmetrisch zur
sind achsensymmetrisch zur  -Achse, da
-Achse, da 
ist. Dies gilt unabhängig von , also die Schaubilder aller Funktionen der Schar.
, also die Schaubilder aller Funktionen der Schar.
ist. Dies gilt unabhängig von
c)
Aus diesem Ausdruck kann nur die Wurzel gezogen werden, wenn
d)
Schritt 1: Ableitungen bestimmen
 Schritt 2: Notwendiges Kriterium für Extremstellen
Das notwendige Kriterium lautet:
Schritt 2: Notwendiges Kriterium für Extremstellen
Das notwendige Kriterium lautet: 
 Schritt 3: Hinreichendes Kriterium
Mit dem hinreichende Kriterium kannst du überprüfen, ob tatsächlich eine Extremstelle vorliegt. Außerdem kannst du die Art der Extremstelle bestimmen.
Schritt 3: Hinreichendes Kriterium
Mit dem hinreichende Kriterium kannst du überprüfen, ob tatsächlich eine Extremstelle vorliegt. Außerdem kannst du die Art der Extremstelle bestimmen.
 .
Hier ist eine Fallunterscheidung zu treffen:
.
Hier ist eine Fallunterscheidung zu treffen:
- Ist
, so ist
und damit liegt ein Minimum vor.
- Ist
, so ist
und damit liegt ein Maximum vor.
2.
Schaubilder von Funktionen mit Parametern

 Einfluss des Parameters beschreiben
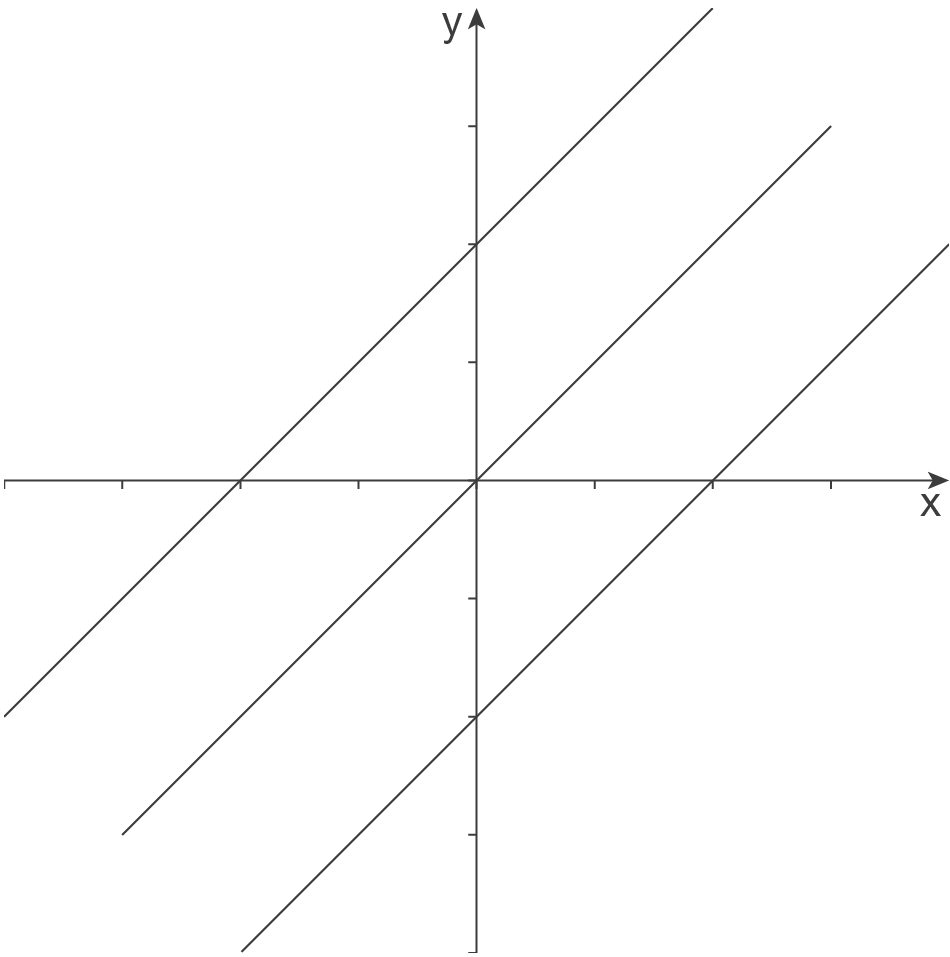
Die Schaubilder dieser Funktionenschar sind parallele Geraden mit der Steigung
Einfluss des Parameters beschreiben
Die Schaubilder dieser Funktionenschar sind parallele Geraden mit der Steigung  . Durch Variation von
. Durch Variation von  wird das Schaubild entlang der
wird das Schaubild entlang der  -Achse verschoben.
-Achse verschoben.
Aufgrund dieser Parallelität haben die Schaubilder keine gemeinsamen Punkte.
Die Abbildung unten zeigt die Schaubilder von für
für  .
.
 Wert für
Wert für  bestimmen
Das entsprechende
bestimmen
Das entsprechende  für die Punkte erhält man durch Einsetzen der Koordinaten Punkte in die Funktionsgleichung von
für die Punkte erhält man durch Einsetzen der Koordinaten Punkte in die Funktionsgleichung von  .
.



 Das Schaubild von
Das Schaubild von  verläuft durch
verläuft durch  , das von
, das von  durch
durch  .
.

 Einfluss des Parameters beschreiben
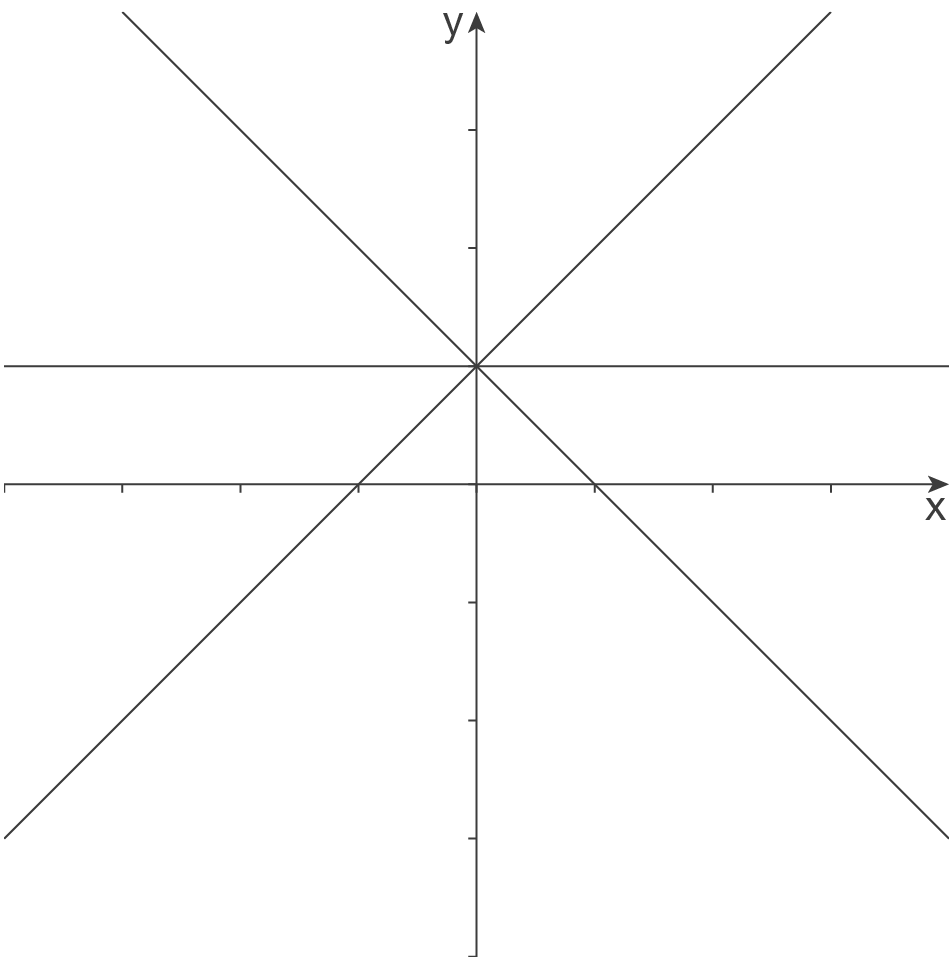
Die Schaubilder dieser Funktionenschar sind Geraden mit der Steigung
Einfluss des Parameters beschreiben
Die Schaubilder dieser Funktionenschar sind Geraden mit der Steigung  . Durch Variation von
. Durch Variation von  wird das Schaubild von
wird das Schaubild von  steiler oder flacher.
steiler oder flacher.
Die Abbildung unten zeigt die Schaubilder von für
für  .
.
 Gemeinsamen Punkt bestimmen
Wähle zwei beliebige Werte für
Gemeinsamen Punkt bestimmen
Wähle zwei beliebige Werte für  , z.B.
, z.B.  und
und  und berechne den Schnittpunkt der zugehörigen Schaubilder von
und berechne den Schnittpunkt der zugehörigen Schaubilder von  und
und  durch Gleichsetzen der Funktionsterme. Zeige anschließend durch eine Punktprobe, dass dieser Punkt auf allen Geraden der Schar liegt.
durch Gleichsetzen der Funktionsterme. Zeige anschließend durch eine Punktprobe, dass dieser Punkt auf allen Geraden der Schar liegt.
 Setze
Setze  ein in eine der beiden Funktionsgleichungen, z.B.:
ein in eine der beiden Funktionsgleichungen, z.B.:  . Damit folgt der Schnittpunkt
. Damit folgt der Schnittpunkt  .
Setze nun die Koordinaten von
.
Setze nun die Koordinaten von  in die Funktionsgleichung von
in die Funktionsgleichung von  ein und zeige so, dass
ein und zeige so, dass  auf allen Geraden der Schar liegt:
auf allen Geraden der Schar liegt:
 Damit ist gezeigt: Alle Geraden der Schar verlaufen durch den Punkt
Damit ist gezeigt: Alle Geraden der Schar verlaufen durch den Punkt  .
.
 Wert für
Wert für  bestimmen
bestimmen



 Das Schaubild von
Das Schaubild von  verläuft durch
verläuft durch  , das von
, das von  durch
durch  .
.

 Einfluss des Parameters beschreiben
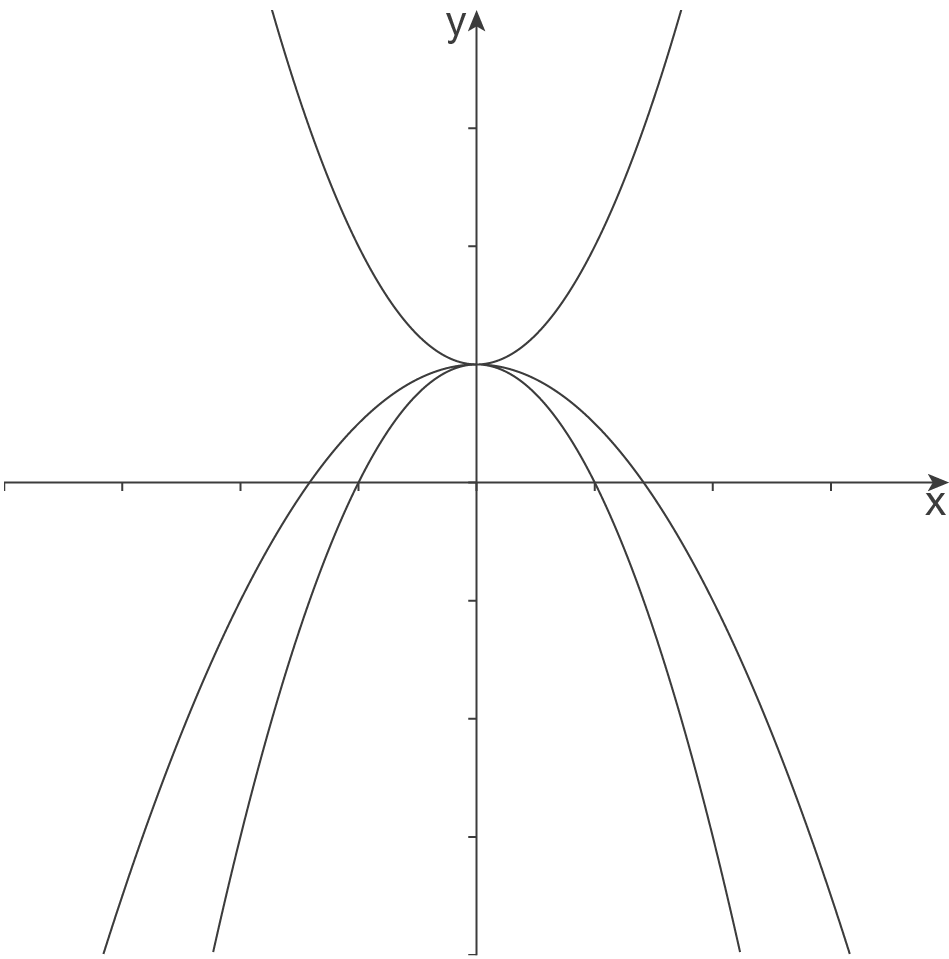
Die Schaubilder dieser Funktionenschar sind Parabeln mit dem
Einfluss des Parameters beschreiben
Die Schaubilder dieser Funktionenschar sind Parabeln mit dem  -Achsenabschnitt
-Achsenabschnitt  , d.h. sie alle schneiden die
, d.h. sie alle schneiden die  -Achse im Punkt
-Achse im Punkt  . Dies ist auch der gemeinsame Punkt (Rechnung siehe unten).
. Dies ist auch der gemeinsame Punkt (Rechnung siehe unten).
Je nach Wahl von ist das Schaubild von
ist das Schaubild von  entweder nach oben
entweder nach oben  oder nach unten
oder nach unten  geöffnet. Außerdem wird das Schaubild durch
geöffnet. Außerdem wird das Schaubild durch  gestaucht oder gestreckt. Die Abbildung unten zeigt die Schaubilder von
gestaucht oder gestreckt. Die Abbildung unten zeigt die Schaubilder von  für
für  .
.
 Gemeinsamen Punkt bestimmen
Wähle zwei beliebige Werte für
Gemeinsamen Punkt bestimmen
Wähle zwei beliebige Werte für  , z.B.
, z.B.  und
und  und berechne den Schnittpunkt der zugehörigen Schaubilder von
und berechne den Schnittpunkt der zugehörigen Schaubilder von  und
und  durch Gleichsetzen der Funktionsterme. Zeige anschließend durch eine Punktprobe dass dieser Punkt auf allen Geraden der Schar liegt.
durch Gleichsetzen der Funktionsterme. Zeige anschließend durch eine Punktprobe dass dieser Punkt auf allen Geraden der Schar liegt.
 Setze
Setze  ein in eine der beiden Funktionsgleichungen, z.B.:
ein in eine der beiden Funktionsgleichungen, z.B.:  . Damit folgt der Schnittpunkt
. Damit folgt der Schnittpunkt  .
Setze nun die Koordinaten von
.
Setze nun die Koordinaten von  in die Funktionsgleichung von
in die Funktionsgleichung von  ein und zeige so, dass
ein und zeige so, dass  auf allen Geraden der Schar liegt:
auf allen Geraden der Schar liegt:
 Damit ist gezeigt: Alle Geraden der Schar verlaufen durch den Punkt
Damit ist gezeigt: Alle Geraden der Schar verlaufen durch den Punkt  .
.
 Wert für
Wert für  bestimmen
bestimmen



 Das Schaubild von
Das Schaubild von  verläuft durch
verläuft durch  , das von
, das von  durch
durch  .
.

 Einfluss des Parameters beschreiben
Bei solchen Funktionen, bei denen der Parameter
Einfluss des Parameters beschreiben
Bei solchen Funktionen, bei denen der Parameter  mehrmals im Funktionsterm vorkommt kann es nützlich sein, die Funktion nicht als ganzes sondern in kleineren Teilen zu betrachten.
mehrmals im Funktionsterm vorkommt kann es nützlich sein, die Funktion nicht als ganzes sondern in kleineren Teilen zu betrachten.
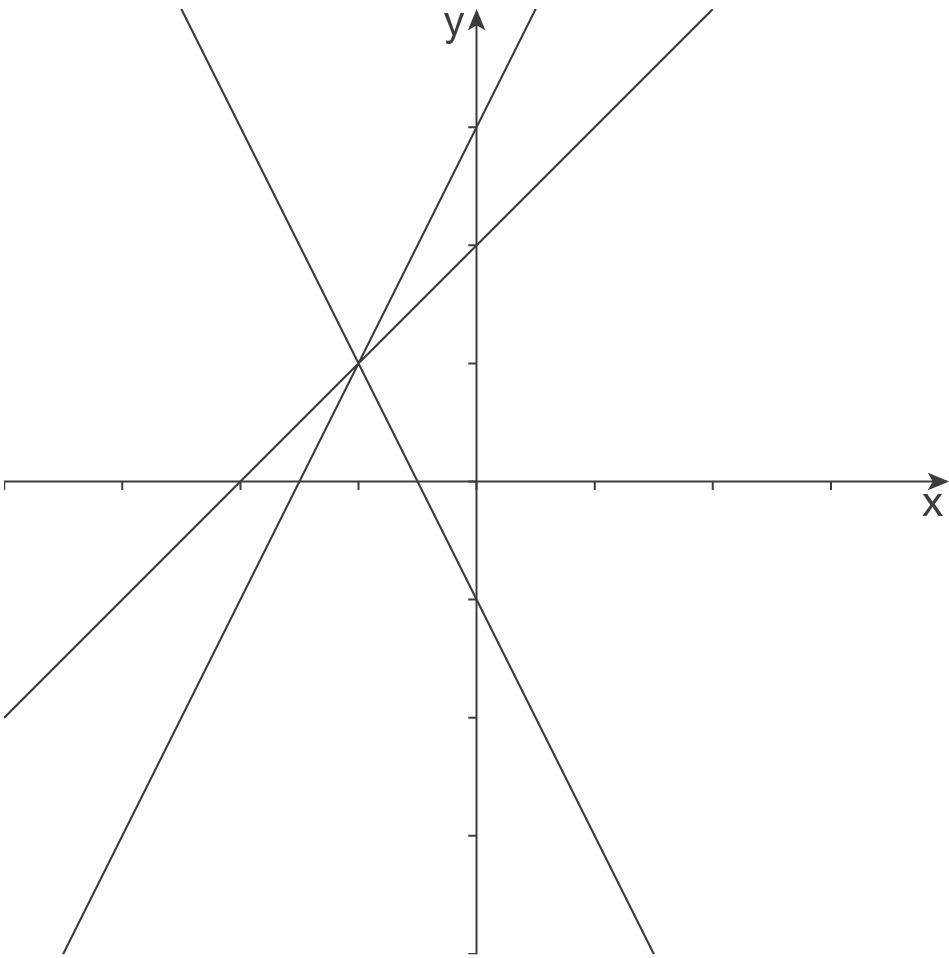
Die Schaubilder dieser Funktionenschar sind Geraden mit der Steigung . Der Schnittpunkt mit der
. Der Schnittpunkt mit der  -Achse kann durch Einsetzen von
-Achse kann durch Einsetzen von  bestimmt werden:
bestimmt werden:  .
.
Durch Variation von ändert sich also sowohl die Steigung als auch der
ändert sich also sowohl die Steigung als auch der  -Achsenabschnitt des Schaubildes von
-Achsenabschnitt des Schaubildes von  .
.
Die Abbildung unten zeigt die Schaubilder von für
für  .
.
 Gemeinsamen Punkt bestimmen
Wähle zwei beliebige Werte für
Gemeinsamen Punkt bestimmen
Wähle zwei beliebige Werte für  , z.B.
, z.B.  und
und  und berechne den Schnittpunkt der zugehörigen Schaubilder von
und berechne den Schnittpunkt der zugehörigen Schaubilder von  und
und  durch Gleichsetzen der Funktionsterme. Zeige anschließend durch eine Punktprobe, dass dieser Punkt auf allen Geraden der Schar liegt.
durch Gleichsetzen der Funktionsterme. Zeige anschließend durch eine Punktprobe, dass dieser Punkt auf allen Geraden der Schar liegt.
 Setze
Setze  ein in eine der beiden Funktionsgleichungen, z.B.:
ein in eine der beiden Funktionsgleichungen, z.B.:  . Damit folgt der Schnittpunkt
. Damit folgt der Schnittpunkt  .
Setze nun die Koordinaten von
.
Setze nun die Koordinaten von  in die Funktionsgleichung von
in die Funktionsgleichung von  ein und zeige so, dass
ein und zeige so, dass  auf allen Geraden der Schar liegt:
Damit ist gezeigt: Alle Geraden der Schar verlaufen durch den Punkt
auf allen Geraden der Schar liegt:
Damit ist gezeigt: Alle Geraden der Schar verlaufen durch den Punkt  .
.
 Wert für
Wert für  bestimmen
bestimmen



 Das Schaubild von
Das Schaubild von  verläuft durch
verläuft durch  , das von
, das von  durch
durch  .
.
a)
Aufgrund dieser Parallelität haben die Schaubilder keine gemeinsamen Punkte.
Die Abbildung unten zeigt die Schaubilder von

b)
Die Abbildung unten zeigt die Schaubilder von

c)
Je nach Wahl von

d)
Die Schaubilder dieser Funktionenschar sind Geraden mit der Steigung
Durch Variation von
Die Abbildung unten zeigt die Schaubilder von
