Angewandte Integrale

Oft hast du anwendungsbezogene Aufgabenstellungen vor dir. Dabei kommt es darauf an, die Formulierungen richtig zu interpretieren. Ist dir eine Funktion $f$ gegeben, wobei $f(x)$ eine Zuflussrate, Wachstumsrate, Geschwindigkeit oder ähnliches angibt, ist $f(x)$ also zum Beispiel die Wassermenge die pro Stunde in ein Becken fließt, so beschreibt $f$ eine Änderungsrate. Mit einem Integral kannst du dann im Fall der Wassermenge beispielsweise, berechnen wie viel Wasser in einem bestimmten Zeitintervall in das Becken geflossen ist. Beschreibt $f$ die Geschwindigkeit eines Autos, Fahrrads oder Ähnlichem, dann kannst du mit einem Integral die zurückgelegte Strecke im jeweiligen Intervall berechnen. Die Wassermenge oder zurückgelegte Strecke nach $x$ Zeiteinheiten ergibt sich dann durch den Funktionswert einer geeigneten Stammfunktion, wobei die Konstante $c$ die Wassermenge beschreibt, die zu Beginn der Beobachtung bereits im Becken war. Diese Zusammenhänge lassen sich auf viele weitere Sachverhalte übertragen.
Achte also auf Worte wie „Rate“, „Geschwindigkeit“ oder „pro Minute/Stunde/...“.

Der Zu- und Abfluss eines Wassersilos kann durch die Funktion $f$ mit $f(t)=-2t+8$ beschrieben werden.
Dabei steht $t$ für Stunden und $f(t)$ für den Zu- bzw. Abfluss in Liter pro Stunde.
Zu Beginn ist das Wassersilo mit 1000 Litern gefüllt.

Wieviel Wasser enthält das Wassersilo

nach 10 Stunden?

Ein Mobilfunkdienstleister wirbt damit, dass der Preis pro Minute für ein Telefonat mit der Anzahl der Minuten sinkt. Das Tarifsystem wird beschrieben durch die Funktion $f$ mit

$f(x)=\dfrac{10}{(x+1)^2}+0,05$

mit $x\geq0$ , wobei $x$ die Anzahl

der Minuten und $f(x)$ den Minutentarif

der $x$ -ten Minute in Euro beschreibt.

Berechne die Kosten der

Telefonrechnung nach 100 Gesprächsminuten. Was sind die durchschnittlichen Kosten pro Minute bei 100 Gesprächsminuten?

Die momentane Eintrittsrate der Besucher eines Pop-Konzertes - also die Eintrittsrate der Personen pro 10 Minuten - wird beschrieben durch die Funktion $f$ mit

$f(t)=1000-0,01\mathrm{e}^{t}; \; t\geq0$ ,

wobei $t$ die Zeit pro 10 Minuten und $f(t)$

die Anzahl der eintretenden Personen pro 10 Minuten beschreibt.

Wann kommen keine Personen mehr in

den Konzertraum? Wie viele Personen

sind nach 70 Minuten bereits im Konzertraum? Wie viele Personen sind in diesen 70 Minuten im Schnitt pro 10 Minuten in den Konzertraum gekommen?

Angaben zur Rechnung: $\ln100\,000\approx11,51$ und $\mathrm{e}^{7}\approx1097$ .

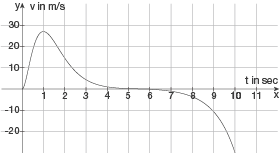
Das Schaubild unten beschreibt die Geschwindigkeit $v$ eines Balles, der von einer Kanone senkrecht nach oben geschossen wurde. (Der Ball wird zum Zeitpunkt $t=0$ abgeschossen. Die Abwärtsbewegung des Balles entspricht einer negativen Geschwindigkeit. $t$ in Sekunden, $v$ in Meter pro Sekunde.)

Nach wie vielen Sekunden ist der Ball an seinem höchsten Punkt angelangt?

Schätze anhand des Schaubilds, wie hoch der Ball geflogen ist. Wie viele Meter ist der Ball nach 10 Sekunden vom Boden entfernt?

Graph zeigt die Geschwindigkeit v in m/s über die Zeit t in Sekunden.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Die Funktion $f$ beschreibt die Abflussrate des Wassers zum Zeitpunkt $t$ . Die tatsächliche Menge an Wasser, die zum Zeitpunkt $t$ noch im Silo vorhanden ist, wird durch eine

Stammfunktion beschrieben.

Allgemein hat diese Stammfunktion die Gleichung $F(t)=-t^2+8t+c$ .

In der Aufgabenstellung ist

angegeben, dass das Wassersilo zu

Beginn ( $t=0$ ) mit 1000 Litern

gefüllt war. Daraus ergibt sich das Wertepaar $(0;1000)$ bzw. die Bedingung $F(0)=1000$ .

Setze ein in $F(t)$ und berechne $c$ :

$\begin{array}[t]{rrl} F(0)=&1.000=&-0^2+8\cdot0+c\\ &1.000=&c \end{array}$

Also ist $F(t)=-t^2+8t+1000$ .

Gefragt ist nach der Wassermenge,

die nach 10 Stunden

im Silo vorhanden ist. Sie entspricht dem Wert $F(10)$ :

$F(10)=-10^2+8\cdot10+1000=980$

Das Wassersilo enthält nach 10 Stunden noch 980 Liter Wasser.

Die Funktion $f$ gibt dir den momentanen Minutentarif an, also den Tarif, den du in der $x$ -ten Minute bezahlen musst. Deshalb gibt dir eine Stammfunktion $F$ die Summe an, die bis zur $x$ -ten Minute insgesamt bezahlt werden muss.

Gefragt ist nach den gesamten Telefonkosten nach 100 Minuten. Integriere f also von $x=0$ bis $x=100$ :

$\begin{array}[t]{rlll} \displaystyle\int_{0}^{100}\left(\dfrac{10}{(x+1)^2}+0,05\right)\;\mathrm dx \end{array}$

Vollständige Lösung anzeigen

Die Telefonkosten für die ersten 100 Minuten sind damit $\approx14,90$ Euro.

Nun zu den durchschnittlichen Kosten:

Teile die Gesamtkosten durch die Anzahl der Minuten:

$\dfrac{14,90}{100}=0,149$ Euro pro Minute.

Die Funktion $f$ gibt an, wie viele Personen pro 10 Minuten ankommen. Die Anzahl der Personen, die nach einer bestimmten Zeit insgesamt im Konzertraum sind, wird also beschrieben durch eine Stammfunktion $F$ .

Zunächst ist danach gefragt, wann keine Personen mehr zum Konzert kommen, d.h.: Wann ist die Eintrittsrate Null? Setze $f(t)=0$ .

$\begin{array}[t]{rlll} f(t)=0&=1000-0,01\mathrm{e}^{t}\\[3pt] -1000&=-0,01\mathrm{e}^{t}\\[3pt] 100\,000&=\mathrm{e}^{t}\\[3pt] \ln100\,000&=t\approx11,51 \end{array}$

Nach $11,51\cdot10$ Minuten kommen keine Besucher mehr in den Konzertraum. Nach $115,1$ Minuten sind somit alle Zuschauer bei dem Pop-Konzert.

Die Anzahl der Personen, die nach 70 Minuten insgesamt im Konzertraum sind, kannst du nun durch Integration berechnen. Auf der $t$ -Achse wird die Zeit in 10-Minuten-Intervallen abgetragen. 70 Minuten entsprechen demnach dem Zeitpunkt $t=7$ .

Berechne also das Integral von

$f$ von $t=0$ bis $t=7$ :

$\begin{array}[t]{rlll} \displaystyle\int_{0}^{7}f(t)\;\mathrm dt&= \end{array}$

Vollständige Lösung anzeigen

Somit sind nach 70 Minuten schon 6989 Personen im Konzertraum.

Den Durchschnittswert erhältst du

wieder, indem du die Anzahl aller

Personen durch die Anzahl der vergangenen Minuten teilst. Achte darauf, dass als Zeiteinheit wieder ein 10-Minuten-Zeitraum gefordert ist.

$6989:7\approx998$ Personen pro

$10$ Minuten.

Die Funktion beschreibt die Geschwindigkeit des Balls. Dabei wird die Abwärtsbewegung des Balls durch eine negative Geschwindigkeit beschrieben.

Wichtig ist also: So lange der Graph

der Funktion oberhalb der $x$ -Achse verläuft, steigt der Ball. Wenn der Graph der Funktion unterhalb der $x$ -Achse verläuft, fällt der Ball.

Der Ball ist an seinem höchsten Punkt angelangt, wenn er aufhört zu steigen. Dies ist bei der Nullstelle der Funktion der Fall, also etwa bei $t=5$ .

Der Ball ist nach 5 Sekunden an

seinem höchsten Punkt angelangt.

Die Funktion $f$ gibt dir die Geschwindigkeit an. Also gibt dir das Integral von $f$ die zurückgelegte Strecke des Balls an.

Da der Ball nach 5 Sekunden an

seinem höchsten Punkt angelangt ist, kannst du seine maximale Höhe über das Integral $\displaystyle\int\limits_{0}^{5}f(t)\,\mathrm dt$ berechnen.

Anschaulich gibt dir das Integral den Inhalt A der Fläche an, die vom Graphen von $f$ und der $x$ -Achse zwischen $t=0$ und $t=5$ eingeschlossen wird.

Du kannst diese Fläche

näherungsweise durch zwei Dreiecke beschreiben. Für das Integral ergibt sich somit ein Näherungswert.

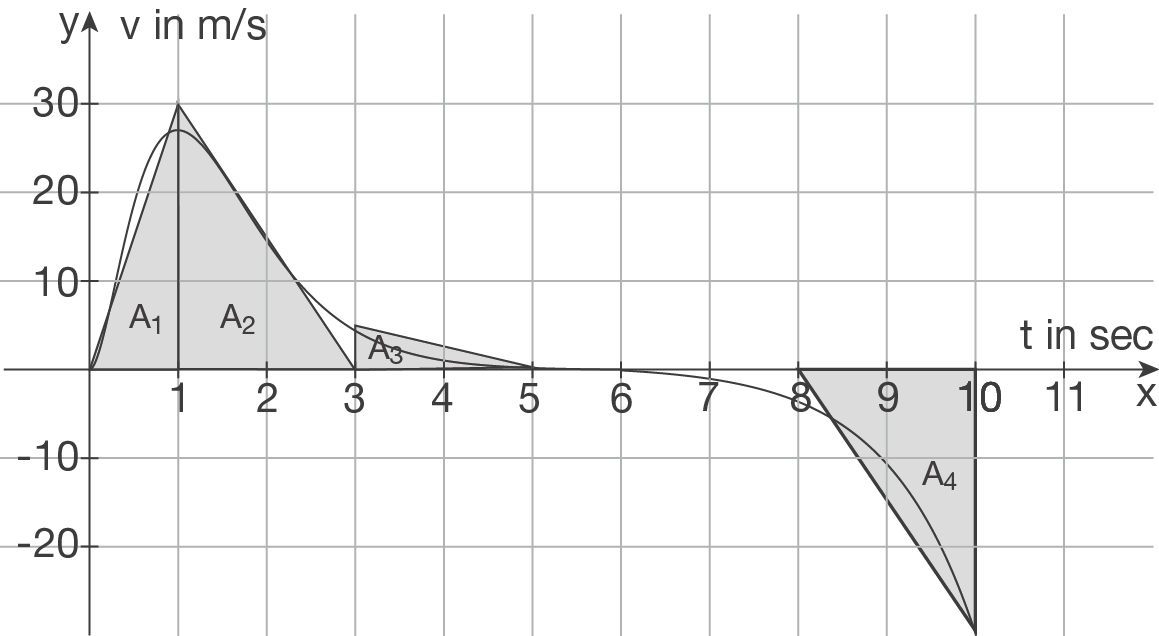Grafik zeigt eine Geschwindigkeitskurve über Zeit mit mehreren Flächen unter der Kurve.

Die Flächenstücke $A_1$ , $A_2$ und $A_3$

liegen oberhalb der $x$ -Achse und beschreiben somit gemeinsam die maximale Höhe des Balls:

$A_1=1\cdot3\cdot\dfrac{1}{2}=1,5$ ; $A_2=2\cdot3\cdot\dfrac{1}{2}=3$ ; $A_3=2\cdot0,5\cdot\dfrac{1}{2}=0,5$

Für $h=\displaystyle\int_{0}^{5} f(t) \;\mathrm dt$ ergibt sich somit näherungsweise $h=A_1+A_2+A_3=5$

Der Ball ist somit $50$ Meter hoch geflogen.

Das Dreieck $A_4$ liefert einen Näherungswert dafür, wie weit der Ball bis zur 10. Sekunde wieder gefallen ist:

$A_4=2\cdot3\cdot\dfrac{1}{2}=3$ /

Der Ball ist also $30$ Meter gefallen.

Somit ist der Ball nach $10$ Sekunden noch $20$ Meter vom Boden entfernt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?