Exponentialfunktionen
Exponentialfunktionen sind veränderte  -Funktionen:
-Funktionen:
 =
= Um eine solche Funktionsgleichung aufzustellen, musst du also
Um eine solche Funktionsgleichung aufzustellen, musst du also  ,
, ,
,  und
und  bestimmen.
Dazu benötigst du entsprechend der Anzahl der Unbekannten vier Bedingungen. Mögliche Bedingungen sind beispielsweise:
bestimmen.
Dazu benötigst du entsprechend der Anzahl der Unbekannten vier Bedingungen. Mögliche Bedingungen sind beispielsweise:
- Koordinaten von Punkten auf dem Graphen: Eingesetzt in die obige allgemeine Funktionsgleichung ergibt sich pro Punkt eine Gleichung
- Lage der waagerechten Asymptote: Die waagerechte Asymptote ist gleich dem Parameter
.
- Steigungswerte an bestimmten Stellen: Bilde die erste Ableitung der allgemeinen Funktion und setze dort ein.
1.
Die Funktionen haben die Form
 .
Gib jeweils einen möglichen Funktionsterm zur abgebildeten Funktion an.
.
Gib jeweils einen möglichen Funktionsterm zur abgebildeten Funktion an.
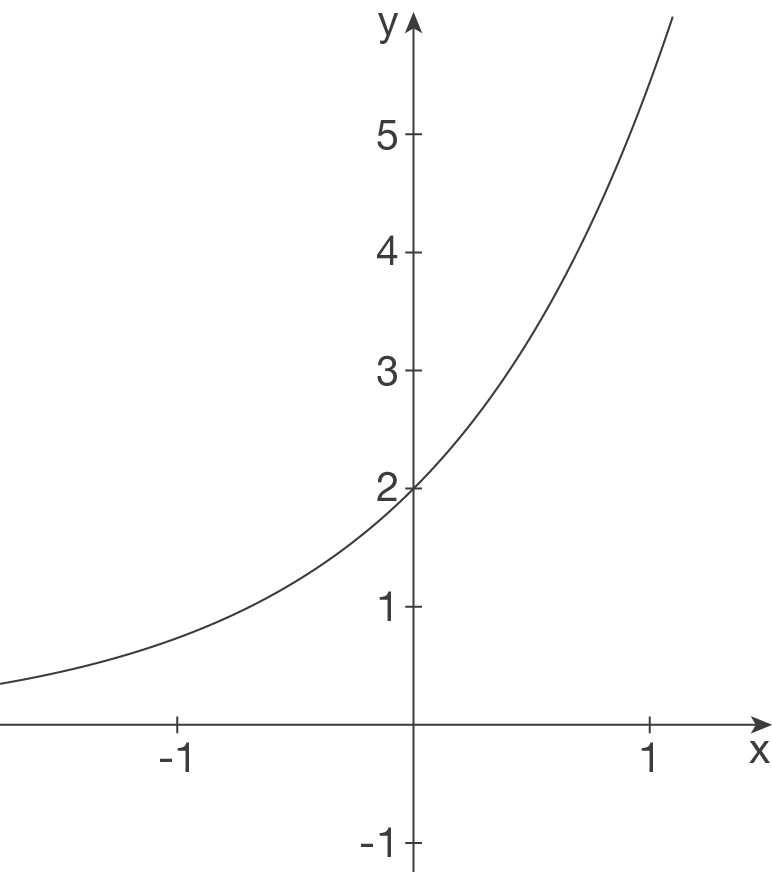
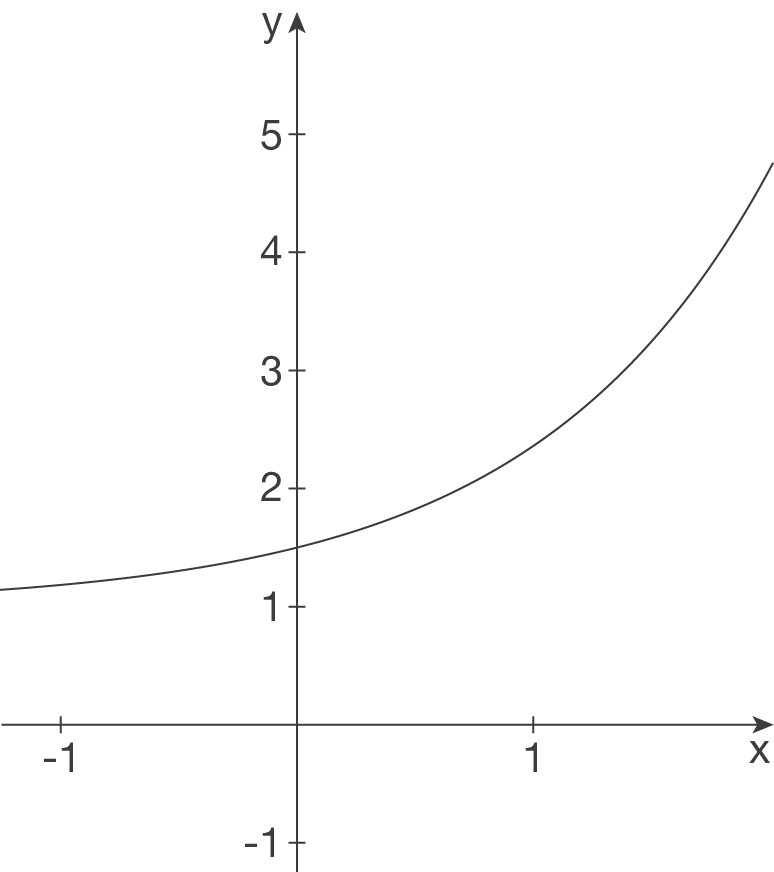
a)

- Waagrechte Asymptote bei
b)

- Waagrechte Asymptote bei
2.
Die allgemeine  -Funktion hat die Gestalt
-Funktion hat die Gestalt
 .
Sie beschreibt natürliches exponentielles Wachstum. Bestimme jeweils die Parameter
.
Sie beschreibt natürliches exponentielles Wachstum. Bestimme jeweils die Parameter  und
und  .
.
 Es ist
Es ist  und
und  .
.
 Es ist
Es ist  und
und  .
.
a)
b)
c)
Die gesuchte Funktion beschreibt das natürliche exponentielle Wachstum einer Bakterienkultur. Zu Beginn der Untersuchung geht man von 100 Bakterien in der Petri-Schale aus. Die Änderungsrate des Bakterienbestandes ist  .
.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
b)
2.
Der allgemeine Ansatz der  -Funktionen ist
-Funktionen ist
 .
Ihre Ableitung ist
.
Ihre Ableitung ist
 .
.
a)
Zunächst bestimmen wir  . Aus
. Aus  folgt
folgt 

 .
Setzt man nun
.
Setzt man nun  in die zweite Aussage über die Ableitung ein, so erhält man
in die zweite Aussage über die Ableitung ein, so erhält man  .
.
![\(\begin{array}[t]{rl@{\hspace{1cm}}l}
f‘(0)&=&3\\
k\cdot1\cdot\mathrm{e}^{k\cdot0}&=&3& \\
k&=&3& \\
\end{array}\)](https://mathjax.schullv.de/36d5f06ba496f3a1634f745219c1cb44f45f3acc5d01e1b8691be4a67034b08a?color=5a5a5a) Damit ist
Damit ist  .
.
b)
Zunächst bestimmen wir  . Aus
. Aus  folgt
folgt 

 .
Setzt man nun
.
Setzt man nun  in die zweite Aussage über die Ableitung ein, so erhält man
in die zweite Aussage über die Ableitung ein, so erhält man  .
.
![\(\begin{array}[t]{rl@{\hspace{1cm}}l}
f‘(0)&=8\\
k\cdot4\cdot\mathrm{e}^{k\cdot0}&=&8& \\
4k&=&8& \scriptsize\mid\;:4 \\
k&=&2& \\
\end{array}\)](https://mathjax.schullv.de/eca0f419eb0b41f7b4769a44f97c5e52362246cc7390c22c6c39c3a96149ebfb?color=5a5a5a) Damit ist
Damit ist  .
.
c)
Zunächst bestimmen wir wieder  . Wir wissen, dass der Anfangsbestand (
. Wir wissen, dass der Anfangsbestand ( ) 100 Bakterien sind. Demnach gilt
) 100 Bakterien sind. Demnach gilt  .
Es folgt
.
Es folgt 

 .
Setzt man nun
.
Setzt man nun  in die zweite Aussage über die Ableitung ein, so erhält man
in die zweite Aussage über die Ableitung ein, so erhält man  .
.
![\(\begin{array}[t]{rl@{\hspace{1cm}}l}
f‘(0)&=&2\\
k\cdot100\cdot\mathrm{e}^{k\cdot0}&=&2& \\
100k&=&2 &\scriptsize\mid\;:100 \\
k&=&0,02& \\
\end{array}\)](https://mathjax.schullv.de/825b7cc770f3a04e0e6eb12be54f235ab9bafdff62179fa462f361e2c566464e?color=5a5a5a) Damit ist
Damit ist  .
.