Spurgerade
Die Spurgeraden einer Ebene  sind die Schnittgeraden mit den Koordinatenebenen. Diese Schnittgeraden entsprechen den Verbindungsgeraden der Spurpunkte.
Für die Schnittgerade
sind die Schnittgeraden mit den Koordinatenebenen. Diese Schnittgeraden entsprechen den Verbindungsgeraden der Spurpunkte.
Für die Schnittgerade  mit der
mit der  -Ebene gilt
-Ebene gilt  .
Für die Schnittgerade
.
Für die Schnittgerade  mit der
mit der  -Ebene gilt
-Ebene gilt  .
Für die Schnittgerade
.
Für die Schnittgerade  mit der
mit der  -Ebene gilt
-Ebene gilt  .
.
 .
.
 Die Schnittgerade mit der
Die Schnittgerade mit der  -Ebene berechnest du, indem du
-Ebene berechnest du, indem du  in die Ebenengleichung einsetzt:
in die Ebenengleichung einsetzt:
 Setze
Setze  in die Gleichung ein und löse nach
in die Gleichung ein und löse nach  auf, dann kannst du die Geradengleichung in Parameterform aufstellen.
auf, dann kannst du die Geradengleichung in Parameterform aufstellen.
![\(\begin{array}[t]{rll}
4r + 2x_2&=&20 \quad \scriptsize \mid\; -4r\\[5pt]
2x_2&=&20-4r\quad \scriptsize \mid\; :2\\[5pt]
x_2&=&10-2r
\end{array}\)](https://mathjax.schullv.de/7a309dc1cdd590f90c8193459abbd91ca941ff0bebfd67dd4e4701e5b374d6b5?color=5a5a5a) Die Spurgerade für die
Die Spurgerade für die  -Ebene lautet:
-Ebene lautet:
 .
Die Schnittgerade mit der
.
Die Schnittgerade mit der  -Ebene berechnest du, indem du
-Ebene berechnest du, indem du  in die Ebenengleichung einsetzt:
in die Ebenengleichung einsetzt:
 Setze
Setze  in die Gleichung ein und löse nach
in die Gleichung ein und löse nach  auf, dann kannst du die Geradengleichung in Parameterform aufstellen.
auf, dann kannst du die Geradengleichung in Parameterform aufstellen.
![\(\begin{array}[t]{rll}
4s + 5x_3&=&20 \quad \scriptsize \mid\; -4s\\[5pt]
5x_3&=&20-4s\quad \scriptsize \mid\; :5\\[5pt]
x_3&=&4-\frac{4}{5}s
\end{array}\)](https://mathjax.schullv.de/e74f3fa9fc10ffdd551cb8ace6cbed35cddd57daf6776c55f07b9ab71f902ccf?color=5a5a5a) Die Spurgerade für die
Die Spurgerade für die  -Ebene lautet:
-Ebene lautet:
 .
Die Schnittgerade mit der
.
Die Schnittgerade mit der  -Ebene berechnest du, indem du
-Ebene berechnest du, indem du  in die Ebenengleichung einsetzt:
in die Ebenengleichung einsetzt:
 Setze
Setze  in die Gleichung ein und löse nach
in die Gleichung ein und löse nach  auf, dann kannst du die Geradengleichung in Parameterform aufstellen.
auf, dann kannst du die Geradengleichung in Parameterform aufstellen.
![\(\begin{array}[t]{rll}
2x_2 +5t&=&20 \quad \scriptsize \mid\; -5t\\[5pt]
2 x_2&=&20-5t\quad \scriptsize \mid\; :2\\[5pt]
x_2&=&10-2,5t
\end{array}\)](https://mathjax.schullv.de/754500fd13d5a18cc76b427f0743269286c9f3349955c9a6f197051dea98c008?color=5a5a5a) Die Spurgerade für die
Die Spurgerade für die  -Ebene lautet:
-Ebene lautet:
 .
.
 hat folgende Spurpunkte:
hat folgende Spurpunkte:
 ,
,  und
und  .
Bestimme die Spurgeraden der Ebene
.
Bestimme die Spurgeraden der Ebene  .
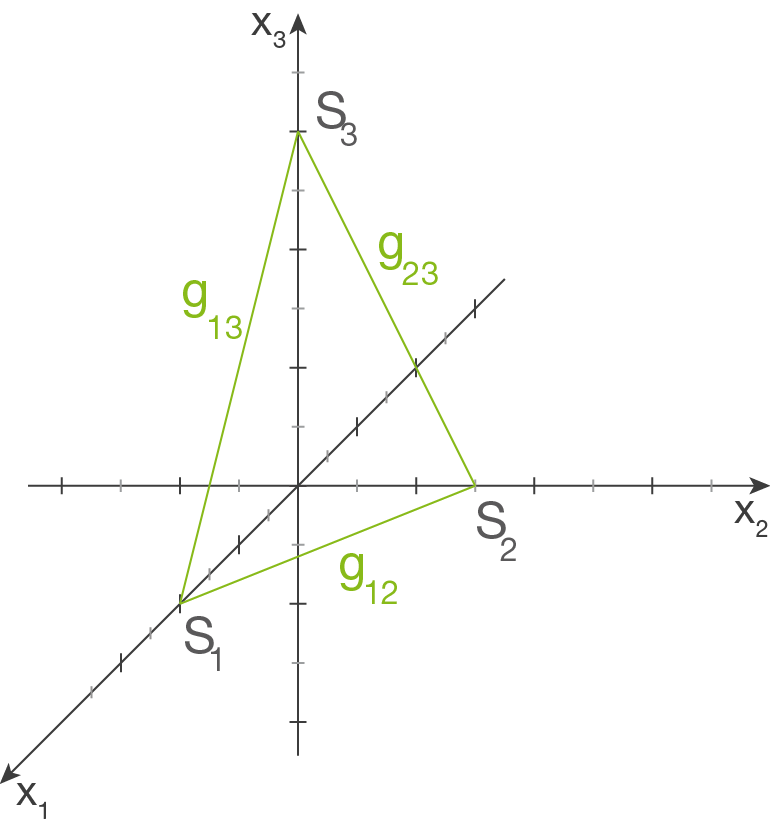
Die Spurgeraden sind gerade die Verbingungsgeraden der Spurpunkte.
Die Spurgerade für die
.
Die Spurgeraden sind gerade die Verbingungsgeraden der Spurpunkte.
Die Spurgerade für die  -Ebene lautet:
-Ebene lautet:
![\(\begin{array}[t]{rll}
g_{12}: \vec{x}&=& \overrightarrow{OS_1} + r\cdot \overrightarrow{S_1S_2} \\[5pt]
&=&\begin{pmatrix}-8\\0\\0\end{pmatrix} + r\cdot \begin{pmatrix}0-(-8)\\3-0\\0-0\end{pmatrix} \\[5pt]
&=&\begin{pmatrix}-8\\0\\0\end{pmatrix} + r\cdot \begin{pmatrix}8\\3\\0\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/57821cb6970b5f3a82c203a3144faa0a46edbd0f7cbafd6a45a17a1b67959d6b?color=5a5a5a) Die Spurgerade für die
Die Spurgerade für die  -Ebene lautet:
-Ebene lautet:
![\(\begin{array}[t]{rll}
g_{13}: \vec{x}&=& \overrightarrow{OS_1} + r\cdot \overrightarrow{S_1S_3} \\[5pt]
&=&\begin{pmatrix}-8\\0\\0\end{pmatrix} + r\cdot \begin{pmatrix}0-(-8)\\0-0\\5-0\end{pmatrix} \\[5pt]
&=&\begin{pmatrix}-8\\0\\0\end{pmatrix} + r\cdot \begin{pmatrix}8\\0\\5\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/04d899dca7e765b08e7521e5aa82d33bdb21d6e25ae40570351eeb98d2a88e06?color=5a5a5a) Die Spurgerade für die
Die Spurgerade für die  -Ebene lautet:
-Ebene lautet:
![\(\begin{array}[t]{rll}
g_{23}: \vec{x}&=& \overrightarrow{OS_2} + r\cdot \overrightarrow{S_2S_3} \\[5pt]
&=&\begin{pmatrix}0\\3\\0\end{pmatrix} + r\cdot \begin{pmatrix}0-0\\0-3\\5-0\end{pmatrix} \\[5pt]
&=&\begin{pmatrix}0\\3\\0\end{pmatrix} + r\cdot \begin{pmatrix}0\\-3\\5\end{pmatrix} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/2215ea4edb9838cd144f0acd5587cc094f017419d365fdbe8236c484eab2cd73?color=5a5a5a)
