Lerninhalte in Mathe

Mündliche Abi-Aufgaben

Digitales Schulbuch

Inhaltsverzeichnis

Vermischte Aufgaben

1.

Weisen Sie nach, dass die Schnittwinkel zwischen der Ebene $E:2x_2+x_3=4$ und der Ebene $F:-3x_1+x_2-x_3=9$ genauso groß ist wie der zwischen $E$ und der Ebene

$G:\overrightarrow{x}=\left(\begin{array}{r} 1\\ 1\\ 2\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 1\\ 1\\ 4\\ \end{array}\right)+s\cdot\left(\begin{array}{r} 1\\ 0\\ 3\\ \end{array}\right)$

2.

Gegeben ist eine Ebene $E:x_1-x_2+3x_3=4$ . Eine zweite Ebene $F$ wird aufgespannt von Geraden mit den Richtungsvektoren

$\overrightarrow{u}=\left(\begin{array}{r} 1\\ 1\\ 2\\ \end{array}\right)$ und $\overrightarrow{v}=\left(\begin{array}{r} -1\\ 0\\ 3\\ \end{array}\right)$ .

Berechnen Sie den Schnittwinkel von $E$ und $F$ .

3.

Gegeben sind die Punkte $A\left(1\mid 2\mid 1\right)$ , $B\left(2\mid 1\mid -2\right)$ , $C\left(3\mid 0\mid 4\right)$ und $D\left(4\mid 4\mid 2\right)$ .

Die Ebene $E$ wird aufgespannt von den Punkten $A$ , $B$ , $C$ , die Ebene $F$ von den Punkten $A$ , $B$ , $D$ .

Bestimmen Sie den Schnittwinkel der beiden Ebenen.

4.

Eine Gerade der Geradenschar

$g:\overrightarrow{x}=\left(\begin{array}{r} 1\\ 3\\ 2\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 1\\ k\\ 1\\ \end{array}\right)$

schneidet die Ebene $E:x_2+x_3=2$ unter einem Winkel von $60^{\circ}$ .

Welche ist das?

5.

Gegeben ist die Ebene $E:2x_1+2x_2-x_3=4$ . Berechnen Sie die Winkel zwischen der Ebene und den einzelnen Koordinatenachsen.

6.

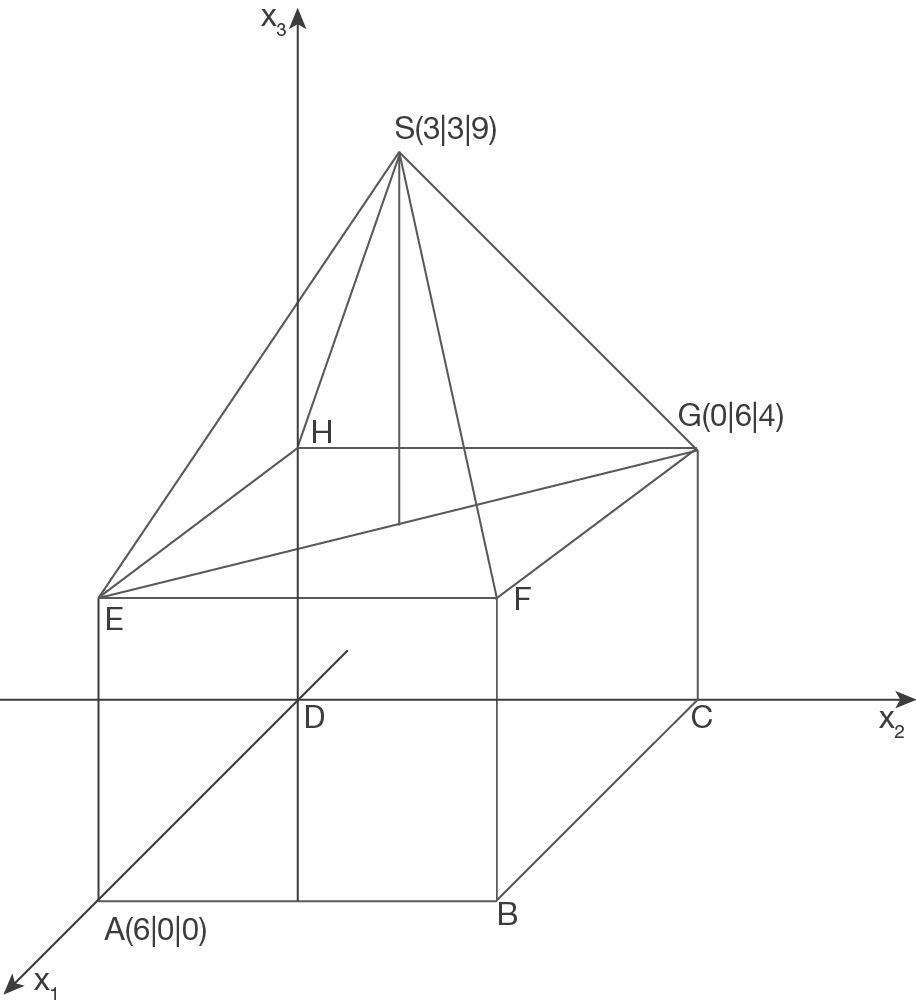
Berechnen Sie den Schnittwinkel der Dachkante $\overline{GS}$ mit der Diagonalen $\overline{EG}$ .

3D-Diagramm mit Punkten und Linien im Raum, dargestellt in einem Koordinatensystem.

7.

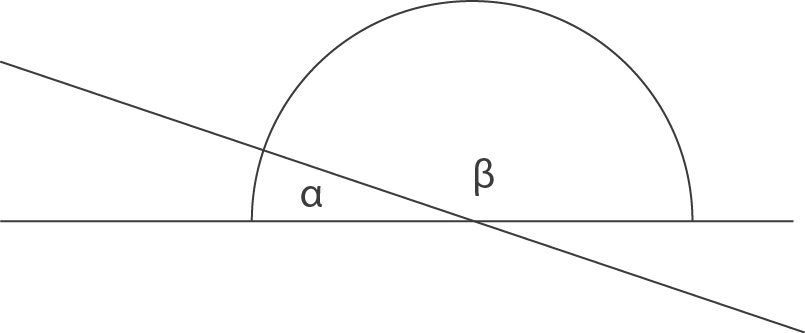
Sie sehen zwei sich schneidende Geraden. Beschreiben Sie, wie Sie den Winkel $\beta$ berechnen.

Diagramm mit einem Halbkreis und zwei Winkeln, α und β, sowie einer schrägen Linie.

8.

Zwei Strahler sind zum Himmel gerichtet. Strahler $S_1$ beginnt im Punkt $P\left(1\mid 2\mid 0\right)$ und strahlt in Richtung des Vektors

$\overrightarrow{v}=\left(\begin{array}{r} 3\\ 2\\ 3\\ \end{array}\right)$ .

Strahler $S_2$ beginnt im Punkt $Q\left(-1\mid 1\mid 0\right)$ und kreuzt den Strahl von $S_1$ im Punkt $T\left(16\mid 12\mid 15\right)$ .

Unter welchem Winkel schneiden sich die beiden Strahler?

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.

$E$ und $F$ - Normalenvektoren ablesen

$\overrightarrow{n}_E$ = $\left(\begin{array}{r} 0\\ 2\\ 1\\ \end{array}\right)$

$\overrightarrow{n}_F$ = $\left(\begin{array}{r} -3\\ 1\\ -1\\ \end{array}\right)$

$\begin{array}\\cos\alpha&=&\dfrac{1}{\sqrt{55}}\end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\cos^{-1}\left(\dfrac{1}{\sqrt{55}}\right)\approx82,25^{\circ}$

$E$ und $G$ - Normalenvektor bestimmen

$\overrightarrow{n}_G=\left(\begin{array}{r} 3\\ 1\\ -1\\ \end{array}\right)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\begin{array}\\cos\beta&=&\dfrac{1}{\sqrt{55}}\end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\cos^{-1}\left(\dfrac{1}{\sqrt{55}}\right)\approx82,25^{\circ}$

Damit ist die Gleichheit der Schnittwinkel nachgewiesen.

2.

Normalenvektoren bestimmen - Kreuzprodukt der Richtungsvektoren der Geraden

$\overrightarrow{n}_E$ = $\left(\begin{array}{r} 1\\ -1\\ 3\\ \end{array}\right)$

$\overrightarrow{n}_F=\left(\begin{array}{r} 3\\ -5\\ 1\\ \end{array}\right)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\begin{array}{rcll} \cos\alpha=\dfrac{11}{\sqrt{385}} \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\cos^{-1}\left(\dfrac{11}{\sqrt{385}}\right)\approx55,9^{\circ}$

3.

Ebene $ABC$ - Verbindungsvektoren aufstellen

$\overrightarrow{AB}$ = $\left(\begin{array}{r} 2-1\\ 1-2\\ -2-1\\ \end{array}\right)$ = $\left(\begin{array}{r} 1\\ -1\\ -3\\ \end{array}\right)$

$\overrightarrow{BC}$ = $\left(\begin{array}{r} 3-2\\ 0-1\\ 4-(-2)\\ \end{array}\right)$ = $\left(\begin{array}{r} 1\\ -1\\ 6\\ \end{array}\right)$

Ebene $ABC$ - Normalenvektor bestimmen}

$\overrightarrow{n}_{ABC}=\left(\begin{array}{r} -9\\ -9\\ 0\\ \end{array}\right)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Ebene $ABD$ - Verbindungsvektoren aufstellen

$\overrightarrow{AD}$ = $\left(\begin{array}{r} 4-1\\ 4-2\\ 2-1\\ \end{array}\right)$ = $\left(\begin{array}{r} 3\\ 2\\ 1\\ \end{array}\right)$

Ebene $ABD$ - Normalenvektor bestimmen

$\overrightarrow{n}_{ABD}=\left(\begin{array}{r} 5\\ -10\\ 5\\ \end{array}\right)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\begin{array}\\cos\alpha=\dfrac{45}{\sqrt{24300}}\end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\cos^{-1}\left(\dfrac{45}{\sqrt{24300}}\right)\approx73,22^{\circ}$

4.

Parameter $k$ bestimmen

$\sin(60^{\circ})=\dfrac{1}{2}\sqrt3$

Diesen Wert kann man der Formelsammlung entnehmen.

Der Normalenvektor der Ebene ist $\overrightarrow{n}_E$ = $\left(\begin{array}{r} 0\\ 1\\ 1\\ \end{array}\right)$ .

$k=2$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Die Gerade

$g_2:\overrightarrow{x}$ = $\left(\begin{array}{r} 1\\ 3\\ 2\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 1\\ 2\\ 1\\ \end{array}\right)$ schneidet die Ebene $E$ unter einem Winkel von $60^{\circ}$ .

5.

$E$ und $x_1$ -Achse

Der Normalenvektor von $E$ lautet $\overrightarrow{n}_E$ = $\left(\begin{array}{r} 2\\ 2\\ -1\\ \end{array}\right)$ , der Richtungsvektor der $x_1$ -Achse lautet $\overrightarrow{v}_{x_1}$ = $\left(\begin{array}{r} 1\\ 0\\ 0\\ \end{array}\right)$

$\begin{array}\\sin&\alpha&=&\dfrac{2}{3}\end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\sin^{-1}\left(\dfrac{2}{3}\right)\approx41,81^{\circ}$

$E$ und $x_2$ -Achse

Der Richtungsvektor der $x_2$ -Achse lautet $\overrightarrow{v}_{x_1}$ = $\left(\begin{array}{r} 0\\ 1\\ 0\\ \end{array}\right)$

$\begin{array}\\sin&\beta&=&\dfrac{2}{3}\end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\sin^{-1}\left(\dfrac{2}{3}\right)\approx41,81^{\circ}$

$E$ und $x_3$ -Achse

Der Richtungsvektor der $x_3$ -Achse lautet $\overrightarrow{v}_{x_3}$ = $\left(\begin{array}{r} 0\\ 0\\ 1\\ \end{array}\right)$

$\begin{array}\\sin&\gamma&=&\dfrac{1}{3}\end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\sin^{-1}\left(\dfrac{1}{3}\right)\approx19,47^{\circ}$

6.

Punkt $E$ bestimmen: $\Rightarrow$ Aus dem Schaubild ergibt sich $\;E(6|0|4)$

Gerade $g_{EG}$ bestimmen:

$g_{EG}:\;\overrightarrow{x}$ = $\overrightarrow{E} +r\cdot\overrightarrow{EG}$

$\overrightarrow{x}$ = $\left( {\begin{array}{*{20}r} 6 \\ 0 \\ 4 \\ \end{array}} \right)+ r\left( {\begin{array}{*{20}r} -6 \\ 6 \\ 0 \\ \end{array}} \right)$

Gerade $g_{GS}$ bestimmen:

$g_{GS}:\;\overrightarrow{x}$ = $\overrightarrow{G} + s\cdot\overrightarrow{GS}$

$\overrightarrow{x}$ = $\left( {\begin{array}{*{20}r} 0 \\ 6 \\ 4 \\ \end{array}} \right)+ s\left( {\begin{array}{*{20}r} 3 \\ -3 \\ 5 \\ \end{array}} \right)$

Für den Schnittwinkel berechnen wir:

$\begin{array}{rcll} \cos \alpha &=& \frac{{\left| {\left( {\begin{array}{*{20}r} -6 \\ 6 \\ 0 \\ \end{array}} \right) \cdot \left( {\begin{array}{*{20}r} 3 \\ -3 \\ 5 \\ \end{array}} \right)} \right|}}{{\left| {\left( {\begin{array}{*{20}r} -6 \\ 6 \\ 0 \\ \end{array}} \right)} \right| \cdot \left| {\left( {\begin{array}{*{20}r} 3 \\ -3 \\ 5 \\ \end{array}} \right)} \right|}}\\ \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\Rightarrow \cos^{-1}\left(\dfrac{36}{\sqrt{3096}}\right)\approx49,68^{\circ}$

7.

Berechnung von $\beta$ beschreiben

Wir kennen eine Formel zur Bestimmung des Schnittwinkels zweier Geraden. Wenn $\overrightarrow{u}$ und $\overrightarrow{v}$ die Richtungsvektoren der beiden Geraden sind, dann gilt für den Cosinus ihres Schnittwinkels:

$\cos\alpha$ = $\dfrac{\left|\overrightarrow{u}\circ\overrightarrow{v}\right|}{\left|\overrightarrow{u}\right|\cdot\left|\overrightarrow{v}\right|}$ .

Nun sind im Bild jedoch zwei Schnittwinkel zu sehen, nämlich der spitze Winkel $\alpha$ und der stumpfe Winkel $\beta$ .

Mit der Formel von oben bestimmen wir immer den kleineren der beiden Schnittwinkel, also $\alpha$ .

Wir können mit der Formel also $\alpha$ bestimmen. Wie wir in der Darstellung sehen können, bilden $\alpha$ und $\beta$ zusammen einen Winkel von $180^{\circ}$ . Für $\beta$ gilt also:

$\beta=180^{\circ}-\alpha$ .

8.

Geradengleichungen bestimmen

Wir stellen die beiden Lichtstrahlen als Geraden dar.

Strahler $S_1$

Er beginnt im Punkt $P\left(1\mid 2\mid 0\right)$ ; der Richtungsvektor des Lichtstrahls ist $\overrightarrow{v}=\left(\begin{array}{r} 3\\ 2\\ 3\\ \end{array}\right)$ :

$S_1:\overrightarrow{x}$ = $\left(\begin{array}{r} 1\\ 2\\ 0\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 3\\ 2\\ 3\\ \end{array}\right)$ .

Strahler $S_2$

Er verläuft durch die Punkte $Q\left(-1\mid 1\mid 0\right)$ und $T\left(16\mid 12\mid 15\right)$ :

$\begin{array}{rcll} S_2:\overrightarrow{x}&=&\overrightarrow{Q}+s\cdot\overrightarrow{QT}\\ \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Schnittwinkel der Geraden bestimmen

$\begin{array}{rll} \cos\alpha&=&\dfrac{\left|\left(\begin{array}{r} 3\\ 2\\ 3\\ \end{array}\right)\circ\left(\begin{array}{r} 17\\ 11\\ 15\\ \end{array}\right)\right|}{\left|\left(\begin{array}{r} 3\\ 2\\ 3\\ \end{array}\right)\right|\cdot\left|\left(\begin{array}{r} 17\\ 11\\ 15\\ \end{array}\right)\right|}\\ \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\cos^{-1}\left(\dfrac{118}{\sqrt{13970}}\right)\approx3,29^{\circ}$ .

Die Lichtstrahlen schneiden sich unter einem Winkel von $3,29^{\circ}$ .

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?