Beschränktes Wachstum
Beim beschränkten Wachstum handelt es sich um ein mathematisches Modell, welches durch eine natürliche Schranke nach oben oder unten begrenzt wird, diese wird oft auch als Kapazität oder Sättigung bezeichnet. Dieses Modell wird beispielsweise für Wachstumsprozesse des Marktanteils, die Populationsausbreitung in einem begrenzten Raum oder auch Erwärmungs-/Abkühlprozesse verwendet.
hat die allgemeine Gleichung:
=
=
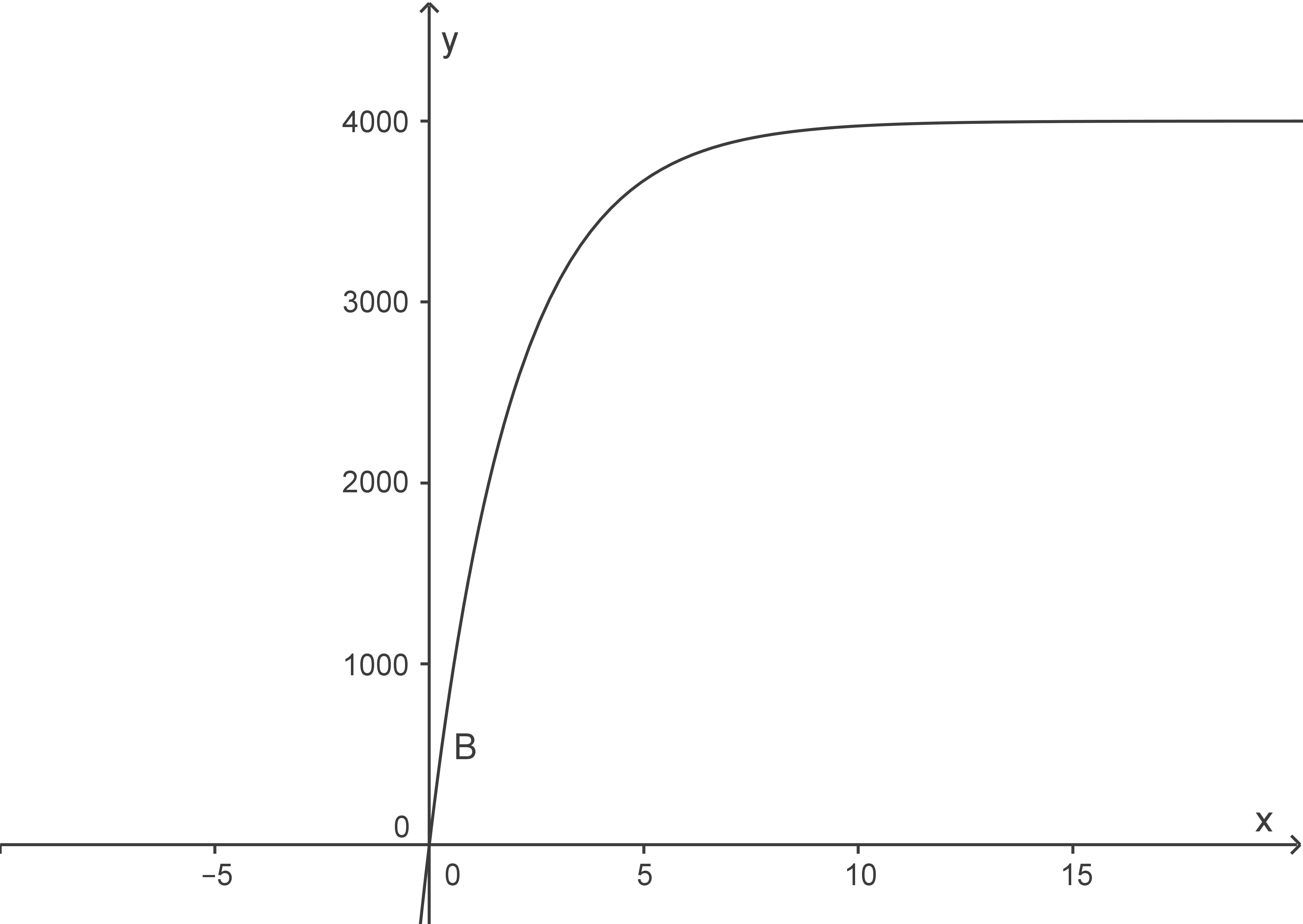Das nach unten beschränkte Wachstum mit 
hat die allgemeine Gleichung:
=
=
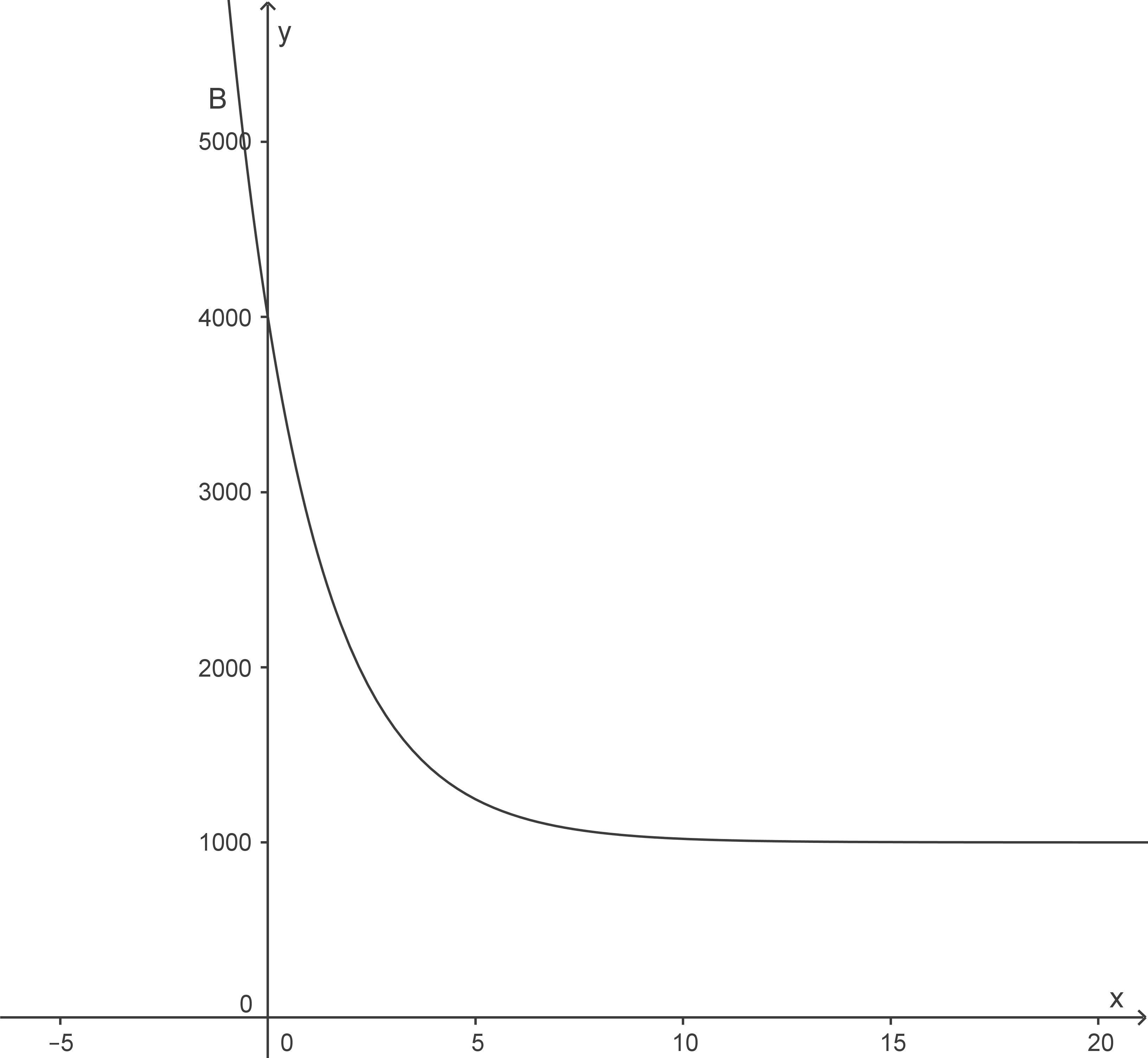Dabei gilt folgendes für die Parameter:
) des Verkaufs hat noch niemand diese Zeitschrift, ist 
. Die Schranke (Sättigung) entspricht der Anzahl der Haushalte: 
. Für die Anzahl der verkauften Zeitschriften wird folgende Funktion aufgestellt.
Dabei ist 
die Zeit in Wochen nach Verkaufsbeginn. Die Wachstumskonstante 
kannst du mit der Anzahl der nach 
Woche verkauften Zeitschriften berechnen:
Die Wachstumsfunktion lautet somit: 
.
Der Verlag möchte gerne wissen, wann in 75% der Haushalte die Zeitschrift zu finden ist.
75% der Haushalte entspricht 3000 Haushalte. Es ist also der Zeitpunkt gesucht, für den 
gilt.
Nach ungefähr drei Wochen haben 75% der Haushalte die Zeitschrift gekauft.
Modell
Das nach oben beschränkte Wachstum mit
- t: Zeit
: Anfangsbestand
: Bestandsgröße nach
: natürliche Schranke
Beispiel
Ein Verlag bringt in einer Stadt eine neue Zeitschrift auf den Markt. Die Stadt hat 4000 Haushalte und nach einer Woche sind 1436 Zeitschriften verkauft. Der Verkauf der Zeitschrift soll als begrenztes Wachstum modelliert werden. Zu Beginn (
\begin{array}{rlll} k& \approx&0,445 \end{array}
Vollständige Lösung anzeigen
Aufgabe 1
In einem Amazonas-Gebiet werden neue Bäume gepflanzt. Das Gebiet umfasst eine Größe für ca. 5.000 Bäume. 500 Bäume werden angepflanzt. Es wird erwartet, dass sich in zwei Jahren 700 Bäume auf diesem Gebiet befinden.
a)
Ermittle eine Funktionsgleichung, mit der sich das Ausbreiten der Bäume beschreiben lässt.
b)
Wann werden sich 2.000 Bäume auf dem Gebiet befinden? Wann 3.000?
Aufgabe 2
In der Wüste von Dubai wird ein neuer Rennwagen getestet, der eine Spitzengeschwindigkeit von 468 Stundenkilometern fährt. Nach 3 Sekunden hat er bei optimalen Verhältnissen 100 Stundenkilometer erreicht.
a)
Ermittle anhand dieser Daten eine Funktionsgleichung, mit der sich die Geschwindigkeitsentwicklung des Wagens beschreiben lässt.
b)
Wann hat er 300 Stundenkilometer erreicht? Wann 400?
c)
Zu welchem Zeitpunkt hat die erste Ableitung den Wert 10? Wie ist dies in diesem Kontext zu interpretieren?
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
a)
Da es sich um beschränktes Wachstum handelt, lautet die allgemeine Wachstumsgleichung:
1. Schritt: bestimmen
Da 
die obere Schranke darstellt, muss 
sein.
2. Schritt: 
bestimmen
Es gilt 
, damit lässt sich berechnen:
![\( \begin{array}{rlllllll}
500&=5000-a\mathrm e^{-k\cdot0}\\[3pt]
500&=5000-a\cdot1\quad\scriptsize\mid\; -5000\\[3pt]
-4500&=-a \quad\scriptsize\mid\;\cdot\left(-1\right)\\[3pt]
4500&=a
\end{array}\)](https://mathjax.schullv.de/2776b3985fcea640adfc1e6b25b1253be966ccafce263693a78590144aea2ae6?color=5a5a5a)
3. Schritt: bestimmen
![\( \begin{array}{rlll}
700&=&5000-4500\mathrm e^{-2k}\quad\scriptsize\mid\; -5000\\[5pt]
-4300&=&-4500\mathrm e^{-2k}\quad\scriptsize\mid\; :\left(-4500\right)\\[5pt]
\dfrac{43}{45}&=&\mathrm e^{-2k}\quad\scriptsize\mid\; \ln{\left(\;\right)}\\[5pt]
\ln{\left(\dfrac{43}{45}\right)}&=&\ln{\left(\mathrm e^{-2k}\right)}\\[5pt]
\ln{\left(\dfrac{43}{45}\right)}&=&-2k\quad\scriptsize\mid\; :\left(-2\right)\\[5pt]
\dfrac{\ln{\left(\dfrac{43}{45}\right)}}{-2}&=&k\\[5pt]
0,0227&\approx& k
\end{array}\)](https://mathjax.schullv.de/d8a82057e495aebb9928c61437610e260ff51969a7fac4affabdf71fd7b3c912?color=5a5a5a)
Daraus ergibt sich folgende Funktionsgleichung:
b)
Zeitpunkt für 2.000 Bäume berechnen
![\(\begin{array}[t]{rll}
B(t)&=&2000 \\[5pt]
5000-4500\mathrm e^{-0,0227t}&=&2000 \\[5pt]
3000&=&4500\mathrm e^{-0,0227t} \\[5pt]
\dfrac{2}{3}&=&\mathrm e^{-0,0227t} \\[5pt]
\ln\left(\dfrac{2}{3}\right)&=&-0,0227t \\[5pt]
t&\approx&17,86
\end{array}\)](https://mathjax.schullv.de/8f55867083910f311c4f7d2c6f245c976c2bbf507d7ec81d6dd4bfa3197ed930?color=5a5a5a)
Zeitpunkt für 3.000 Bäume berechnen
![\(\begin{array}[t]{rll}
B(t)&=&3000 \\[5pt]
5000-4500\mathrm e^{-0,0227t}&=&3000 \\[5pt]
2000&=&4500\mathrm e^{-0,0227t} \\[5pt]
\dfrac{4}{9}&=&\mathrm e^{-0,0227t} \\[5pt]
\ln\left(\dfrac{4}{9}\right)&=&-0,0227t \\[5pt]
t&\approx&35,72
\end{array}\)](https://mathjax.schullv.de/b312874621de5194e0b36c522e58efaca8fce348227a67164daaa3811ebcac32?color=5a5a5a)
Lösung 2
a)
Da es sich um beschränktes Wachstum handelt, lautet die allgemeine Wachstumsgleichung:
1. Schritt: bestimmen
Da die obere Schranke darstellt, muss 
sein.
2. Schritt: bestimmen
Es gilt \(B(0)=0\), damit lässt sich \(a\) berechnen:
![\( \begin{array}{rlllllll}
0&=468-a\mathrm e^{-k\cdot0}\\[3pt]
0&=468-a\cdot1\quad\scriptsize\mid\; +a\\[3pt]
a&=468
\end{array}\)](https://mathjax.schullv.de/c1868870781c2c495e07276c81bc84b726099f4aed44f618767bc0d0f84ab420?color=5a5a5a)
3. Schritt: bestimmen
![\( \begin{array}{rlll}
468-468\mathrm e^{-3k}&=&100\\[5pt]
368&=&468\mathrm e^{-3k}\\[5pt]
\dfrac{92}{117} &=&\mathrm e^{-3k}\\[5pt]
\ln{\left(\dfrac{92}{117}\right)}&=&\ln{\left(\mathrm e^{-3k}\right)}\\[5pt]
\ln{\left(\dfrac{92}{117}\right)}&=&-3k\\[5pt]
\dfrac{\ln{\left(\dfrac{92}{117}\right)}}{-3}&=&k\\[5pt]
k &\approx& 0,0801
\end{array}\)](https://mathjax.schullv.de/38c176c66bef57cf1b470f1ac4caca410cf27b110a1efb119fde62b97d2498b5?color=5a5a5a)
Daraus ergibt sich die Wachstumsgleichung:
b)
Zeitpunkt für 300 Stundenkilometer berechnen
![\(\begin{array}[t]{rll}
468-468\mathrm e^{-0,0801t}&=&300 \\[5pt]
168&=&468\mathrm e^{-0,0801t} \\[5pt]
\dfrac{14}{39}&=&\mathrm e^{-0,0801t}\\[5pt]
\ln\left({\dfrac{14}{39}}\right)&=&-0,0801t\\[5pt]
\dfrac{\ln\left({\dfrac{14}{39}}\right)}{-0,0801}&=&t\\[5pt]
t&\approx&12,79
\end{array}\)](https://mathjax.schullv.de/6af7b3028a43e8f3c74db74bdcfa5d9edc2ce13c4ed51f64e11431b68443586c?color=5a5a5a)
Nach ca. 13 Sekunden hat der Wagen 300 Stundenkilometer erreicht.
Zeitpunkt für 400 Stundenkilometer berechnen
![\(\begin{array}[t]{rll}
468-468\mathrm e^{-0,0801t}&=&400 \\[5pt]
68&=&468\mathrm e^{-0,0801t} \\[5pt]
\dfrac{17}{117}&=&\mathrm e^{-0,0801t}\\[5pt]
\ln\left({\dfrac{17}{117}}\right)&=&-0,0801t\\[5pt]
\dfrac{\ln\left({\dfrac{17}{117}}\right)}{-0,0801}&=&t\\[5pt]
t&\approx&24,08
\end{array}\)](https://mathjax.schullv.de/b7861cb4dc715bed6d0c46f10be9d88f0cfaeba7957a0f83ad9d1a886c460d70?color=5a5a5a)
Nach etwa 24,08 Sekunden hat der Wagen 400 Stundenkilometer erreicht.
c)
1. Schritt: Ableitungsfunktion aufstellen
2. Schritt: 
setzen und nach auflösen
![\( \begin{array}[t]{rlll}
37,4868\mathrm e^{-0,0801t}&=&10\\[5pt]
\mathrm e^{-0,0801t}&=&0,266760566\\[5pt]
-0,0801t&=&\ln{\left(0,266760566\right)}\\[5pt]
t&=&\dfrac{\ln{\left(0,266760566\right)}}{-0,0801}\\[5pt]
t&\approx&16,5
\end{array}\)](https://mathjax.schullv.de/1835904cf09d8c99f24bbf55d5510be9c942a21fb84c1184e3e1efb8ee97ba77?color=5a5a5a)
3. Schritt: Wert interpretieren
Die Ableitung gibt immer die Änderungsrate an. Die Änderungsrate der Geschwindigkeit ist die Beschleunigung. Wenn die erste Ableitung 10 beträgt, beschleunigt der Wagen in dieser Sekunde also um 10 Stundenkilometer.