Ganzrationale Funktionen

Ganzrationale Funktionen sind Polynomfunktionen, also Funktionen der Form:

$f(x)$ = $a_n\cdot x^n + a_{n-1}\cdot x^{n-1}$ + $…$ + $a_1 \cdot x+a_0$

Zum Skizzieren des Graphen kannst du entweder eine Wertetabelle anlegen oder dich an einer Grundfunktion orientieren.

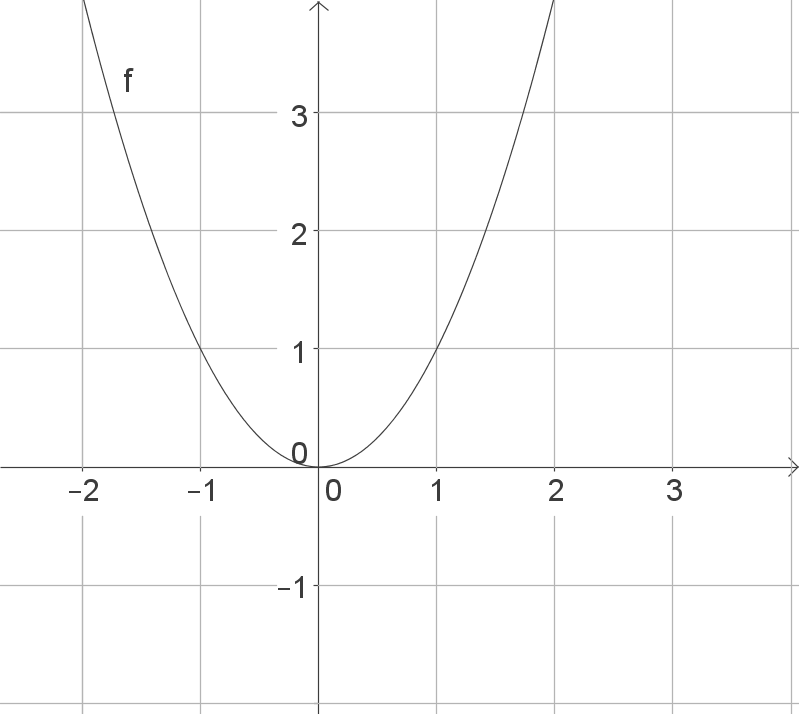
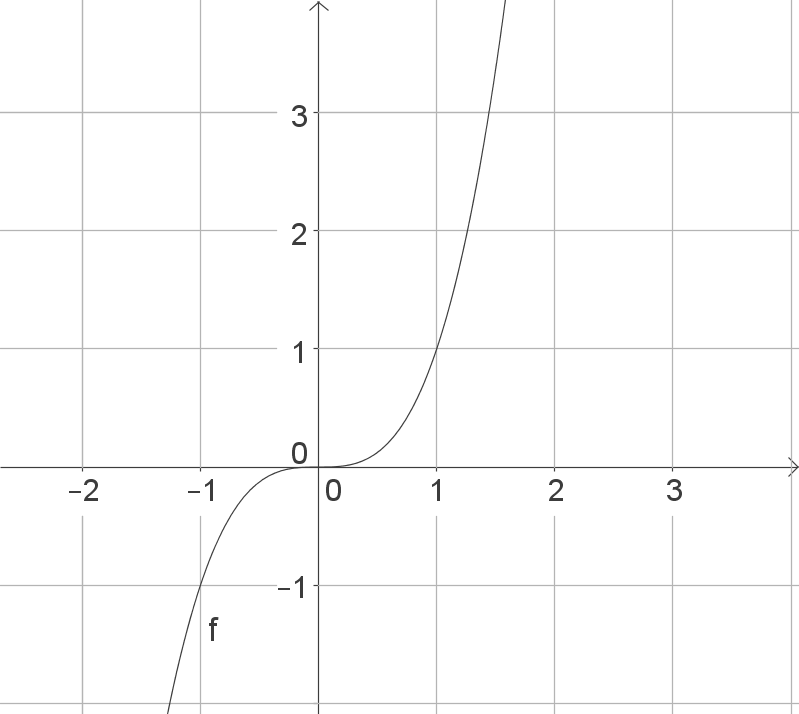
Grundfunktionen

Merke dir die Graphen der einfachsten Polynome, um daraus den Graph der jeweiligen Funktion abzuleiten.

$f(x) = a$ : Parallele zur $x$ -Achse:

Koordinatensystem mit Achsen und Rasterlinien, ohne spezifische Daten oder Funktionen.

$f(x) = x$ : Gerade durch den Nullpunkt:

Koordinatensystem mit einer positiven Diagonalen und Achsenbeschriftungen.

$f(x) = x^2$ : Normalparabel

Graph einer Parabel mit Achse und Koordinatensystem.

$f(x) = x^3$ :

Graf einer Funktion mit Achsen und Gitterlinien, zeigt verschiedene Werte auf der x- und y-Achse.

Skizziere die Schaubilder folgender Funktionen und bestimme die Schnittpunkte mit den Koordinatenachsen.

$f(x)=\frac{1}{4}x+2$

$f(x)=-2x+4$

$f(x)=x^2-2x+1$

$f(x)=(x-1)^2+2$

$f(x)=(x+1)^3$

$f(x)=x^2-4$

Skizziere das Schaubild der Funktion und beschreibe, wie es aus der Normalparabel hervorgeht.

$f(x)=x^2+2x+1$

$f(x)=-(x-2)^2+2$

$f(x)=x^2-4$

$f(x)=2x^2-2$

$f(x)=3(x+1)^2-2$

$f(x)=-(x+2)^2$

Verschiebe das Schaubild der angegebenen Funktion wie gefordert und gib die Funktionsgleichung der neuen Funktion an.

$f(x)=2x$

Verschiebung um 3 LE in positive x-Richtung und um 2 LE in positive y-Richtung

$f(x)=x^2$

Verschiebung um 2 LE in negative x-Richtung und um 1 LE in positive y-Richtung

$f(x)=x^3$

Verschiebung um 1 LE in negative x-Richtung und um 4 LE in negative y-Richtung

$f(x)=3x^2$

Verschiebung um 2 LE in positive y-Richtung und anschließende Spiegelung an der x-Achse

$f(x)=-x^2$

Verschiebung um 3 LE in positive x-Richtung und anschließende Spiegelung an der x-Achse

$f(x)=-x^3$

Verschiebung um 4 LE in positive y-Richtung und um 3 LE in negative x-Richtung

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$f(x)=\frac{1}{4} \cdot x + 2$

Skizze

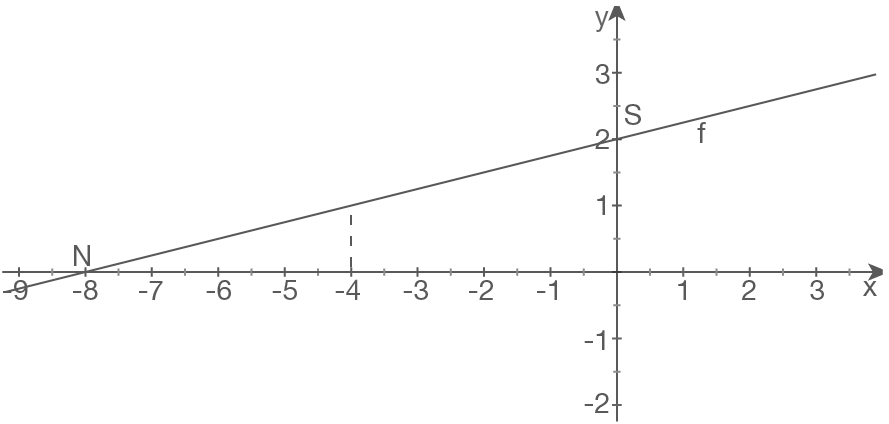
Graph einer linearen Funktion mit Achsen und Bezugspunkten.

Schnittpunkte mit den Koordinatenachsen bestimmen

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse: $f(x) = 0$ setzen

$\frac{1}{4}x+2=-8$

Vollständige Lösung anzeigen

Daraus folgt der Schnittpunkt $N(-8 \mid 0)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse: $x = 0$ setzen

$\frac{1}{4}\cdot0+2=2$

Daraus folgt der Schnittpunkt $S\left(0\mid2\right)$ .

$f(x)=-2 \cdot x + 4$

Skizze

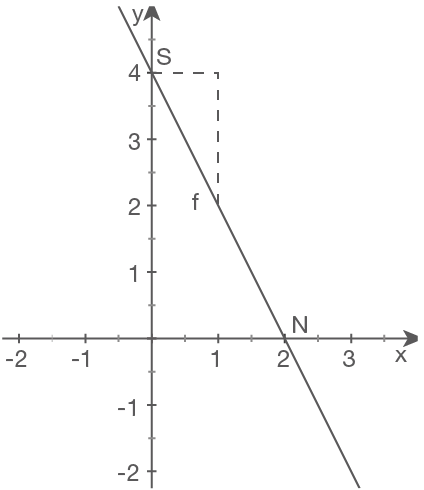
Graph eines linearen Funktionsverlaufs im Koordinatensystem mit Achsenbeschriftung.

Schnittpunkte mit den Koordinatenachsen bestimmen

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse: $f(x) = 0$ setzen

$-2x+4=2$

Vollständige Lösung anzeigen

Daraus folgt der Schnittpunkt $N(2 \mid 0)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse: $x = 0$ setzen

$\begin{array}{rll} -2\cdot0+4=&4 \end{array}$

Daraus folgt der Schnittpunkt $S\left(0\mid4\right)$ .

$f(x)=x^2-2x+1$

Skizze

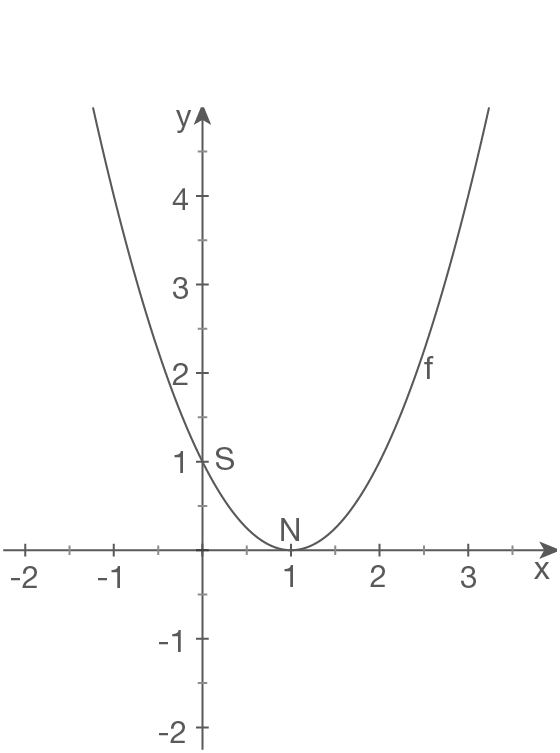
Graph einer Parabel mit Achsenbeschriftungen und Markierungen für S und N.

Schnittpunkte mit den Koordinatenachsen bestimmen

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse: $f(x) = 0$ setzen

$x^2-2x+1=1$

Vollständige Lösung anzeigen

Daraus folgt der Schnittpunkt $N(1 \mid 0)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse: $x = 0$ setzen

$\begin{array}{rll} 0^2-2\cdot0+1=&1 \end{array}$

Daraus folgt der Schnittpunkt $S\left(0\mid1\right)$ .

$f(x)=(x-1)^2+2$

Skizze

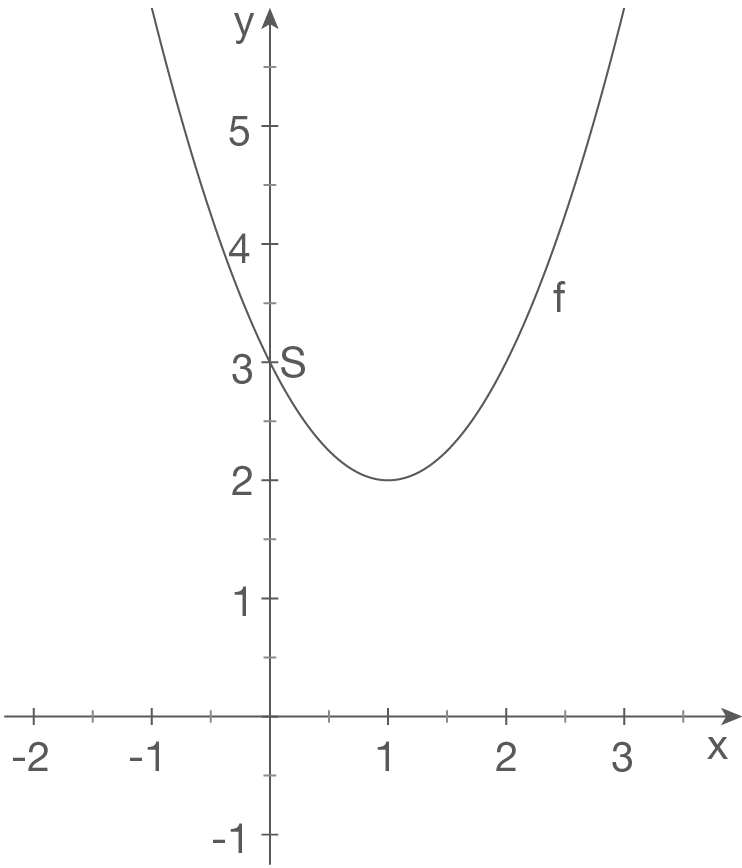
Graph einer Parabel mit Scheitelpunkt S bei (0,3) im Koordinatensystem.

Schnittpunkte mit den Koordinatenachsen bestimmen

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse: $f(x) = 0$ setzen

$(x-1)^2+2=-2$ $\qquad$

Vollständige Lösung anzeigen

Es gibt keinen Schnittpunkt mit der $x$ -Achse.

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse: $x = 0$ setzen

$\begin{array}{rll} (-1)^2+2=&3 \end{array}$

Daraus folgt der Schnittpunkt $S\left(0\mid3\right)$ .

$f(x)=(x+1)^3$

Skizze

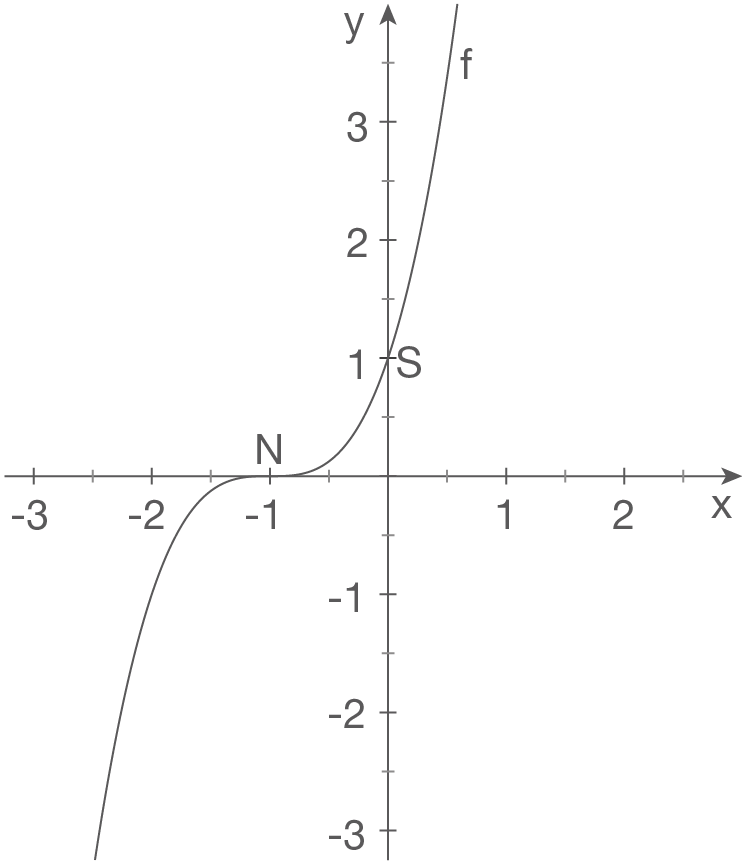
Graph einer Funktion mit Achsenbeschriftungen und markierten Punkten.

Schnittpunkte mit den Koordinatenachsen bestimmen

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse: $f(x) = 0$ setzen

$(x+1)^3=-1$

Vollständige Lösung anzeigen

Daraus folgt der Schnittpunkt $N\left(-1\mid0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse: $x = 0$ setzen

$\begin{array}{rll} 1^3=1 \end{array}$

Daraus folgt der Schnittpunkt $S\left(0\mid1\right)$ .

$f(x)=x^2-4$

Skizze

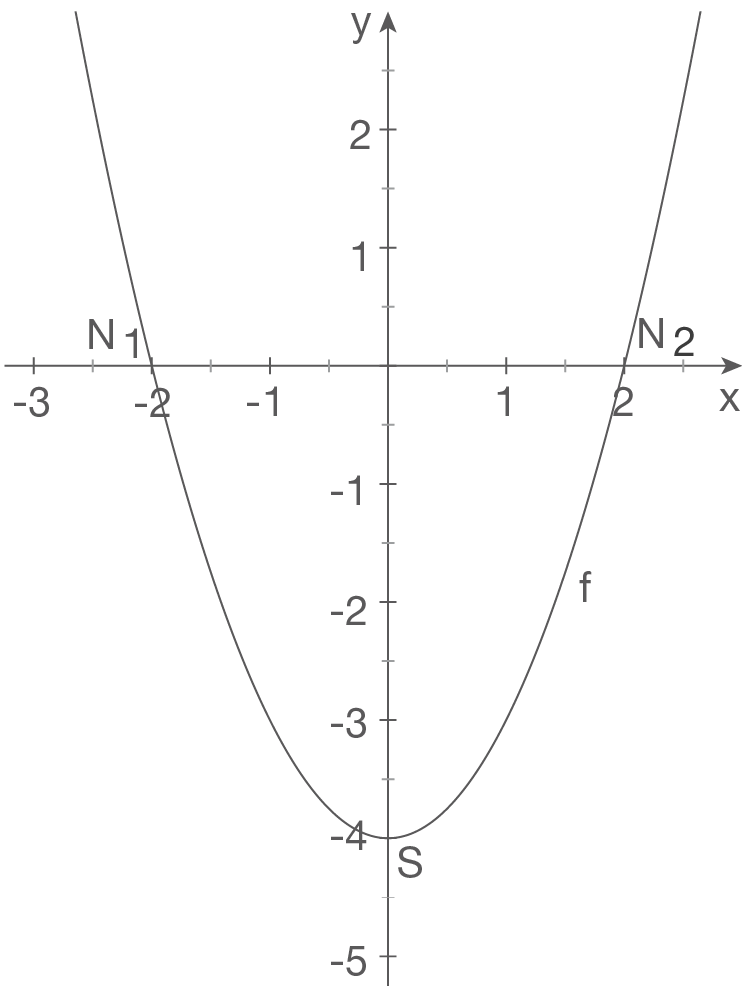
Grafik einer Parabel im Koordinatensystem mit Achsenbeschriftungen.

Schnittpunkte mit den Koordinatenachsen bestimmen

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse: $f(x) = 0$ setzen

$x^2-4=\pm2$

Vollständige Lösung anzeigen

Daraus folgen die Schnittpunkte $N_1\left(-2\mid0\right)$ und $N_2\left(2\mid0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse: $x = 0$ setzen

$\begin{array}{rll} 0^2-4=-4 \end{array}$

Daraus folgt der Schnittpunkt $S\left(0\mid-4\right)$ .

$f(x)=x^2 +2 \cdot x +1$

Skizze

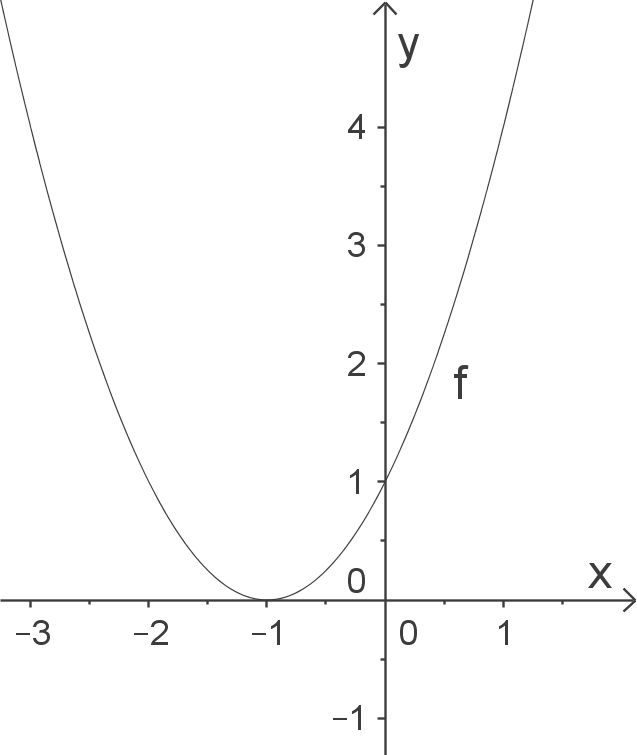
Graf einer Parabel mit den Achsen x und y, zeigt die Funktion f.

Schaubild aus der Normalparabel herleiten

Zunächst schreiben wir die Funktionsgleichung um:

$x^2 + 2 \cdot x + 1$ $=$ $(x+1)^2$ $=$ $\left(x -(-1)\right)^2$

Normalparabel um 1 LE in negative $x$ -Richtung („nach links“) verschoben.

$f(x)=-(x-2)^2 +2$

Skizze

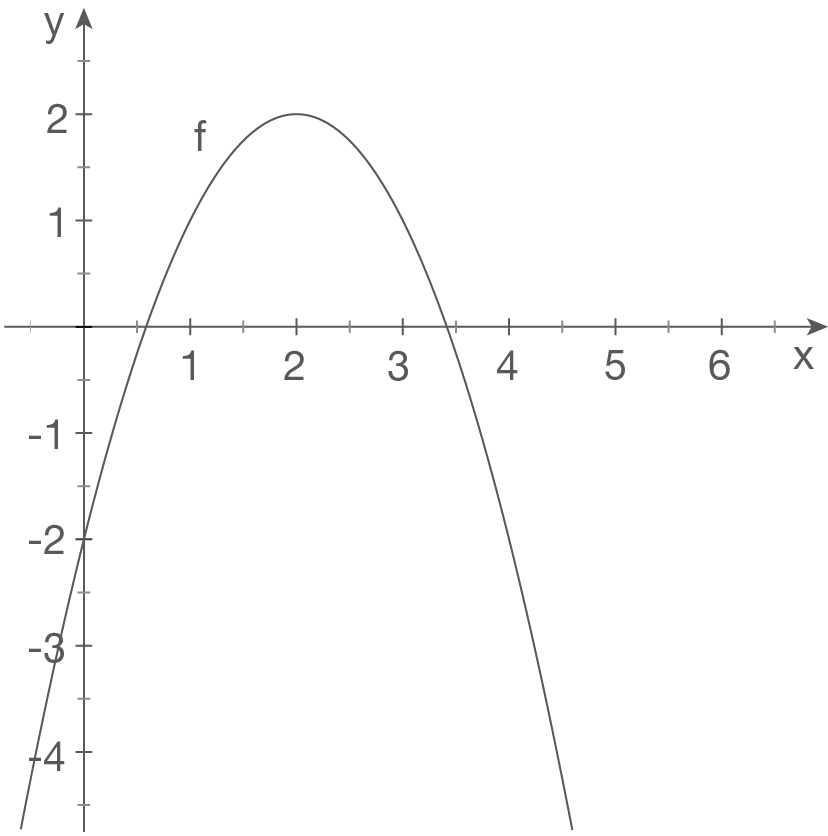
Graf einer Funktion f im Koordinatensystem mit x- und y-Achse.

Schaubild aus der Normalparabel herleiten

Normalparabel um 2 LE in positive $x$ -Richtung („nach rechts“) verschoben, anschließend an der $x$ -Achse gespiegelt und dann um 2 LE in positive $y$ -Richtung („nach oben“) verschoben.

$f(x)=x^2-4$

Skizze

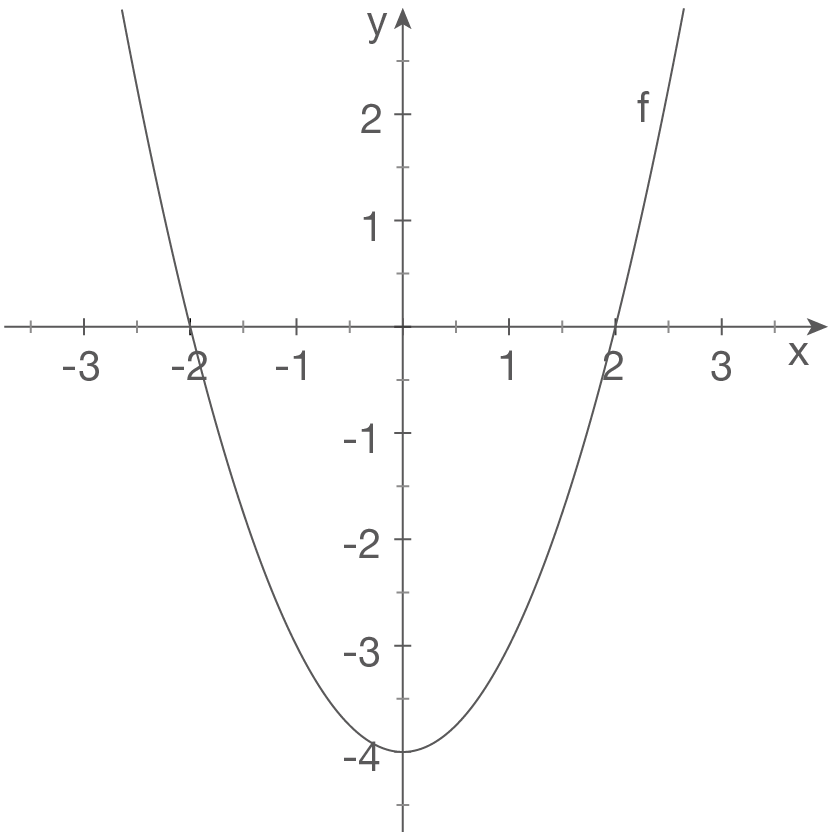
Grafik einer Parabel im Koordinatensystem mit der Funktion f.

Schaubild aus der Normalparabel herleiten

Normalparabel um 4 LE in negative $y$ -Richtung („nach unten“) verschoben.

$f(x)=2 \cdot x^2-2$

Skizze

Graf einer Parabel im Koordinatensystem mit Achsen und beschrifteten Werten.

Schaubild aus der Normalparabel herleiten

Normalparabel um Faktor 2 gestreckt und um 2 LE in negative $y$ -Richtung („nach unten“) verschoben.

$f(x)=3 \cdot \left(x - (-1)\right)^2-2$

Vollständige Lösung anzeigen

Skizze

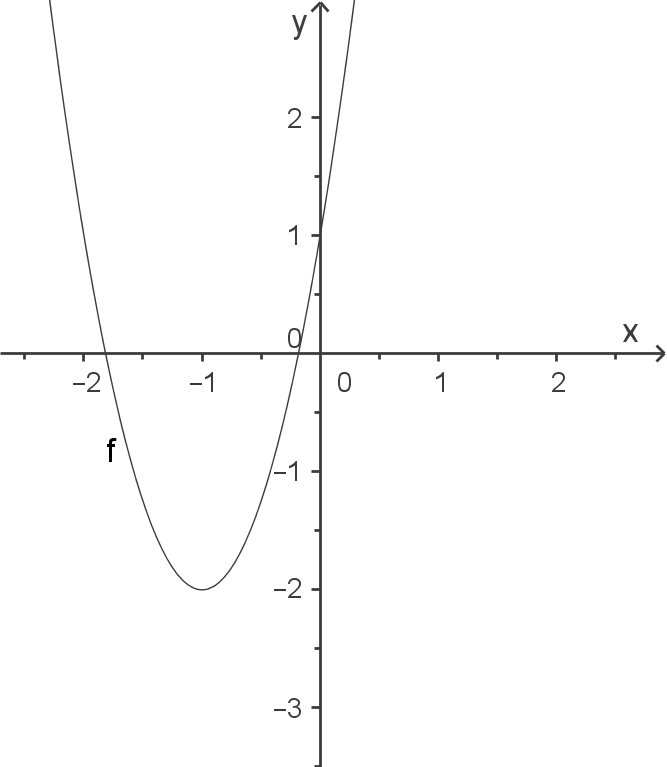Graf einer Parabel mit den Achsen x und y, zeigt den Verlauf einer quadratischen Funktion.

Schaubild aus der Normalparabel herleiten

Normalparabel um 1 LE in negative $x$ -Richtung („nach links“) verschoben, dann um Faktor 3 gestreckt und anschließend um 2 LE in negative $y$ -Richtung („nach unten“) verschoben.

$f(x)-\left(x - (-2)\right)^2-2)$

Vollständige Lösung anzeigen

Skizze

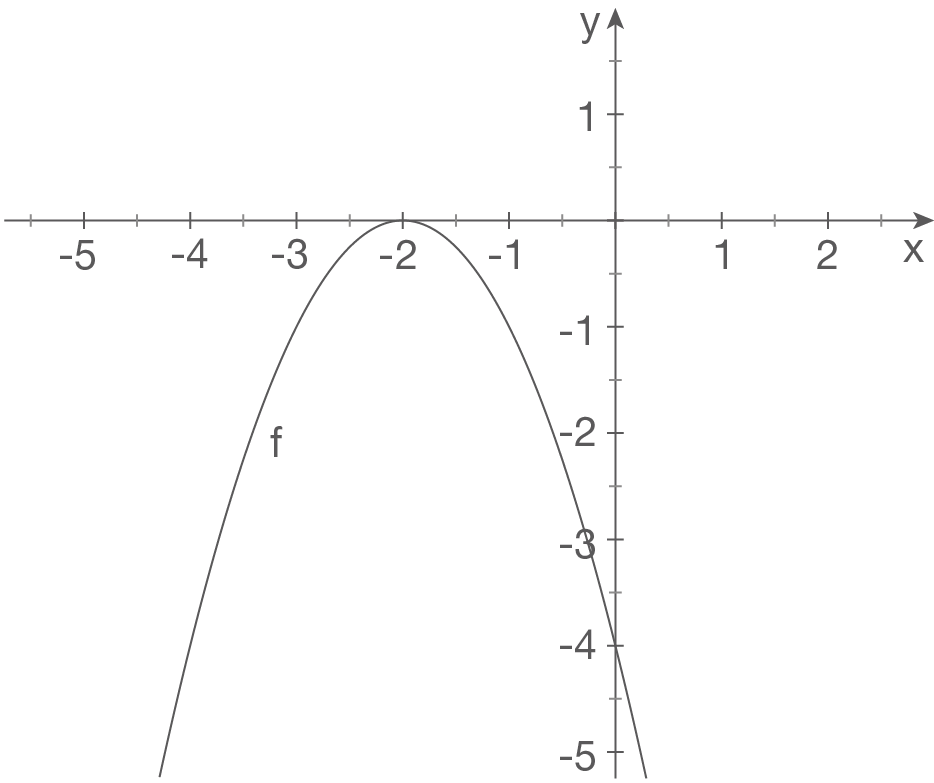Graph einer Funktion f mit einer Parabel, die das Minimum bei x = -2 erreicht. Koordinatensystem dargestellt.

Schaubild aus der Normalparabel herleiten

Normalparabel an der $x$ -Achse gespiegelt und um 2 LE in negative $x$ -Richtung („nach links“) verschoben.

$f(x) = 2 \cdot x$

Verschiebung um 3 LE in positive $x$ -Richtung und um 2 LE in positive $y$ -Richtung.

$f_{neu}(x)=2 \cdot (x-3)+2$

$f(x) = x^2$

Verschiebung um 2 LE in negative $x$ -Richtung und um 1 LE in positive $y$ -Richtung.

$f_{neu}(x)=(x+2)^2+1$

$f(x) = x^3$

Verschiebung um 1 LE in negative $x$ -Richtung und um 4 LE in negative $y$ -Richtung.

$f_{neu}(x)=(x+1)^3-4$

$f(x) = 3 \cdot x^2$

Verschiebung um 2 LE in positive $y$ -Richtung und anschließende Spiegelung an der $x$ -Achse.

$f_{neu}(x)=-\left(3x^2+2\right)$

$f(x) = -x^2$

Verschiebung um 3 LE in positive $x$ -Richtung und anschließende Spiegelung an der $x$ -Achse.

$f_{neu}(x)=(x-3)^2$

$f(x) = -x^3$

Verschiebung um 4 LE in positive $y$ -Richtung und um 3 LE in negative $x$ -Richtung.

$f_{neu}(x)=-(x+3)^3+4$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?