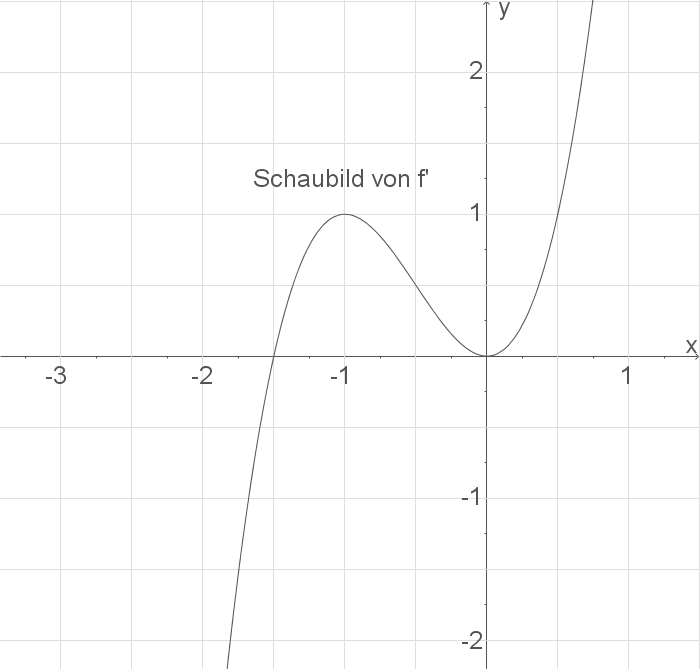
Interpretation von Kurven

Mit der ersten und zweiten Ableitung einer Funktion $f$ kannst du Aussagen über die Funktion $f$ machen.

$f‘(x)$	$f‘‘(x)$	$f$	Anmerkung
für alle $x \in [a,b]$ : $f‘(x) \geq 0$ bzw. $f‘(x) \gt 0$		monoton steigend bzw. streng monoton steigend im Intervall $[a;b]$
für alle $x \in [a,b]$ : $f‘(x)\leq 0$ bzw. $f‘(x) \lt 0$		monoton fallend bzw. streng monoton fallend im Intervall $[a;b]$
Graph verläuft oberhalb der $x$ -Achse		positive Steigung
Graph verläuft unterhalb der $x$ -Achse		negative Steigung
Nullstelle $f‘(x_0) = 0$	$f‘‘(x_0)$ $\lt 0$	lokales Maximum an der Stelle $x_0$	Alternativ zur zweiten Ableitung kannst du auch das Vorzeichenwechsel-Kriterium überprüfen. Wechselt $f‘(x)$ in der Stelle $x_0$ das Vorzeichen von positiv zu negativ, besitzt $f$ bei $x_0$ ein lokales Maximum.
Nullstelle $f‘(x_0) = 0$	$f‘‘(x_0)$ $> 0$	lokales Minimum an der Stelle $x_0$	Alternativ zur zweiten Ableitung kannst du auch das Vorzeichenwechsel-Kriterium überprüfen. Wechselt $f‘(x)$ in der Stelle $x_0$ das Vorzeichen von negativ zu positiv, besitzt $f$ bei $x_0$ ein lokales Minimum.
Nullstelle $f‘(x_0) = 0$ und $f‘(x)$ wechselt in $x_0$ nicht das Vorzeichen		Sattelpunkt an der Stelle $x_0$

Weiter lernen mit SchulLV-PLUS!