Geometrische Interpretation von LGS

Nachdem du ein LGS mit dem Gaußverfahren gelöst hast, ist eine Interpretation der Ergebnisse erforderlich.

Dafür sind allerdings drei unterschiedliche Fälle zu betrachten. Ein lineares Gleichungssystem kann genau eine, keine oder unendlich viele Lösungen besitzen.

$\blacktriangleright$ Gleichungssysteme mit genau einer Lösung

Du hast folgendes Gleichungssystem gegeben:

$\begin{array}[t]{rlllllll} \text{I}\,:& x_1 &+& 4\cdot x_2 &+& x_3 &=& 10 &\quad \scriptsize \; \\[5pt] \text{II}\,:& x_1 &+& 2\cdot x_2 &+& x_3 &=& 8 &\quad \scriptsize \; \\[5pt] \text{III}\,:& x_1 &+& x_2 &-& x_3 &=& 3 &\quad \scriptsize \; \\[5pt] \end{array}$

Verwendest du die Matrixschreibweise, löst du das LGS mit dem Gaußschen Eliminierungsverfahren, indem du die Vorfaktoren als Einträgt für die Matrix benutzt. Falls du Probleme mit dem Lösen hast, bearbeite das zugehörige Kapitel.

$\begin{array}[t]{rlllll} \left(\begin{array}{ccc|c} 1 & 4 & 1 & 10 \\ 1 & 2 & 1 & 8 \\ 1 & 1 & -1 & 3 \\ \end{array}\right)&\rightarrow& \left(\begin{array}{ccc|c} 1 & 4 & 1 & 10 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 2 \\ \end{array}\right) &\rightarrow& \left(\begin{array}{ccc|c} 1 & 0 & 0 & 4 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 2 \\ \end{array}\right) &\quad \scriptsize \; \\[5pt] \end{array}$

Du erhälst die Lösung $x_3=2$ , $x_2=1$ und $x_1=4$ . Diese Lösung ist eindeutig und beschreibt den Punkt $S\,(4 \mid 1 \mid 2)$ . $S$ ist der einzige Punkt, welcher alle drei Gleichungen unabhängig von einander löst.

Die geometrsiche Interpretation: Da es sich bei den Gleichungen $\text{I, II und III}$ um Ebenengleichungen in Koordinatenform handelt, ist $S$ der einzige Punkt, welcher in allen drei Ebenen liegt.

Da nur dieser Punkt existiert ist er ein Schnittpunkt der drei Ebenen.

Abstrakte geometrische Formen in verschiedenen Farben, die sich überlappen und ein modernes Design schaffen.

Abb. 1: Eindeutige Lösung

$\blacktriangleright$ Gleichungssysteme mit unendlich vielen Lösungen

Die zweite Möglichkeit, welche dir das Gaußsche Eliminierungsverfahren an Ergebnissen liefert, ist dass das LGS unendliche viele Lösungen hat:

$\begin{array}[t]{rlll} \left(\begin{array}{ccc|c} 0 & 2 & 6 & 2 \\ 1 & 2 & 2 & 8 \\ 0 & 3 & 9 & 3 \\ \end{array}\right)&\rightarrow& \left(\begin{array}{ccc|c} 1 & 2 & 2 & 8 \\ 0 & 1 & 3 & 1 \\ 0 & 0 & 0 & 0 \\ \end{array} \right)&\quad \scriptsize \; \\[5pt] \end{array}$

In der dritten Gleichung stehen nach dem Gaußverfahren lediglich Nullen. Über die $x_3$ -Koordinate trifft dieses Gleichungssystem keine Aussage. Für diese wählst du eine Variable $t$ . In den übrigen Zeilen steht:

$\begin{array}[t]{rlllllll} \text{I}\,:& x_1 &+& 2\cdot x_2 &+& 2\cdot t &=& 8 &\quad \scriptsize \; \\[5pt] \text{II}\,:& & & x_2 &+& 3\cdot t &=& 1 &\quad \scriptsize \; \\[5pt] \text{III}\,:& & & & & t &=& t &\quad \scriptsize \; \\[5pt] \hline \text{I}\,:& x_1 &+& 2\cdot x_2 &+& 2\cdot t &=& 8 &\quad \scriptsize \; \\[5pt] \text{II}\,:& & & x_2 & & &=& 1-3\cdot t &\quad \scriptsize \; \\[5pt] \text{III}\,:& & & & & t &=& t &\quad \scriptsize \; \\[5pt] \hline \text{I}\,:& x_1 & & & & &=& 6+4\cdot t &\quad \scriptsize \; \\[5pt] \text{II}\,:& & & x_2 & & &=& 1-3\cdot t &\quad \scriptsize \; \\[5pt] \text{III}\,:& & & & & t &=& t &\quad \scriptsize \; \\[5pt] \end{array}$

Du erhälst einen Lösungsvektor $\overrightarrow{x}$ in welchem Terme mit $t$ und konstante Terme stehen.

$\overrightarrow{x}=\pmatrix{6+4\cdot t \\ 1-3\cdot t \\ t }=\pmatrix{6\\1\\0}+\pmatrix{4\cdot t\\-3\cdot t\\1\cdot t}=\pmatrix{6\\1\\0}+t\cdot\pmatrix{4\\-3\\1}$ .

Du erkennst, dass es sich um eine Geradengleichung handelt. Geometrisch haben die drei Ebenen eine gemeinsam Schnittgerade, welche durch diese Gleichung beschrieben wird.

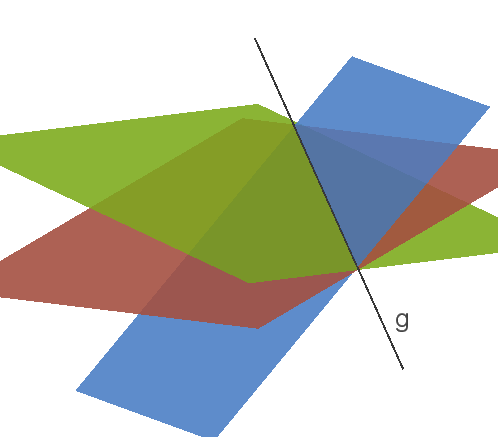Abstrakte Darstellung von überlappenden Flächen in verschiedenen Farben mit einer Linie.

Abb. 2: Unendlich viele Lösungen

$\blacktriangleright$ Gleichungssysteme mit keiner Lösung

Du hast ein Gleichungssystem gegeben, welches du erneut mit dem Gaußschen Eliminierungsverfahren löst:

$\begin{array}[t]{rlllll} \left(\begin{array}{ccc|c} 0 & 2 & 6 & 2 \\ 1 & 2 & 1 & 4 \\ 0 & 3 & 9 & 5 \\ \end{array}\right)&\rightarrow& \left(\begin{array}{ccc|c} 1 & 2 & 1 & 4 \\ 0 & 1 & 3 & 1 \\ 0 & 0 & 0 & 1 \\ \end{array}\right) &\rightarrow& \left(\begin{array}{ccc|c} 1 & 0 & -5 & 0 \\ 0 & 1 & 3 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}\right) &\quad \scriptsize \; \\[5pt] \end{array}$

In der letzten Zeile der Matrix steht $0\cdot x_1+0\cdot x_2+0\cdot x_3=1$ . Dies ist nicht möglich und das Gleichungssystem hat keine Lösung. Geometrisch interpretiert gibt es keinen Punkt und keine Gerade, welche alle drei Ebenen gemeinsam haben.

Grafische Darstellung mit geometrischen Formen in verschiedenen Farben.

Abb. 3: Keine Lösung

Bildnachweise [nach oben]

[1]

[2]

[3]

Du sollst die Lage von Ebenen zueinander untersuchen. Die Gleichungssystem schreibst du dazu in die Matrixform um und löst diese mit dem Gaußschen Eliminierungsverfahren.

$\left(\begin{array}{ccc|c} 1 & 4 & 1 & 10 \\ 1 & 2 & 1 & 8 \\ 1 & 1 & -1 & 3 \end{array}\right)\rightarrow \left(\begin{array}{ccc|c} 1 & 4 & 1 & 10 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 2 \end{array}\right)\rightarrow \left(\begin{array}{ccc|c} 1 & 0 & 0 & 4 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 2 \end{array}\right)$

Du erhälst eine eindeutige Lösung mit $x_1=4$ , $x_2=1$ und $x_3=2$ . Der Punkt $S\,(4\mid 1\mid 2)$ ist der Schnittpunkt der drei Ebenen.

$\left(\begin{array}{ccc|c} 3 & -1 & 2 & 7 \\ 1 & 2 & 3 & 14 \\ 1 & -5 & -4 & 21 \end{array}\right)\rightarrow \left(\begin{array}{ccc|c} 1 & -\frac{1}{3} & \frac{2}{3} & \frac{7}{3} \\ 0 & 1 & 1 & 5 \\ 0 & 0 & 0 & 1 \end{array}\right)\rightarrow \left(\begin{array}{ccc|c} 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$

Die dritte Zeile sorgt dafür, dass das Gleichungssystem keine Lösung besitzt. Die Ebenen müssen dementsprechend parallel zueinander liegen.

$\left(\begin{array}{ccc|c} 4 & -1 & -1 & 0 \\ 3 & 2 & 1 & 10 \\ -8 & 2 & 2 & 4 \end{array}\right)\rightarrow \left(\begin{array}{ccc|c} 1 & -\frac{1}{4} & -\frac{1}{4} & 0 \\ 0 & 1 & \frac{7}{11} & \frac{40}{11} \\ 0 & 0 & 0 & 1 \end{array}\right)\rightarrow \left(\begin{array}{ccc|c} 1 & 0 & -\frac{1}{11} & 0 \\ 0 & 1 & \frac{7}{11} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$

Die dritte Zeile sorgt dafür, dass das Gleichungssystem keine Lösung besitzt. Die Ebenen müssen dementsprechend parallel zueinander liegen.

$\left(\begin{array}{ccc|c} 2 & -2 & -1 & 5 \\ 0 & 1 & 1 & 4 \\ 1 & -1 & 0 & 3 \end{array}\right)\rightarrow \left(\begin{array}{ccc|c} 1 & -1 & -\frac{1}{2} & \frac{5}{2} \\ 0 & 1 & 1 & 4 \\ 0 & 0 & 1 & 1 \end{array}\right)\rightarrow \left(\begin{array}{ccc|c} 1 & 0 & 0 & 6 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 1 \end{array}\right)$

Du erhälst eine eindeutige Lösung mit $x_1=6$ , $x_2=3$ und $x_3=1$ . Der Punkt $S\,(6\mid 3\mid 1)$ ist der Schnittpunkt der drei Ebenen.

Du sollst das Gleichungssystem in Matrixform lösen und das Ergebniss in einen geometrischen Zusammenhang setzen.

$\left(\begin{array}{ccc|c} 1 & -2 & 3 & -1 \\ 2 & 1 & -4 & 3 \\ 3 & 2 & -5 & 7 \end{array}\right)\rightarrow \left(\begin{array}{ccc|c} 1 & -2 & 3 & -1 \\ 0 & 1 & -2 & 1 \\ 0 & 0 & 1 & 1 \end{array}\right)\rightarrow \left(\begin{array}{ccc|c} 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 1 \end{array}\right)$

Du erhälst eine eindeutige Lösung mit $x_1=2$ , $x_2=3$ und $x_3=1$ . Der Punkt $S\,(2\mid 3\mid 1)$ ist der Schnittpunkt der drei Ebenen.

$\left(\begin{array}{ccc|c} 1 & 2 & 0 & 1 \\ 5 & 8 & 3 & 1 \\ 4 & 8 & 0 & 4 \end{array}\right)\rightarrow \left(\begin{array}{ccc|c} 1 & 2 & 0 & 1 \\ 0 & 1 & -\frac{3}{2} & 2 \\ 0 & 0 & 0 & 0 \end{array}\right)\rightarrow \left(\begin{array}{ccc|c} 1 & 0 & 3 & -3 \\ 0 & 1 & -\frac{3}{2} & 2 \\ 0 & 0 & 0 & 0 \end{array}\right)$

Im Gleichungssystem wird über die $x_3$ -Konstante keine Aussage getroffen, wähle somit $x_3=t$ . Für die anderen zwei Komponenten erhälst du $x_1=-3-3\cdot t$ und $x_2=2+\frac{3}{2}\cdot t$ . Als Vektor schreib es sich:

$\overrightarrow{x}=\pmatrix{-3-3\cdot t \\ 2+\frac{3}{2}\cdot t \\ t}=\pmatrix{-3\\2\\0}+t\cdot\pmatrix{-3\\ \frac{3}{2} \\ 1}$

Dies ist eine Geradengleichung, die drei Ebenen schneiden sich in dieser Geraden.

$\left(\begin{array}{ccc|c} 1 & 5 & 8 & 0 \\ 1 & 2 & 5 & 4 \\ 2 & 10 & 16 & 2 \end{array}\right)\rightarrow \left(\begin{array}{ccc|c} 1 & 5 & 8 & 0 \\ 0 & 1 & 1 & -\frac{4}{3} \\ 0 & 0 & 0 & 1 \end{array}\right)\rightarrow \left(\begin{array}{ccc|c} 1 & 0 & 3 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$

Die dritte Zeile sorgt dafür, dass das Gleichungssystem keine Lösung besitzt. Die Ebenen müssen dementsprechend parallel zueinander liegen.

$\left(\begin{array}{ccc|c} 3 & 8 & 16 & 2 \\ 3 & 5 & 7 & 5 \\ 1 & 1 & 1 & 4 \end{array}\right)\rightarrow \left(\begin{array}{ccc|c} 1 & \frac{8}{3} & \frac{16}{3} & \frac{2}{3} \\ 0 & 1 & 3 & -1 \\ 0 & 0 & 1 & \frac{5}{2} \end{array}\right)\rightarrow \left(\begin{array}{ccc|c} 1 & 0 & 0 & 10 \\ 0 & 1 & 0 & \frac{-17}{2} \\ 0 & 0 & 1 & \frac{5}{2} \end{array}\right)$

Du erhälst eine eindeutige Lösung mit $x_1=10$ , $x_2=-\frac{17}{2}$ und $x_3=\frac{5}{2}$ . Der Punkt $S\,(10\mid -\frac{17}{2}\mid \frac{5}{2})$ ist der Schnittpunkt der drei Ebenen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?