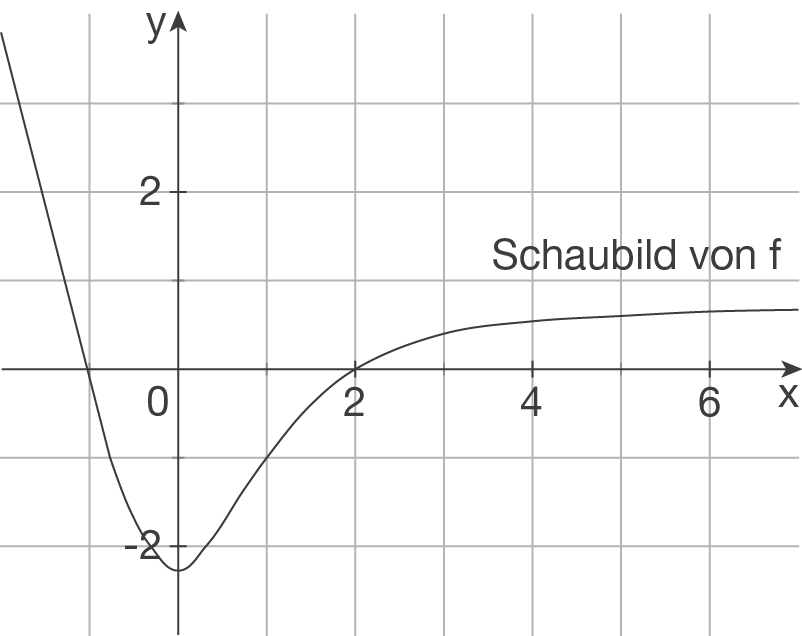
Funktion gegeben: Eigenschaften von Kurven
Sei 
eine gegebene Funktion und 
eine zu gehörende Stammfunktion. Dann kannst mit Hilfe der Funktion Eigenschaften von bestimmen:
Steigung
Die Steigung von in einer Stelle 
entspricht dem Funktionswert von an der Stelle .
Extremstellen/Sattelpunkte
Die Nullstellen von sind Extremstellen/Sattelpunkte der Funktion .
Wendepunkte
Hat an einer Stelle eine Extremstelle, so hat die Funktion an dieser Stelle einen Wendepunkt.
Monotonie
. Bestimme Eigenschaften der Stammfunktion von .
(strenge monoton, wenn
)
(streng monoton
).
Beispiel
Gegeben ist die Funktion- Extremstellen/Sattelpunkte:
- Nullstelle bei
einen Tiefpunkt (Vorzeichenwechsel von
nach
)
- Doppelte Nullstelle bei
(kein Vorzeichenwechsel)
- Nullstelle bei
- Wendepunkte:
- Tiefpunkt bei
einen Wendepunkt
- Hochpunkt bei
- Tiefpunkt bei
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
Begründen der Aussagen
a)
Wenn eine Stammfunktion von ist, heißt das, dass die Ableitung der Funktion ist.
besitzt überall dort Extremstellen, wo die Ableitung Nullstellen (mit Vorzeichenwechsel) besitzt, also an den Stellen und 
.
besitzt überall dort Wendestellen, wo die Ableitung Extremstellen hat. Dies ist an der Stelle der Fall.
Wenn
eine weitere Stammfunktion von ist, gilt allgemein 
(Unbestimmtheit der Stammfunktion). Für unsere Stammfunktion bedeutet das:
Wir können zwar Aussagen machen, an welchen Stellen die Stammfunktion Extremstellen bzw. Wendestellen hat, allerdings nicht über die
-Koordinaten dieser Punkte (der Wert 
verschiebt nämlich das Schaubild von beliebig in -Richtung). Über mögliche Nullstellen von lassen sich daher keine Aussagen treffen.
Wenn
Wir können zwar Aussagen machen, an welchen Stellen die Stammfunktion Extremstellen bzw. Wendestellen hat, allerdings nicht über die
b)
Die Differenz 
bezeichnet ein Integral über der Funktion . Es gilt nämlich:
.
Dieses Integral beschreibt den Inhalt der Fläche zwischen dem Graphen von und der -Achse und zwar im Bereich von bis 
. Wir können diesen Flächeninhalt durch Auszählen der Kästchen grob bestimmen, er umfasst etwa 2 Kästchen mit je 1 FE Flächeninhalt, insgesamt also etwa 2 FE.
Damit ist
und die Aussage ist begründet.
Dieses Integral beschreibt den Inhalt der Fläche zwischen dem Graphen von
Damit ist