Ganzrationale Funktionen
Ganzrationale Funktionen sind Polynomfunktionen, also Funktionen der Form:
 Wenn du die Kurve einer ganzrationalen Funktion gegeben hast, kannst du so vorgehen:
1. Schritt: Grad der Funktion bestimmen
Folgende Funktionsgraphen sind typisch für ganzrationale Funktionen:
2. Schritt: Funktionsgleichungen aufstellen
Durch ablesen von geeigneten Eigenschaften aus dem Schaubild, kannst du ein lineares Gleichungssystem aufstellen und dieses nach den unbekannten Parametern
Wenn du die Kurve einer ganzrationalen Funktion gegeben hast, kannst du so vorgehen:
1. Schritt: Grad der Funktion bestimmen
Folgende Funktionsgraphen sind typisch für ganzrationale Funktionen:
2. Schritt: Funktionsgleichungen aufstellen
Durch ablesen von geeigneten Eigenschaften aus dem Schaubild, kannst du ein lineares Gleichungssystem aufstellen und dieses nach den unbekannten Parametern  bis
bis  lösen.
Mögliche nützliche Eigenschaften sind:
Beachte, das du immer eine Gleichung mehr brauchst als der Grad der Funktion (zum Beispiel Funktion dritten Grades: 4 Gleichungen).
lösen.
Mögliche nützliche Eigenschaften sind:
Beachte, das du immer eine Gleichung mehr brauchst als der Grad der Funktion (zum Beispiel Funktion dritten Grades: 4 Gleichungen).
Funktionen 1. Grades (Gerade)

Funktionen 2. Grades (Parabel)

Funktionen 3. Grades

Funktionen 4. Grades 

- Achsensymmetrie
- Punktsymmetrie
- Extrempunkte
- Wendepunkte
- Gut ablesbare Koordinaten bestimmter Punkte
1.
Gegeben sind die Schaubilder einiger Funktionen. Bestimme einen möglichen Funktionsterm.

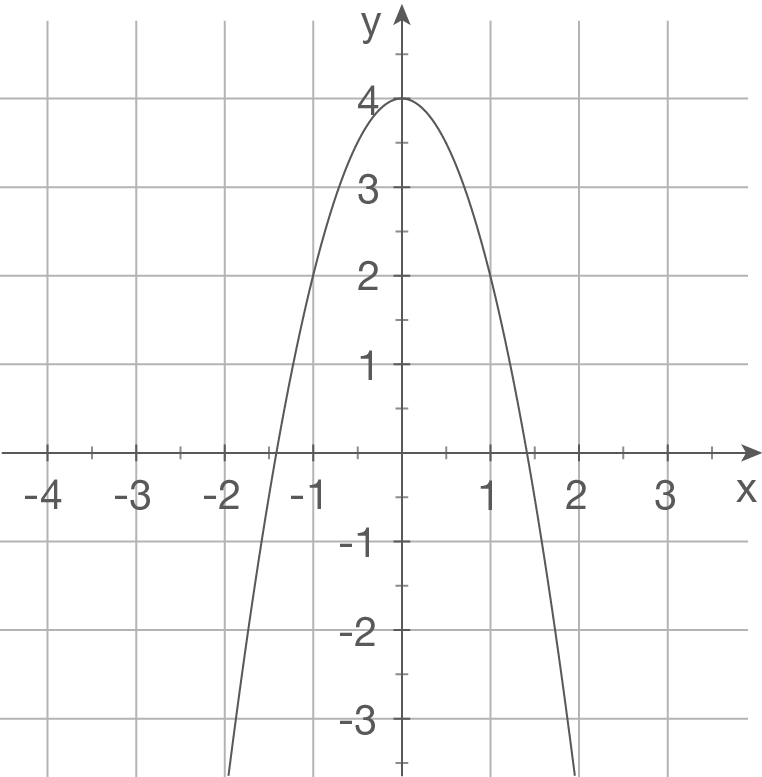
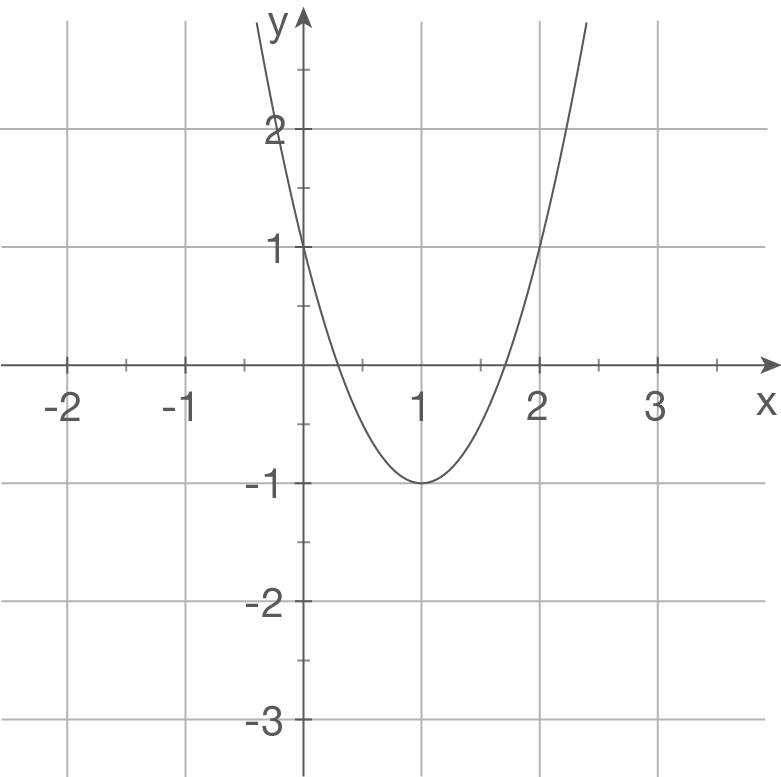
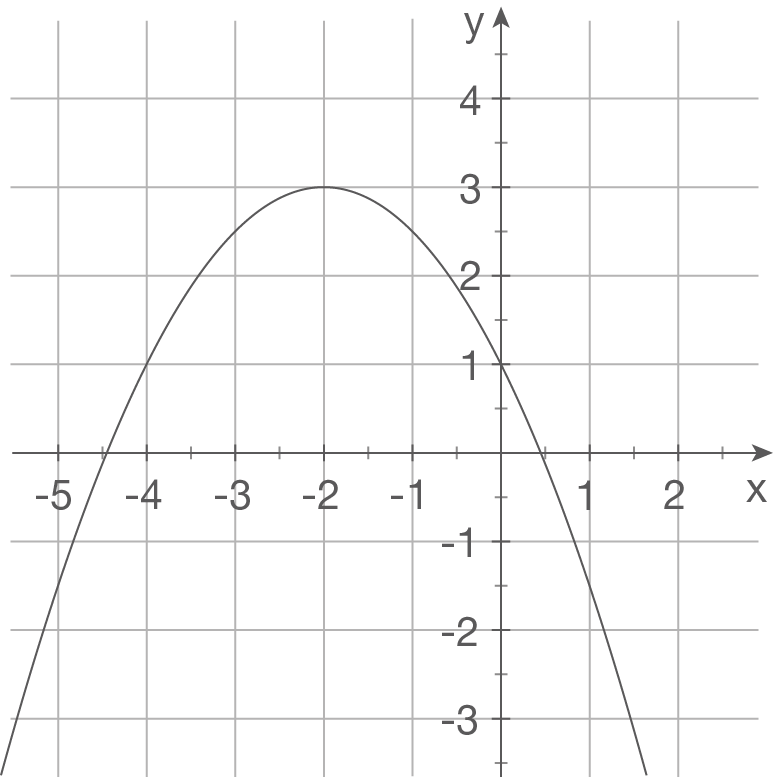
a)

b)

c)

d)

2.
Gegeben sind die Schaubilder einiger Funktionen. Bestimme einen möglichen Funktionsterm.
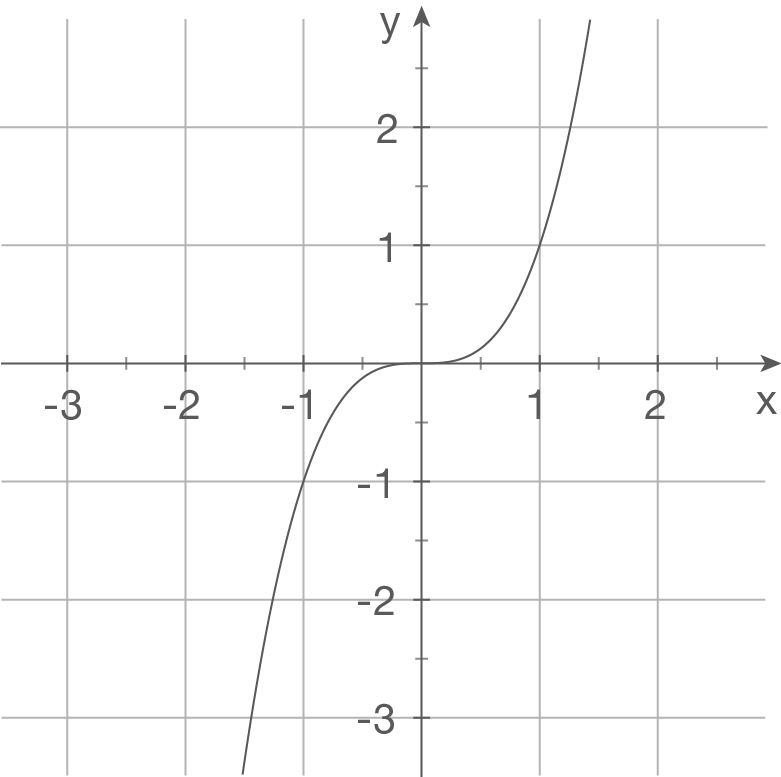

a)

b)

c)

d)

3.
Gegeben sind die Schaubilder einiger Funktionen. Bestimme einen möglichen Funktionsterm.

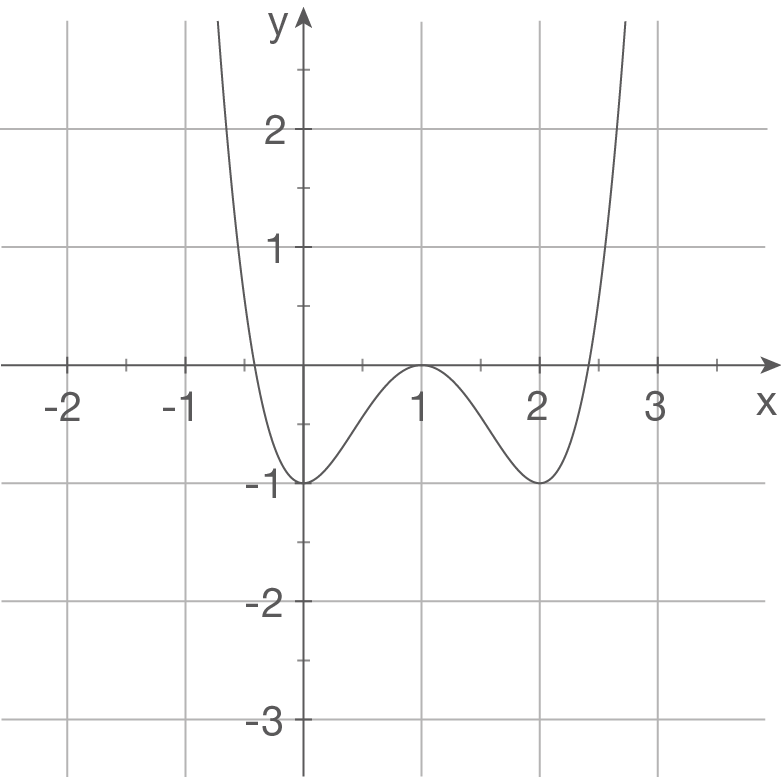
a)

b)

c)

d)

Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
Setze die Koordinaten von
Lies nun die Koordinaten eines weiteren Punktes ab, der auf dem Graphen liegt, z.B.
Lies aus der Abbildung die Koordinaten zweier Punkte ab, die auf dem Graphen liegen, z.B.
Einsetzen in
Die Funktionsgleichung lautet damit
b)
Lies nun die Koordinaten eines weiteren Punktes ab, der auf dem Graphen liegt, z.B.
Lies aus der Abbildung die Koordinaten zweier Punkte ab, die auf dem Graphen liegen, z.B.
Einsetzen in
Die Funktionsgleichung lautet damit
c)
Lies nun die Koordinaten eines weiteren Punktes ab, der auf dem Graphen liegt, z.B.
Lies aus der Abbildung die Koordinaten dreier Punkte ab, die auf dem Graphen liegen, z.B.
Einsetzen in
Einsetzen in (2) liefert:
Also ist
Es folgt damit die Funktionsgleichung
d)
Lies nun die Koordinaten eines weiteren Punktes ab, der auf dem Graphen liegt, z.B.
Lies aus der Abbildung die Koordinaten dreier Punkte ab, die auf dem Graphen liegen, z.B.
Einsetzen in
Es folgt damit die Funktionsgleichung
2.
a)
Die Abbildung zeigt den Graphen einer Funktion 3. Grades, die punktsymmetrisch zum Ursprung ist. Als allgemeine Funktionsgleichung folgt damit
 mit der ersten Ableitung
mit der ersten Ableitung
 .
.
Es sind zwei Unbekannte zu bestimmen. Du benötigst also zwei Bedingungen. Zum einen kannst du die Koordinaten von ablesen. Daraus folgt die Bedingung
ablesen. Daraus folgt die Bedingung  . Zum anderen besitzt der Graph im Ursprung einen Sattelpunkt:
. Zum anderen besitzt der Graph im Ursprung einen Sattelpunkt:  .
.
Aus den beiden Bedingungen folgt ein lineares Gleichungssystem:
 Setze
Setze  ein in (1) und erhalte:
ein in (1) und erhalte:

Damit folgt die Funktionsgleichung .
.
Es sind zwei Unbekannte zu bestimmen. Du benötigst also zwei Bedingungen. Zum einen kannst du die Koordinaten von
| Hinweis: | Da die Punktsymmetrie zum Ursprung bereits verwendet wurde, ist die Bedingung |
Damit folgt die Funktionsgleichung
b)
Die Abbildung zeigt den Graphen einer Funktion 3. Grades, die punktsymmetrisch zum Ursprung ist. Als allgemeine Funktionsgleichung folgt damit
 mit der ersten Ableitung
mit der ersten Ableitung
 .
.
Es sind zwei Unbekannte zu bestimmen. Du benötigst also zwei Bedingungen. Der Graph besitzt den Hochpunkt . Daraus folgen die Bedingungen
. Daraus folgen die Bedingungen  und
und  . Aus den beiden Bedingungen folgt ein lineares Gleichungssystem:
. Aus den beiden Bedingungen folgt ein lineares Gleichungssystem:
Aus (2) folgt . Setze dies ein in (1):
. Setze dies ein in (1):




Also ist . Damit folgt die Funktionsgleichung
. Damit folgt die Funktionsgleichung  .
.
Es sind zwei Unbekannte zu bestimmen. Du benötigst also zwei Bedingungen. Der Graph besitzt den Hochpunkt
Aus (2) folgt
Also ist
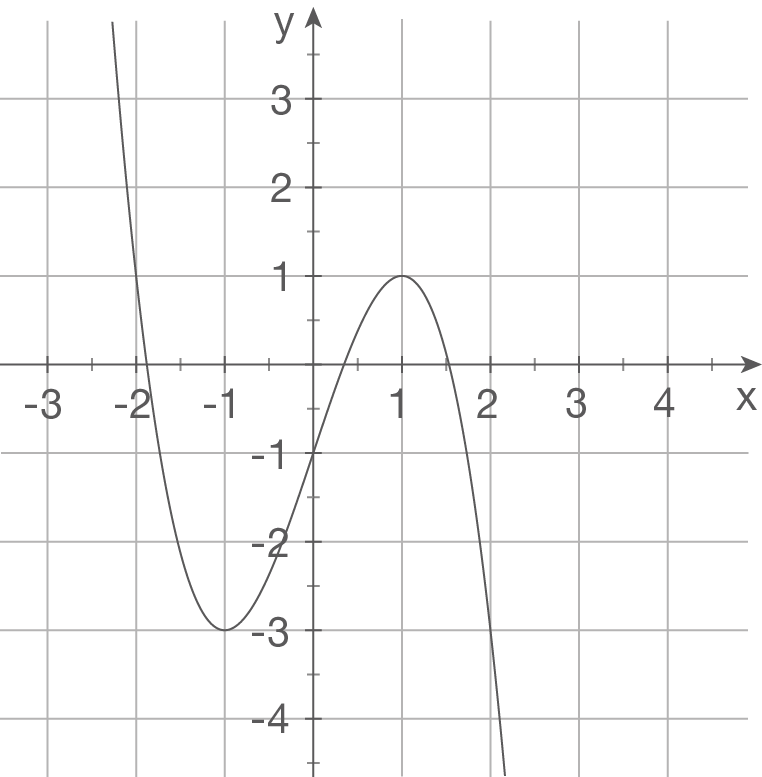
c)
Die Abbildung zeigt den Graphen einer Funktion 3. Grades. Als allgemeine Funktionsgleichung folgt damit
 mit der ersten Ableitung
mit der ersten Ableitung
 und der zweiten Ableitung
und der zweiten Ableitung
 .
.
Es sind vier Unbekannte zu bestimmen. Du benötigst also vier Bedingungen. Der Graph besitzt den Hochpunkt und den Wendepunkt
und den Wendepunkt  . Daraus folgen vier Bedingungen
. Daraus folgen vier Bedingungen

 und
und 


 und
und 
 Daraus ergibt sich ein lineares Gleichungssystem:
Daraus ergibt sich ein lineares Gleichungssystem:
Aus (2)a folgt .
.
Setze dies ein in (1):



Damit folgt die Funktionsgleichung .
.
Es sind vier Unbekannte zu bestimmen. Du benötigst also vier Bedingungen. Der Graph besitzt den Hochpunkt
Aus (2)a folgt
Setze dies ein in (1):
Damit folgt die Funktionsgleichung
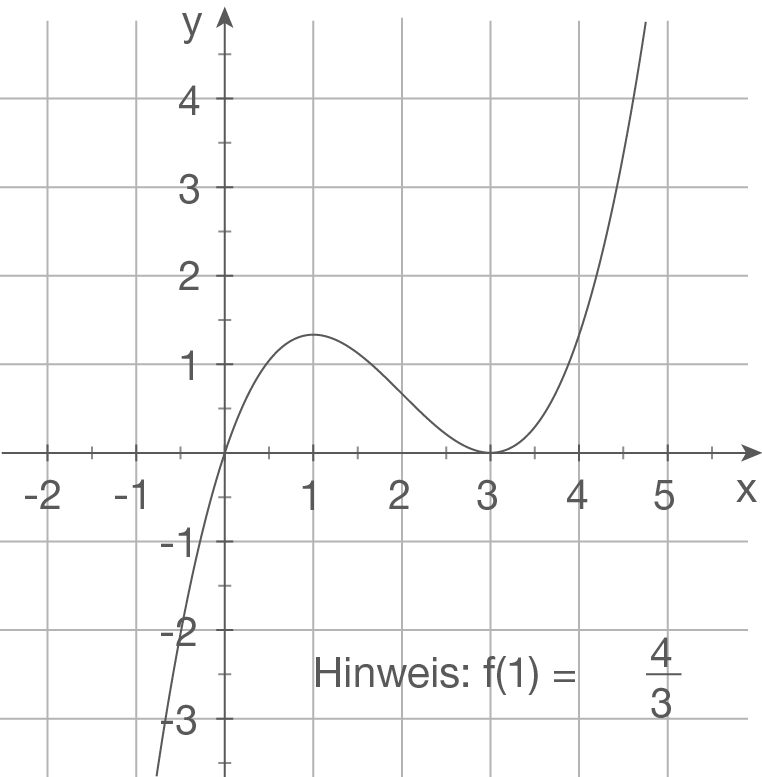
d)
Aus der Abbildung folgt sofort:
besitzt eine einfache Nullstelle bei
(Schnittpunkt mit der
-Achse)
besitzt eine doppelte Nullstelle bei
(Berührpunkt mit der
-Achse)
Lies nun einen weiteren Punkt ab, der auf dem Graphen liegt, z.B:
Die Funktionsgleichung lautet
Es sind vier Unbekannte zu bestimmen. Du benötigst also vier Bedingungen. Der Graph verläuft durch den Ursprung und durch den Punkt
und
und
Aus (4)b folgt:
Setze
Damit folgt die Funktionsgleichung
3.
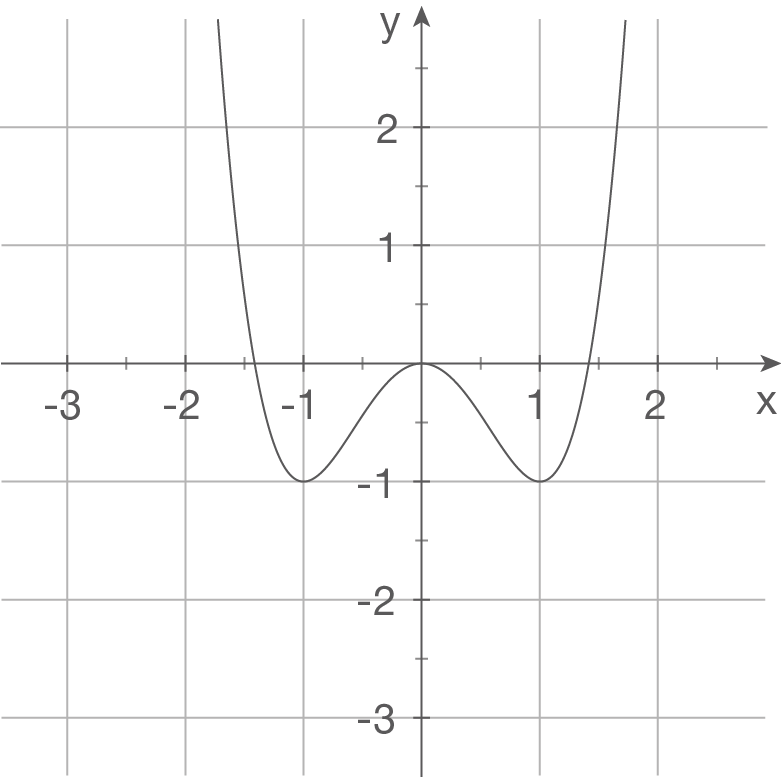
a)
Die Abbildung zeigt den Graphen einer Funktion 4. Grades, der achsensymmetrisch zur  -Achse ist. Als allgemeine Funktionsgleichung folgt damit
-Achse ist. Als allgemeine Funktionsgleichung folgt damit
 mit der ersten Ableitung
mit der ersten Ableitung
 .
.
Es sind drei Unbekannte zu bestimmen. Du benötigst also drei Bedingungen. Der Graph verläuft durch den Ursprung und besitzt den Tiefpunkt . Daraus folgen drei Bedingungen
. Daraus folgen drei Bedingungen
Aus (3) folgt:

 .
.
Setze dies ein in (2):

 .
.
Also ist .
.
Damit folgt die Funktionsgleichung .
.
Es sind drei Unbekannte zu bestimmen. Du benötigst also drei Bedingungen. Der Graph verläuft durch den Ursprung und besitzt den Tiefpunkt
und
Aus (3) folgt:
Setze dies ein in (2):
Also ist
Damit folgt die Funktionsgleichung
b)
Die Abbildung zeigt den Graphen einer Funktion 4. Grades, der achsensymmetrisch zur  -Achse ist. Als allgemeine Funktionsgleichung folgt damit
-Achse ist. Als allgemeine Funktionsgleichung folgt damit
 mit der ersten Ableitung
mit der ersten Ableitung
 .
.
Es sind drei Unbekannte zu bestimmen. Du benötigst also drei Bedingungen. Der Graph verläuft durch den Punkt und besitzt den Tiefpunkt
und besitzt den Tiefpunkt  . Daraus folgen drei Bedingungen
. Daraus folgen drei Bedingungen
Aus (3)a folgt:

 .
.
Setze dies ein in (2):


Damit folgt die Funktionsgleichung .
.
Es sind drei Unbekannte zu bestimmen. Du benötigst also drei Bedingungen. Der Graph verläuft durch den Punkt
und
Aus (3)a folgt:
Setze dies ein in (2):
Damit folgt die Funktionsgleichung
c)
Die Abbildung zeigt den Graphen einer Funktion 4. Grades, der achsensymmetrisch zur  -Achse ist. Als allgemeine Funktionsgleichung folgt damit
-Achse ist. Als allgemeine Funktionsgleichung folgt damit
 mit der ersten Ableitung
mit der ersten Ableitung
 .
.
Es sind drei Unbekannte zu bestimmen. Du benötigst also drei Bedingungen. Der Graph verläuft durch die Punkte und
und  und besitzt einen Hochpunkt bei
und besitzt einen Hochpunkt bei  . Daraus folgen drei Bedingungen
. Daraus folgen drei Bedingungen
Aus (3)a folgt:

 .
.
Setze dies ein in (1):


Damit folgt die Funktionsgleichung .
.
Es sind drei Unbekannte zu bestimmen. Du benötigst also drei Bedingungen. Der Graph verläuft durch die Punkte
Aus (3)a folgt:
Setze dies ein in (1):
Damit folgt die Funktionsgleichung
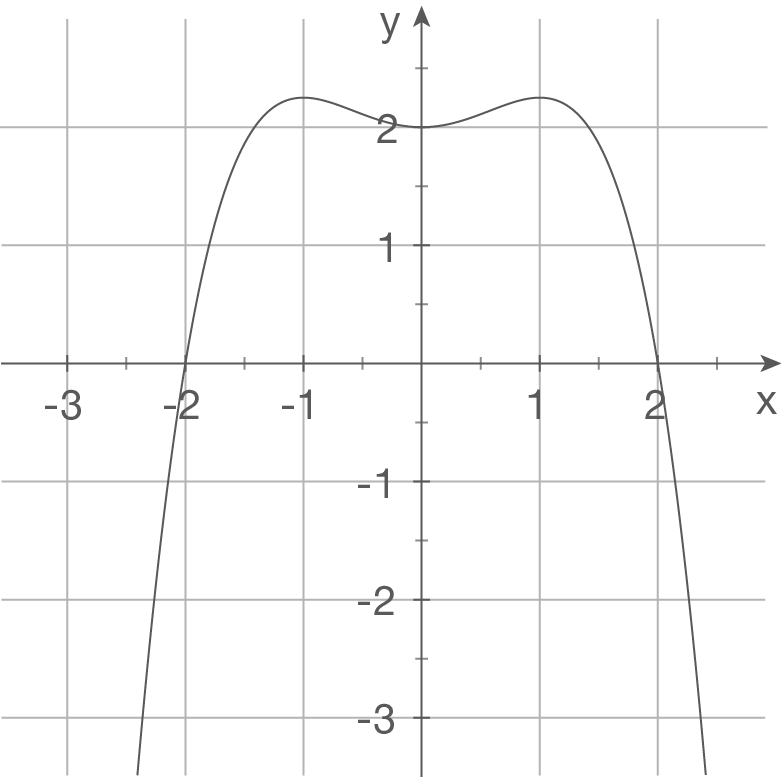
d)
Die Abbildung zeigt den Graphen einer Funktion 4. Grades. Als allgemeine Funktionsgleichung folgt damit
 mit der ersten Ableitung
mit der ersten Ableitung

Es sind fünf Unbekannte zu bestimmen. Du benötigst also fünf Bedingungen. Der Graph besitzt den Hochpunkt und die Tiefpunkte
und die Tiefpunkte  und
und  . Daraus folgen fünf Bedingungen
. Daraus folgen fünf Bedingungen
Aus (5)b folgt: .
.
Setze dies ein in (2)a:




Setze zuletzt und
und  ein in (1):
ein in (1):
 .
.
Damit folgt die Funktionsgleichung .
.
Es sind fünf Unbekannte zu bestimmen. Du benötigst also fünf Bedingungen. Der Graph besitzt den Hochpunkt
und
und
Aus (5)b folgt:
Setze dies ein in (2)a:
Setze zuletzt
Damit folgt die Funktionsgleichung