Vermischte Aufgaben
1.
Gegeben ist die Funktion 
mit 
, sowie der Punkt 
.
a)
Bestimme den minimalen Abstand von 
zum Graphen von .
b)
Zwischen der 
-Achse und dem Graphen von , also im ersten und zweiten Quadranten, soll ein Rechteck einbeschrieben werden. Zwei Eckpunkte liegen auf der -Achse, zwei auf dem Graphen der Funktion . Bestimme den maximalen Umfang dieses Rechtecks.
Betrachte nun dieses Rechteck mit maximalem Umfang: wie groß ist sein Flächeninhalt?
Betrachte nun dieses Rechteck mit maximalem Umfang: wie groß ist sein Flächeninhalt?
c)
Aus dem 
-fachen dieses Flächeninhalts soll ein Zylinder geformt werden. Die Fläche, die zur Verfügung steht, wird für die komplette Oberfläche benutzt.
Wie groß ist das maximale Volumen dieses Zylinders?
Wie groß ist das maximale Volumen dieses Zylinders?
2.
Gegeben ist die Funktion mit 
.
a)
Im ersten Quadranten soll zwischen der -Achse und dem Graphen von ein Rechteck einbeschrieben werden. Zwei Eckpunkte liegen auf der -Achse, einer auf dem Graphen der Funktion und ein vierter auf der 
-Achse.
Bestimme den maximalen Umfang dieses Rechtecks.
Bestimme den maximalen Umfang dieses Rechtecks.
b)
Ist das Rechteck mit dem größten Umfang gleichzeitig auch das mit dem größten Flächeninhalt?
c)
Ein Zylinder besitzt eine Oberfläche von 
. Wie groß ist sein maximales Volumen?
3.
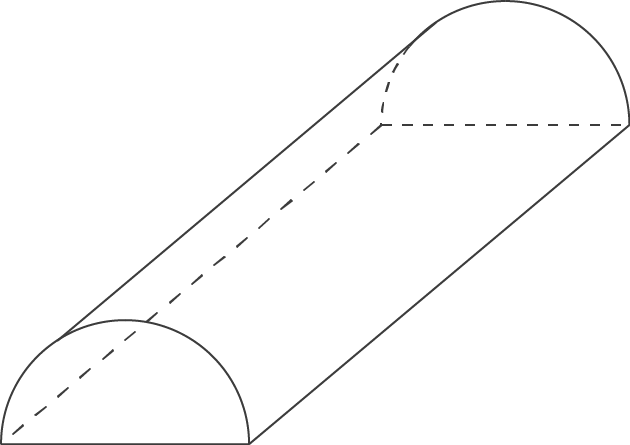
Die Figur unten stellt einen Schokoriegel dar. Aus Produktionsgründen soll die Verpackung nur 25cm
groß sein. Hinweis: Berechnung der Verpackung ohne Boden des Riegels.
Bestimme das maximale Volumen des Schokoriegels.
Bestimme das maximale Volumen des Schokoriegels.
4.
Eine Fastfoodkette verkauft einen Burger, der 90g Fleisch enthält und zum Preis von 0,98€ angeboten wird. Die Herstellungskosten eines Burgers belaufen sich auf etwa 0,40€. Am Tag wird dieser Burger etwa 40.000 Mal verkauft.
Ein Marktführer hat erkannt, dass der Burger mit mehr Fleisch saftiger aussieht und deshalb von den Kunden öfter verlangt wird. Pro Gramm Fleisch, das der Burger mehr enthält, werden am Tag 1000 Stück mehr verkauft.
Allerdings erhöht sich der Herstellungspreis pro Gramm Fleisch um 1 Cent pro Burger.
Wie viel Fleisch müsste der Burger enthalten, um der Fastfoodkette den maximalen Gewinn zu bescheren?
Wie groß ist dieser maximale Gewinn?
Ein Marktführer hat erkannt, dass der Burger mit mehr Fleisch saftiger aussieht und deshalb von den Kunden öfter verlangt wird. Pro Gramm Fleisch, das der Burger mehr enthält, werden am Tag 1000 Stück mehr verkauft.
Allerdings erhöht sich der Herstellungspreis pro Gramm Fleisch um 1 Cent pro Burger.
Wie viel Fleisch müsste der Burger enthalten, um der Fastfoodkette den maximalen Gewinn zu bescheren?
Wie groß ist dieser maximale Gewinn?
5.
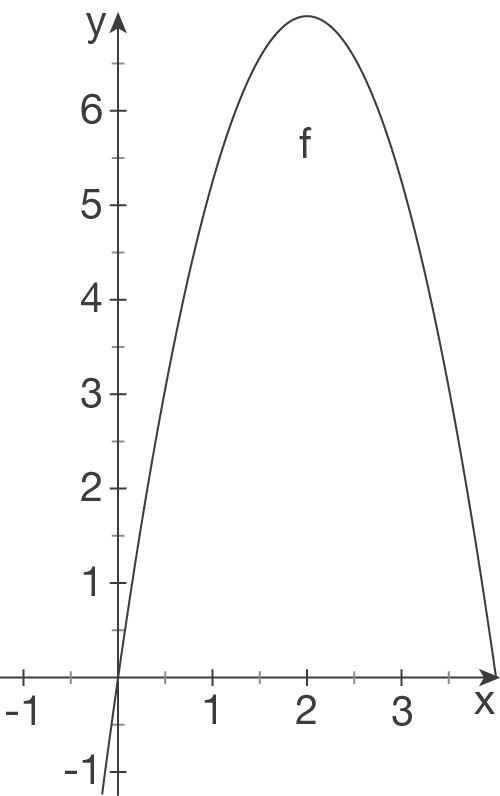
Auf einer Höhe will ein Bauer eine Weide für seine Kühe absperren. Das Schaubild unten zeigt das Gelände von oben.
Die-Achse bildet ein großer Gebirgsrücken, die Kurve bildet das Ende der Ebene; bis zur Kurve könne die Tiere weiden, dann geht es fast senkrecht den Berg hinab.
Damit seinen Tieren nichts passiert, möchte der Bauer das Gelände in einer rechteckigen Form absperren, auf der Seite, wo der Gebirgsrücken ist, möchte er allerdings keinen Zaun hin bauen.
Bestimme den maximalen Inhalt der Fläche und gib die jeweiligen Seitenlängen des Zauns an.
Die Kurve kann durch die Funktion mit 
beschrieben werden.
Die
Damit seinen Tieren nichts passiert, möchte der Bauer das Gelände in einer rechteckigen Form absperren, auf der Seite, wo der Gebirgsrücken ist, möchte er allerdings keinen Zaun hin bauen.
Bestimme den maximalen Inhalt der Fläche und gib die jeweiligen Seitenlängen des Zauns an.
Die Kurve kann durch die Funktion
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
Gegeben ist die Funktion , sowie der Punkt .
a)
Minimalen Abstand bestimmen
Wir haben nun also die Funktion bestimmt, die uns den Abstand vom zu jedem beliebigen Punkt auf angibt. Um den minimalen Abstand zu bestimmen, wird nun das Minimum dieser Abstandsfunktion bestimmt. Dies funktioniert mit Hilfe der ersten Ableitung.
Minimum bestimmen:
![\(\begin{array}[t]{rll}
d‘\left(u\right)=&0\\
2u^3-4=&0&\scriptsize{\mid\;+4}\\
2u^3&4&\scriptsize{\mid\;:2}\\
u^3=&2&\scriptsize{\mid\;\sqrt[3]{\;}}\\
u=&\sqrt[3]{2}
\end{array}\)](https://mathjax.schullv.de/c70ba390e6f36a223efccbd748c5a2d89333e0b1b2d7dad0d0988738060ab99e?color=5a5a5a)
Hinreichende Bedingung überprüfen
Da der erste Bruch 
und im zweiten Bruch ![\(\left(2\left(\sqrt[3]{2}\right)^3-4\right) = 0\)](https://mathjax.schullv.de/2c415a8a36d5869a92109e5c48f847e79f56600da1bd68ad3e26e8d43e71b177?color=5a5a5a)
folgt 
.
An der Stelle ![\(u=\sqrt[3]{2}\)](https://mathjax.schullv.de/989b10874f55f7c9520ca0103ecd73f89d273cbe09a5c7f60ba37487d0c629ba?color=5a5a5a)
besitzt die Abstandsfunktion also ein Minimum. Den Abstand selbst gibt der Funktionswert ![\(d\left(\sqrt[3]{2}\right)\)](https://mathjax.schullv.de/aa3f72c66e949ade460ab33c9ccbf900e30aad33867bc531dd6d278095b7a113?color=5a5a5a)
an:
Der minimale Abstand von zu 
beträgt 
LE.
Vollständige Lösung anzeigen
b)
Funktionsgleichung aufstellen
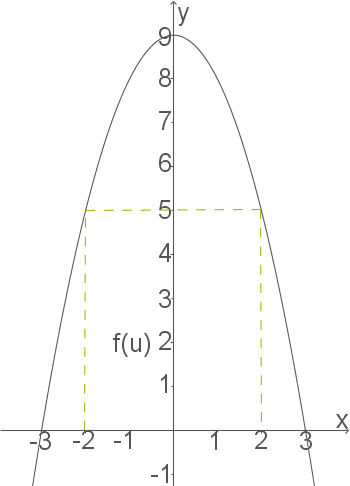
Zunächst muss eine Funktionsgleichung entwickelt werden, mit der wir den Umfang eines solchen Rechtecks berechnen können. Hierfür verdeutlichen wir uns die Aufgabe noch einmal mit Hilfe einer Skizze (das eingezeichnete Rechteck ist nicht das ideale, sondern ein beliebiges!):
Die Kantenlängen des Rechtecks haben also die Länge 
und 
.
Der Umfang berechnet sich immer dadurch, dass man die Längen aller Kanten addiert. In diesem Fall wäre der Umfang also:
Mit dieser Funktionsgleichung, die uns den Umfang in Abhängigkeit von 
angibt, können wir nun weiter rechnen und die Werte einsetzen:
![\(\begin{array}[t]{rll}
U\left(u\right)=&4u+2\left(9-u^2\right)\\[3pt]
=&4u+18-2u^2\\[3pt]
U\left(u\right)=&-2u^2+4u+18
\end{array}\)](https://mathjax.schullv.de/3b0366bea302c5ae06e81567fe0745deead416e4fed9e9df433c6d687c015756?color=5a5a5a)
Um den maximalen Umfang zu berechnen, wird nun die Maximalstelle dieser Funktion bestimmt:
![\(\begin{array}[t]{rll}
U\left(u\right)=&-2u^2+4u+18\\[3pt]
U‘\left(u\right)=&-4u+4\\[3pt]
U‘‘\left(u\right)=&-4
\end{array}\)](https://mathjax.schullv.de/2a8f52ad05b90515f2533b33c9e6f000e775eeaa1f1c9d8074ea14ed9a1f5334?color=5a5a5a)
Hochpunkt bestimmen:
![\(\begin{array}[t]{rll}
U‘\left(u\right)=&0\\[3pt]
-4u+4=&0&\scriptsize{\mid\;-4}\\[3pt]
-4u=&-4&\scriptsize{\mid\;:\left(-4\right)}\\[3pt]
u=&1
\end{array}\)](https://mathjax.schullv.de/c0e933fe8ad9e82d5f8302925fc11bd548898edb968578de2461eb158b0c7414?color=5a5a5a)
Überprüfen der hinreichenden Bedingung
![\(\begin{array}[t]{rll}
f‘‘\left(1\right)=&-4&\scriptsize{\lt 0:\,\text{Maximum}}
\end{array}\)](https://mathjax.schullv.de/3de463d1389248e488148fa1f7b255598e7b62f998b4ba3c24f913e91c6625a2?color=5a5a5a)
Für 
wird der Umfang des Rechtecks also maximal. Den Umfang selbst liefert uns die Umfangfunktion:
![\(\begin{array}[t]{rll}
U\left(1\right)=&-2\cdot1^2+4\cdot1+18\\
=&-2+4+18\\
U\left(1\right)=&20
\end{array}\)](https://mathjax.schullv.de/f94c2fc196188c04a32c39e00621c0aac0b485d179e8fcd942f554a0dade92dc?color=5a5a5a)
Der maximale Umfang des Rechtecks beträgt 
LE.
Es soll außerdem der Flächeninhalt dieses Rechtecks bestimmt werden, also für . Die Seiten des Rechtecks sind zum einen lang, um anderen 
. Für den Flächeninhalt des Rechtecks gilt mit also:
Das Rechteck mit maximalem Umfang hat den Flächeninhalt 
FE.
Der Umfang berechnet sich immer dadurch, dass man die Längen aller Kanten addiert. In diesem Fall wäre der Umfang also:
c)
Zunächst wollen wir uns den Lösungsweg an sich anschauen:
-fachen Flächeninhalt des Rechtecks aus b) einnehmen. Mit FE folgt für die Oberfläche des Zylinders: 
.
Beziehung zwischen 
und 
herstellen
in Volumenformel einsetzen
Hochpunkt bestimmen:
Hinreichende Bedingung überprüfen
Für 
wird das Volumen maximal.
Höhe eindeutig bestimmen
![\(\begin{array}[t]{rll}
\dfrac{24}{r}-r&=h&\scriptsize{\mid\;r=\sqrt{8}\, \text{einsetzen}}\\[3pt]
\dfrac{24}{\sqrt{8}}-\sqrt{8}&=h
\end{array}\)](https://mathjax.schullv.de/3e139abebfe5ea0a6005b439b3030e95fd6a98d9a1eefa3a26f027aaac892521?color=5a5a5a)
Volumen bestimmen
Das maximale Volumen des Zylinders beträgt 
.
- Über die Oberfläche können wir eine Beziehung zwischen
und
herstellen.
- Diese neue Gleichung lösen wir nach
- Der Wert für
- Es ergibt sich eine Gleichung für
, die nur von
- Der Hochpunkt dieser Gleichung wird bestimmt, er gibt uns das
2.
Gegeben ist die Funktion 
a)
Zunächst muss eine Funktionsgleichung entwickelt werden, mit der wir den Umfang eines solchen Rechtecks berechnen können. Hierfür verdeutlichen wir uns die Aufgabe noch einmal mit Hilfe einer Skizze (das eingezeichnete Rechteck ist nicht das ideale, sondern ein beliebiges!):
Die Kantenlängen des Rechtecks haben also die Länge und .
Der Umfang berechnet sich immer dadurch, dass man die Längen aller Kanten zusammenzählt. In diesem Fall wäre der Umfang also:
Mit dieser Funktionsgleichung, die uns den Umfang in Abhängigkeit von angibt, können wir nun weiter rechnen und die Werte einsetzen:
![\(\begin{array}[t]{rll}
U\left(u\right)&=2u+2\left(-u^3+8\right)\\[3pt]
&=2u-2u^3+16\\[3pt]
U\left(u\right)&=-2u^3+2u+16
\end{array}\)](https://mathjax.schullv.de/f5674262226f534f23d6a1fd0f2fcf1c8922379a19d4dacd401c383dbf5c72d9?color=5a5a5a)
Um den maximalen Umfang zu berechnen, wird nun der Hochpunkt dieser Umfangsfunktion bestimmt:
![\(\begin{array}[t]{rll}
U\left(u\right)&=-2u^3+2u+16\\[3pt]
U‘\left(u\right)&=-6u^2+2\\[3pt]
U‘‘\left(u\right)&=-12u
\end{array}\)](https://mathjax.schullv.de/28297fd53691c763f4c3c55d45c5c31db46941f1627beb95690a6987520ba5c1?color=5a5a5a)
Hochpunkt bestimmen:
![\(\begin{array}[t]{rll}
U‘\left(u\right)&=0\\[3pt]
-6u^2+2&=0&\scriptsize{\mid\;-2}\\[3pt]
-6u^2&=-2&\scriptsize{\mid\;:\left(-6\right)}\\[3pt]
u^2&=\dfrac{1}{3}&\scriptsize{\mid\;\sqrt{\;}}\\[3pt]
u_{1,2}&=\pm\sqrt{\dfrac{1}{3}}
\end{array}\)](https://mathjax.schullv.de/d00d047c53aca9ed7b3cd8f53096343b2ae3c2a12a329914036066cf724c1941?color=5a5a5a)
Hinreichende Bedingung überprüfen
Für 
wird der Umfang des Rechtecks also maximal. Den Umfang selbst liefert uns die Umfangfunktion:
Der maximale Umfang des Rechtecks beträgt 
LE.
Der Umfang berechnet sich immer dadurch, dass man die Längen aller Kanten zusammenzählt. In diesem Fall wäre der Umfang also:
b)
Als Skizze für diesen Aufgabenteil kann wieder die aus a) verwendet werden. Der allgemeine Flächeninhalt eines Rechtecks ist in diesem Falle:
Diese Funktion können wir ableiten. Dann setzen wir den Wert für aus 
ein. Ist 
, so handelt es sich um ein Extremum. Wenn nicht, so gibt es zwei Rechtecke, eines mit maximalem Umfang und ein anderes mit maximalem Flächeninhalt.
![\(\begin{array}[t]{rll}
A\left(u\right)&=u\cdot\left(8-u^3\right)\\[3pt]
&=8u-u^4\\[3pt]
A‘\left(u\right)&=8-4u^3\\[3pt]
A‘‘\left(u\right)&=-12u^2
\end{array}\)](https://mathjax.schullv.de/6ab8a55312945ae77cdca6a8266a99a0f54d17ce6fdb7d23b9d6df6dd3dc3470?color=5a5a5a)
in 
einsetzen:
Das Rechteck mit dem maximalen Umfang ist also nicht das Rechteck mit dem maximalen Flächeninhalt.
c)
Zunächst wollen wir uns den Lösungsweg an sich anschauen:
und herstellen
in Volumenformel einsetzen
Hochpunkt bestimmen:
Hinreichende Bedingung überprüfen
Für 
wird das Volumen maximal.
Höhe eindeutig bestimmen
![\(\begin{array}[t]{rll}
\dfrac{45}{r}-r&=h&\scriptsize{\mid\;r=\sqrt{15} \text{einsetzen}}\\[5pt]
\dfrac{45}{\sqrt{15}}-\sqrt{15}&=h
\end{array}\)](https://mathjax.schullv.de/e78a6ea6ed0f4c23143200b4ce70aaeefbd55829ae2ec89d4b0fd854bee3f177?color=5a5a5a)
Volumen bestimmen
Das maximale Volumen des Zylinders beträgt 
.
- Über die Oberfläche können wir eine Beziehung zwischen
- Diese neue Gleichung lösen wir nach
- Der Wert für
- Es ergibt sich eine Gleichung für
- Der Hochpunkt dieser Gleichung wird bestimmt, er gibt uns das
3.
Wir haben die Oberfläche des Schokoriegels fest gegeben, nämlich 25cm.
Sehen wir uns die Figur zunächst genauer an. Wir erkennen, dass es sich um einen „halben“ Zylinder handelt und dass seine Oberfläche aus verschiedenen Teilen besteht:![\(\begin{array}[t]{rll}
A_{\text{Kreis}}&=2\cdot\dfrac{1}{2}\pi\cdot r^2\\[5pt]
&=\pi\cdot r^2
\end{array}\)](https://mathjax.schullv.de/5cae16e97cb36d82bde7803f77f143389107195cc07ff1c3628e9c72d116a73b?color=5a5a5a)
Flächeninhalt der Mantelfläche
![\(\begin{array}[t]{rll}
A_{\text{Mantel}}&=h\cdot\dfrac{1}{2}\cdot2\cdot\pi\cdot r\\[5pt]
&=\pi\cdot r\cdot h
\end{array}\)](https://mathjax.schullv.de/1da1dcd1ee6a355334a97b87da90b39a75c52f1f98d049ded31ba722ea1ace54?color=5a5a5a)
Daraus ergibt sich die Oberflächenformel:
![\(\begin{array}[t]{rll}
A_{\text{gesamt}}&=A_{\text{Kreis}}+A_{\text{Mantel}}\\[3pt]
&=\pi\cdot r^2+\pi\cdot r\cdot h
\end{array}\)](https://mathjax.schullv.de/3e1b39b5b22e309ded2e6903b6244355f6944300c793fbcb25214fbb63de5dc6?color=5a5a5a)
Für 
können wir den Wert einsetzen, der uns in der Aufgabenstellung gegeben wurde, nämlich 
.
Die Gleichung lösen wir nun nach auf.
Wir sollen das maximale Volumen bestimmen. Die Volumenformel für den Zylinder lautet
Die Grundfläche ist ein Halbkreis, daher lautet die Gleichung
Für die Höhe setzen wir den Wert ein, den wir eben bestimmt haben. Damit erhalten wir eine Gleichung, die nur von abhängig ist.
Maximales Volumen bestimmen
bestimmen
![\(\begin{array}[t]{rll}
V&=\dfrac{1}{2}\cdot\pi\cdot r^2\cdot\left(\dfrac{25}{\pi\cdot r}-r\right)\\[5pt]
&=\dfrac{25\cdot\pi\cdot r^2}{2\cdot\pi\cdot r}-\dfrac{1}{2}\cdot\pi \cdot r^3\\[5pt]
&=\dfrac{25r}{2}-\dfrac{1}{2}\pi r^3
\end{array}\)](https://mathjax.schullv.de/5ed6d43c4bee2f135ebc3e96360ff086f120993be150c41452fbfd8150b28aa1?color=5a5a5a)
Diese Gleichung wird nun abgeleitet und dann gleich 0 gesetzt. Somit rechnen wir den Hochpunkt aus und bekommen damit den Wert für , bei dem das Volumen maximal wird.
Hochpunkt bestimmen:
![\(\begin{array}[t]{rll}
V\left(r\right)&=\dfrac{25r}{2}-\dfrac{1}{2}\pi r^3\\[5pt]
V‘\left(r\right)&=\dfrac{25}{2}-\dfrac{1}{2}\pi\cdot3r^2\\[5pt]
&=\dfrac{25}{2}-\dfrac{3}{2}\pi r^2\\[5pt]
V‘‘\left(r\right)&=-3\pi r
\end{array}\)](https://mathjax.schullv.de/77e30b76bd199f9220e09883b2221d9b08a419861e654fe1e60a45358255e5cf?color=5a5a5a)
setzen
![\(\begin{array}[t]{rll}
\dfrac{25}{2}-\dfrac{3}{2}\pi r^2&=0&\scriptsize{\mid\;+\dfrac{3}{2}\pi r^2}\\[5pt]
\dfrac{25}{2}&=\dfrac{3}{2}\pi r^2&\scriptsize{\mid\;:\pi}\\[5pt]
\dfrac{25}{2\pi}&=\dfrac{3}{2}r^2&\scriptsize{\mid\;\cdot\dfrac{2}{3}}\\[5pt]
\dfrac{25}{3\pi}&=r^2&\scriptsize{\mid\;\sqrt{\;}}\\[5pt]
\pm\dfrac{5}{\sqrt{3\pi}}&=r_{1,2}
\end{array}\)](https://mathjax.schullv.de/0aeae48b96e0981df505f007568ed9e4b324943569e1f2b23076a859fa9830d1?color=5a5a5a)
Da für den Radius nur positive Werte in Frage kommen, rechnen wir mit Lösung 
weiter.
Diesen Wert für setzen wir nun in die Volumengleichung ein und bestimmen das maximale Volumen.
Maximales Volumen bestimmen
Das maximale Volumen beträgt 
.
Sehen wir uns die Figur zunächst genauer an. Wir erkennen, dass es sich um einen „halben“ Zylinder handelt und dass seine Oberfläche aus verschiedenen Teilen besteht:
- Zwei gleich große Halbkreise
- Die Mantelfläche, die als Rechteck aufgefasst werden kann, mit den Seitenrändern
, dem halben Umfang des Kreises.
Die Gleichung lösen wir nun nach
4.
Halten wir zunächst fest, was wir wissen. Der Gewinn der Fastfoodkette lässt sich auffassen als der der Gewinn pro Burger multipliziert mit der Anzahl der verkauften Burger. Bei 
Fleisch pro Burger, wird dieser 
Mal verkauft. Wir können also schreiben:
Der Gewinn pro Burger wiederum setzt sich zusammen aus dem Verkaufspreis und den Herstellungskosten:
Der Verkaufspreis bleibt immer gleich, nämlich 0,98 € pro Burger.
Die Herstellungskosten allerdings erhöhen sich um 0,01 € pro zusätzlichem Gramm Fleisch.
Wenn wir also diese zusätzliche Fleischmenge als betrachten, können wir für die Herstellungskosten des Burgers schreiben:
Auch die Anzahl der Burger ist abhängig von dieser Fleischmenge. Pro zusätzlichem Gramm Fleisch, erhöht sich die Anzahl der verkauften Burger um 1000 Stück. Wir können also festhalten:
Wenn wir diese Teilgleichungen nun alle in der oberen Gleichung zusammenfassen, erhalten wir folgende Gleichung:
Diese Gleichung können wir nun vereinfachen:
Nun bestimmen wir den Hochpunkt dieser Funktion und erhalten das , für das der Gewinn maximal wird (Erinnerung: ist die zusätzliche Fleischmenge in Gramm.)
![\(\begin{array}[t]{rll}
G_{\text{gesamt}}\left(x\right)&=-10x^2+180x+23200\\[3pt]
G_{\text{gesamt}}‘\left(x\right)&=-10\cdot2x+180\\[3pt]
&=-20x+180\\[3pt]
G_{\text{gesamt}}‘‘\left(x\right)&=-20
\end{array}\)](https://mathjax.schullv.de/dae2456ecad78a8523ddcad4bc3bbcb3cc1d24f7f8be40dd66d0a85ec76ad71c?color=5a5a5a)
Hochpunkt bestimmen:
![\(\begin{array}[t]{rll}
G_{\text{gesamt}}‘\left(x\right)&=0\\[3pt]
-20x+180&=0&\scriptsize{\mid\;+20x}\\[3pt]
180&=20x&\scriptsize{\mid\;:20}\\[3pt]
9&=x
\end{array}\)](https://mathjax.schullv.de/428b4e0766059f3056c4b13fbbd262790672b0766f8a843bbdfc499b21277521?color=5a5a5a)
Hinreichende Bedingung überprüfen
![\(\begin{array}[t]{rll}
G_{\text{gesamt}}‘‘\left(9\right)&=-20&\scriptsize{\lt 0: \text{Hochpunkt}}
\end{array}\)](https://mathjax.schullv.de/d1630373d38801399fc06c5613e619421b58f946652a06d8b6689a6ba5385256?color=5a5a5a)
Die Fastfoodkette macht den größten Gewinn, wenn sie die Fleischmenge des Burgers um 9g erhöht.
Den Gewinn selbst bestimmen wir mit der Gleichung von oben:
Die Fastfoodkette macht bei einer zusätzlichen Fleischmenge von 9g pro Burger am Tag insgesamt 24010 € Gewinn.
5.
Wie wir sehen, müssen wir hier den maximalen Flächeninhalt bestimmen und zwar innerhalb einer Fläche, die von -Achse und einer Kurve eingeschlossen wird.
Um überhaupt etwas über die Größe dieser Fläche aussagen zu können, bestimmen wir zunächst die Nullstellen der Kurve, um eine klare Abgrenzung zu erhalten. Funktionsgleichung für Flächeninhalt bestimmen Nullstellen von ausrechnen
![\(\begin{array}[t]{rll}
-\dfrac{7}{4}x^2+7x&=0&\scriptsize{\mid\;\text{x ausklammern}}\\[5pt]
x\left(-\dfrac{7}{4}x+7\right)&=0
\end{array}\)](https://mathjax.schullv.de/3ea1b7e64a61dc01bb8d66aa43021a319c1059ed9d82ab672cc687e59440d82c?color=5a5a5a)
Ein Produkt ist 0, wenn einer seiner Faktoren 0 ist:
![\(\begin{array}[t]{rll}
x_1&=0\\[5pt]
-\dfrac{7}{4}x+7&=0&\scriptsize{\mid\;+\dfrac{7}{4}x}\\[5pt]
7&=\dfrac{7}{4}x&\scriptsize{\mid\;\cdot\dfrac{4}{7}}\\[5pt]
4&=x_2
\end{array}\)](https://mathjax.schullv.de/65ee61001a46ec7bc733735a686232f55820379100014f0888978d0ae4a7e4c2?color=5a5a5a)
Daraus ergeben sich die Punkte 
und 
.
Nun sehen wir uns die Fläche genauer an. Wir sollen ein Rechteck mit maximalem Flächeninhalt bestimmen.
Wenn wir die Differenz der-Werte der Nullstellen bilden, wissen wir, wie breit dieses Rechteck überhaupt werden kann:
Differenz der -Werte von 
und 
bestimmen
![\(\begin{array}[t]{rll}
4-0&=4
\end{array}\)](https://mathjax.schullv.de/65d05361c84c83693d022f069785be287cf6aa34cfadad8796c3fdf5eb8d8585?color=5a5a5a)
Das Rechteck kann also maximal 4 LE breit werden.
Die Teile der Strecke, die nicht berücksichtigt werden, können wir mit bezeichnen.
Dies wird in folgender Skizze anschaulich dargestellt:
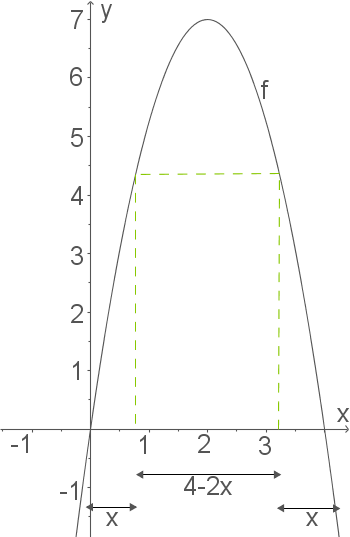Die Breite der Fläche beträgt also 
LE.
Die Höhe der Fläche ist auch recht leicht zu bestimmen, da die Eckpunkte auf der Kurve liegen müssen. Die Höhe ist also einfach der Funktionswert von , d.h. 
.
Die Formel für den Flächeninhalt von Rechtecken lautet
.
In unserem Fall wäre das also:
![\(\begin{array}[t]{rll}
A&=\left(4-2x\right)\cdot f\left(x\right)\\[5pt]
&=\left(4-2x\right)\cdot\left(-\dfrac{7}{4}x^2+7x\right)\\[5pt]
&=-7x^2+28x+\dfrac{7}{2}x^3-14x^2\\[5pt]
A&=\dfrac{7}{2}x^3-21x^2+28x
\end{array}\)](https://mathjax.schullv.de/bde18ed99b499235f0a7d2ff193c535de369ca9cf39cc5e4f3c237220587c2b2?color=5a5a5a)
Wir werden nun den Extremwert dieser Gleichung bestimmen und somit den Wert für erhalten, an dem der Flächeninhalt 
maximal wird.
Maximalen Flächeninhalt bestimmen
Ableitungen bilden
![\(\begin{array}[t]{rll}
A&=\dfrac{7}{2}x^3-21x^2+28x\\[5pt]
A‘&=\dfrac{7}{2}\cdot3x^2-21\cdot2x+28\\[5pt]
&=\dfrac{21}{2}x^2-42x+28\\[5pt]
A‘‘&=\dfrac{21}{2}\cdot2x-42\\[5pt]
&=21x-42
\end{array}\)](https://mathjax.schullv.de/e09858a996c2379b024e2da1eca311e5af50d80210c3a6e7bee49e6cc053caf6?color=5a5a5a)
setzen
![\(\begin{array}[t]{rll}
\dfrac{21}{2}x^2-42x+28&=0&\scriptsize{\mid\;\cdot\dfrac{2}{21}}\\[5pt]
x^2-\dfrac{84}{21}x+\dfrac{56}{21}&=0\\[5pt]
x^2-4x+\dfrac{56}{21}&=0
\end{array}\)](https://mathjax.schullv.de/8177f627470aff6ff2d85c325f1c0b71df589cfa801c73ec88a0f087372ef0fb?color=5a5a5a)
p-q-Formel anwenden
![\(\begin{array}[t]{rll}
x_{1,2}&=\dfrac{4}{2}\pm\sqrt{\left(\dfrac{4}{2}\right)^2-\dfrac{56}{21}}\\[5pt]
&=2\pm\sqrt{4-\dfrac{56}{21}}\\[5pt]
&=2\pm\sqrt{\dfrac{84}{21}-\dfrac{56}{21}}\\[5pt]
&=2\pm\sqrt{\dfrac{28}{21}}\\[5pt]
&=2\pm\sqrt{\dfrac{4}{3}}\\[5pt]
&=2\pm\dfrac{2}{\sqrt{3}}\\[5pt]
x_1 &\approx 3,1547\\[5pt]
x_2 &\approx 0,845
\end{array}\)](https://mathjax.schullv.de/fd87622b11cd2787323f026439d56f6e818b92e6439b8da9479cbf1199748826?color=5a5a5a)
Hinreichende Bedingung für 
prüfen
![\(\begin{array}[t]{rll}
A‘‘\left(3,1547\right)&=21\cdot\left(3,1547\right)-42\\[3pt]
&=66,2487-42\\[3pt]
&=24,2487 \;\scriptsize{ >0: \text{Tiefpunkt}}
\end{array}\)](https://mathjax.schullv.de/1c0f0e87fb14eedf4b219b120ad64bc0c437955e40084e9d36eabeff51aba57f?color=5a5a5a)
Hinreichende Bedingung für 
prüfen
![\(\begin{array}[t]{rll}
A‘‘\left(0,845\right)&=21\cdot0,845-42\\[3pt]
&=17,745-42\\[3pt]
&=-24,255 \;\scriptsize{\lt 0: \text{Hochpunkt}}
\end{array}\)](https://mathjax.schullv.de/ee11f7c372e9969feff48d9255ebe71f0adc3daa90f139b75ef5e53df97ef494?color=5a5a5a)
Für 
wird der Flächeninhalt maximal. Den Flächeninhalt selbst können wir mit der Gleichung von oben bestimmen.
Flächeninhalt bestimmen
Der maximale Flächeninhalt beträgt etwa 
FE.
Um überhaupt etwas über die Größe dieser Fläche aussagen zu können, bestimmen wir zunächst die Nullstellen der Kurve, um eine klare Abgrenzung zu erhalten. Funktionsgleichung für Flächeninhalt bestimmen Nullstellen von
Wenn wir die Differenz der
Die Teile der Strecke, die nicht berücksichtigt werden, können wir mit
Dies wird in folgender Skizze anschaulich dargestellt: