Normalenform

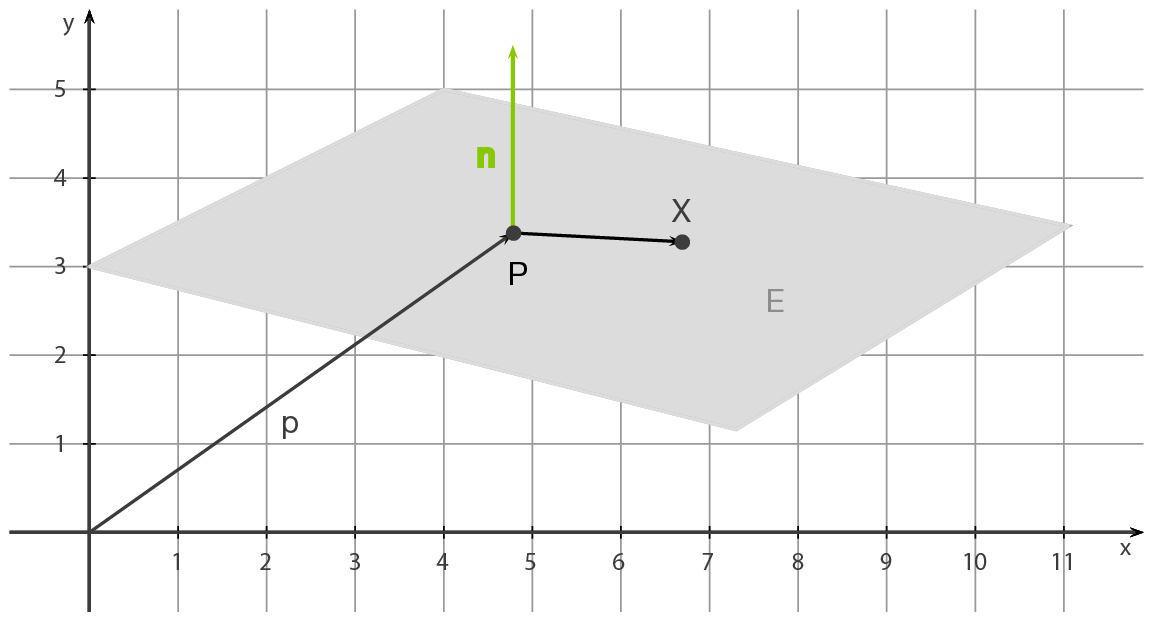
Eine Ebene im dreidimensionalen Raum kann durch einen Punkt und einen Normalenvektor, also einen Vektor, der senkrecht auf der Ebene steht, vollständig definiert werden:
Ist der Stützpunkt $P(p_1 \mid p_2 \mid p_3)$ und der Normalenvektor $\overrightarrow{n}$ gegeben, so kann die Gleichung einer Ebene $E$ in Normalenform wie folgt angegeben werden:

$E: \left( \overrightarrow{x} - \overrightarrow{p} \right)\circ\overrightarrow{n}=0$

Grafik eines 3D-Koordinatensystems mit einer Ebene und Vektoren.

Hast du anstelle des Normalenvektors $\overrightarrow{n}$ zwei Spannvektoren $\overrightarrow{u}$ und $\overrightarrow{v}$ der Ebene gegeben, so gibt es zwei Möglichkeiten, den Normalenvektor zu bestimmen:

Skalarprodukt:

Löse die Gleichungen $\overrightarrow{n} \circ \overrightarrow{u} = 0$ und $\overrightarrow{n} \circ \overrightarrow{v} = 0$ ,

Kreuzprodukt:

Berechne $\overrightarrow{n}$ = $\overrightarrow{u} \times \overrightarrow{v}$ .

Beispiel

Gegeben ist der Punkt $P(1 \mid 1 \mid 7)$ und der Normalenvektor

$\overrightarrow{n}$ = $\begin{pmatrix}3\\2\\1\end{pmatrix}$ .
Die Angaben kannst du in die allgemeine Normalenform einer Ebenengleichung einsetzen und erhältst so die Gleichung zur Ebene $E$ in Normalenform:
$E: \overrightarrow{n} \circ \left( \overrightarrow{x} - \overrightarrow{p} \right)$ = $\left( \overrightarrow{x} - \begin{pmatrix}1\\1\\7\end{pmatrix} \right)\circ \begin{pmatrix}3\\2\\1\end{pmatrix}$ $=0$

Zunächst bestimmt man eine Parametergleichung der Ebene, dann einen Normalenvektor. Nun kann man eine Normalenform der Ebene aufstellen.

$R(-1\mid-2\mid3)$ , $S(2\mid1\mid0)$ , $T(-1\mid3\mid4)$ :

$E:\overrightarrow{x}= \left( {\begin{array}{c} -1 \\ -2 \\ 3 \\ \end{array}} \right) + ...$

Vollständige Lösung anzeigen

Den Normalenvektor berechnet man über das Kreuzprodukt der beiden Spannvektoren.

Kreuzprodukt bilden:

$\left( \begin{array}{c} 3 \\ 3 \\ -3 \\ \end{array} \right) \times \left( \begin{array}{c} 0 \\ 5 \\ 1 \\ \end{array} \right)$

$= \left( \begin{array}{c} 3\cdot 1 \\ -3 \cdot 0 \\ 3 \cdot 5 \\ \end{array} \right.\begin{array}{c} - \\ - \\ - \\ \end{array}\left. \begin{array}{c} (-3) \cdot 5 \\ 3\cdot 1\\ 0\cdot 3 \\ \end{array} \right)$ $= \left( \begin{array}{c} 18\\ -3 \\ 15 \\ \end{array} \right)$

Eine mögliche Normalenform ist somit:

$E:\;\left[ {\overrightarrow {x} - \left( {\begin{array}{c} { - 1} \\ { - 2} \\ 3 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} 18 \\ { - 3} \\ 15 \\ \end{array}} \right) = 0$

$A\left(1\mid4\mid2\right)$ , $E\left(-2\mid0\mid2\right)$ , $F\left(1\mid2\mid0\right)$ :

$E:\overrightarrow{x}= \left( {\begin{array}{c} 1 \\ 4 \\ 2 \\ \end{array}} \right) + ...$

Vollständige Lösung anzeigen

Den Normalenvektor berechnet man über das Kreuzprodukt der beiden Spannvektoren.

Kreuzprodukt bilden:

$\left( \begin{array}{r} -3 \\ -4 \\ 0 \\ \end{array} \right) \times \left( \begin{array}{r} 0 \\ 1 \\ 1 \\ \end{array} \right)$

$= \left( {\begin{array}{c} -4\cdot1 \\ 0\cdot0 \\ - 3\cdot1 \\ \end{array}}{\begin{array}{c} - \\ - \\ - \\ \end{array}}{\begin{array}{c} 0\cdot1 \\ (- 3)\cdot1 \\ (-4)\cdot0 \\ \end{array}} \right)$ $=\left( \begin{array}{r} -4 \\ 3 \\ -3 \\ \end{array} \right)$

Eine mögliche Normalenform ist somit:

$E:\;\left[ {\overrightarrow {x} - \left( {\begin{array}{c} { 1} \\ { 4} \\ 2 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} -4 \\ { 3} \\ - 3 \\ \end{array}} \right) = 0$

Um zu überprüfen, ob der Punkt in der Ebene liegt, setzt man seine Koordinaten in die Normalenform ein.

$A(1\mid2\mid-5)$ ,

$E:\;\left[ {\overrightarrow {x} - \left( {\begin{array}{c} { - 1} \\ { - 2} \\ 3 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} 6 \\ { - 1} \\ 5 \\ \end{array}} \right) = 0$ .

$\begin{array}{lll} E:&\left[ {\left( {\begin{array}{c} {1} \\ { 2} \\ -5 \\ \end{array}} \right) - \left( {\begin{array}{c} { - 1} \\ { - 2} \\ 3 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} 6 \\ { - 1} \\ 5 \\ \end{array}} \right) \\ &= 0 \\[5pt] \Leftrightarrow&\left[ {\left( {\begin{array}{c} {2} \\ { 4} \\ -8 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} 6 \\ { - 1} \\ 5 \\ \end{array}} \right) = 0 \end{array}$

Mit dem Skalarprodukt ergibt sich:

$2\cdot6+4\cdot(-1)+(-8)\cdot5$

$=12-4-40=(-32)\neq0$

Der Punkt $A$ liegt nicht in Ebene $E$ .

$P\left(-1\mid\frac{3}{4}\mid2\right)$ ,

$E:\;\left[ {\overrightarrow {x} - \left( {\begin{array}{c} { 1} \\ { 1} \\ 2 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} 1 \\ { - 8} \\ 2 \\ \end{array}} \right) = 0$ .

$\begin{array}{lll} E:&\left[ {\left( {\begin{array}{c} {-1} \\ {\frac{3}{4}} \\ 2 \\ \end{array}} \right) - \left( {\begin{array}{c} { 1} \\ { 1} \\ 2 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} 1 \\ { - 8} \\ 2 \\ \end{array}} \right) = 0 \\[5pt] \Leftrightarrow&\left[ {\left( {\begin{array}{c} {-2} \\ { -\frac{1}{4}} \\ 0 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} 1 \\ { - 8} \\ 2 \\ \end{array}} \right) = 0 \end{array}$

Mit dem Skalarprodukt ergibt sich:

$(-2)\cdot1+\left(-\dfrac{1}{4}\right)\cdot(-8)+0\cdot2$ $=(-2)+2+0=0$

Der Punkt $P$ liegt in der Ebene $E$ .

Setzt man die Koordinaten des gegebenen Punktes in die Normalenform ein ergibt sich:

$A(r\mid1\mid0)$ ,

$E:\;\left[ {\overrightarrow {x} - \left( {\begin{array}{c} { 1} \\ { 2} \\ 0 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} 1 \\ { 4} \\ -2 \\ \end{array}} \right) = 0$ .

$\begin{array}{ll} E:&\left[ {\left( {\begin{array}{c} {r} \\ {1} \\ 0 \\ \end{array}} \right) - \left( {\begin{array}{c} { 1} \\ { 2} \\ 0 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} 1 \\ { 4} \\ -2 \\ \end{array}} \right) = 0 \\[5pt] \Leftrightarrow&\left[ {\left( {\begin{array}{c} {r-1} \\ { -1} \\ 0 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} 1 \\ { 4} \\ -2 \\ \end{array}} \right) = 0 \end{array}$

Mit dem Skalarprodukt ergibt sich:

$r-1-4+0=0 \;\Leftrightarrow\; r=5$

Somit liegt der Punkt für $r=5$ in der Ebene.

$P\left(-1\mid r\mid2\right)$ ,

$E:\;\left[ {\overrightarrow {x} - \left( {\begin{array}{c} { 2} \\ { 1} \\ -1 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} 2 \\ { 1} \\ 2 \\ \end{array}} \right) = 0$ .

$\begin{array}{ll} E:&\left[ {\left( {\begin{array}{c} {-1} \\ {r} \\ 2 \\ \end{array}} \right) - \left( {\begin{array}{c} { 2} \\ { 1} \\ -1 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} 2 \\ { 1} \\ 2 \\ \end{array}} \right) = 0 \\[5pt] \Leftrightarrow&\left[ {\left( {\begin{array}{c} {-3} \\ { r-1} \\ 3 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} 2 \\ { 1} \\ 2 \\ \end{array}} \right) = 0 \end{array}$

Mit dem Skalarprodukt ergibt sich:

$-6+r-1+6=0 \;\Leftrightarrow\; r=1$

Somit liegt der Punkt für $r=1$ in der Ebene.

$P(2\mid0\mid4)$ ,

$E:\;\left[ {\overrightarrow {x} - \left( {\begin{array}{c} {1} \\ { r} \\ 2 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} 0 \\ { 2} \\ 5 \\ \end{array}} \right) = 0$ .

$\begin{array}{ll} E:&\left[ {\left( {\begin{array}{c} {2} \\ {0} \\ 4 \\ \end{array}} \right) - \left( {\begin{array}{c} { 1} \\ { r} \\ 2 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} 0 \\ { 2} \\ 5 \\ \end{array}} \right) = 0 \\[5pt] \Leftrightarrow&\left[ {\left( {\begin{array}{c} {1} \\ { -r} \\ 2 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} 0 \\ { 2} \\ 5 \\ \end{array}} \right) = 0 \end{array}$

Mit dem Skalarprodukt ergibt sich:

$0-2r+10=0 \;\Leftrightarrow\; r=5$

Somit liegt der Punkt für $r=5$ in der Ebene.

$Q\left(-1\mid1\mid6\right)$ ,

$E:\;\left[ {\overrightarrow {x} - \left( {\begin{array}{c} { 1} \\ {0} \\ 7 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} r \\ { 1} \\ 3 \\ \end{array}} \right) = 0$ .

$\begin{array}{ll} E:&\left[ {\left( {\begin{array}{c} {-1} \\ {1} \\ 6 \\ \end{array}} \right) - \left( {\begin{array}{c} { 1} \\ { 0} \\ 7 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} r \\ { 1} \\ 3 \\ \end{array}} \right) = 0 \\[5pt] \Leftrightarrow&\left[ {\left( {\begin{array}{c} {-2} \\ { 1} \\ -1 \\ \end{array}} \right) } \right] \circ \left( {\begin{array}{c} r \\ { 1} \\ 3 \\ \end{array}} \right) = 0 \end{array}$

Mit dem Skalarprodukt ergibt sich:

$-2r+1-3=0 \;\Leftrightarrow\; r=-1$

Somit liegt der Punkt für

$r=-1$

in der Ebene.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?