Lerninhalte in Mathe

Abi-Aufgaben

Digitales Schulbuch

Inhaltsverzeichnis

Punkt, Gerade und Ebene

1.

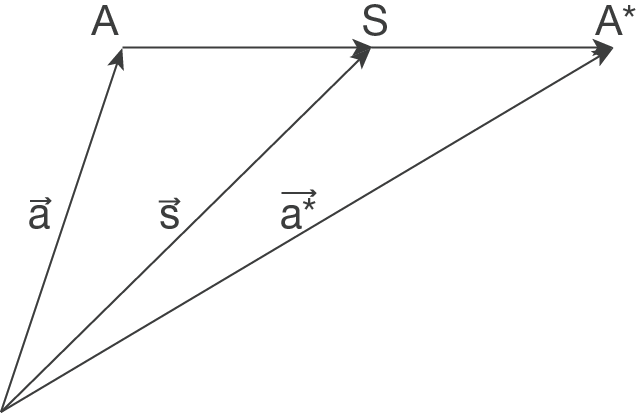
Punkt an Punkt spiegeln

Punkt $A(a_1\mid a_2 \mid a_3)$ an Punkt $B(b_1 \mid b_2 \mid b_3)$ spiegeln.

Gesucht: Punkt $A‘$

Verbindungsvektor $\vec{AB}$ bilden
$\vec{OA‘}=\vec{AB}+\vec{OB}$

2.

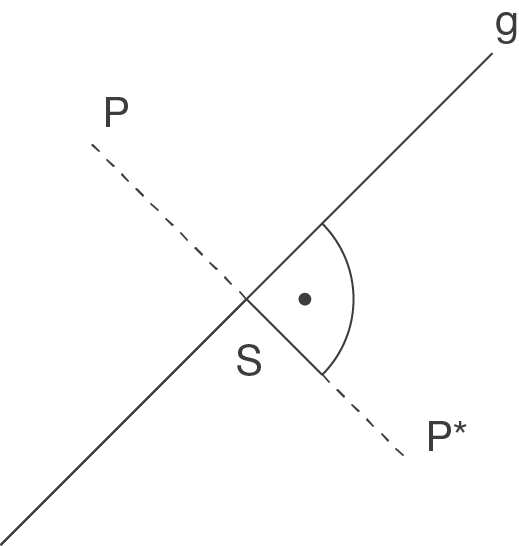
Punkt an Gerade spiegeln

Punkt $A(a_1\mid a_2 \mid a_3)$ an der Geraden g: $\vec{x}=\begin{pmatrix}s_1\\s_2\\s_3\end{pmatrix}+ t\cdot \begin{pmatrix}r_1\\r_2\\r_3\end{pmatrix}$ spiegeln.

Gesucht: $A‘$ .

allgemeiner Punkt $G$ der Geraden
$g$ bilden
Verbindungsvektor $\vec{AG}$ berechnen
Skalarprodukt von $\vec{AG}$ und Richtungsvektor von der Geraden $g$ bilden $\rightarrow$ lineares Gleichungssystem nach Parameter $t$ auflösen
Parameter $t$ in $\vec{AG}$ einsetzen
$\vec{AG}$ an $\vec{OA}$ addieren
Koordinaten von Punkt $A‘$ ablesen

3.

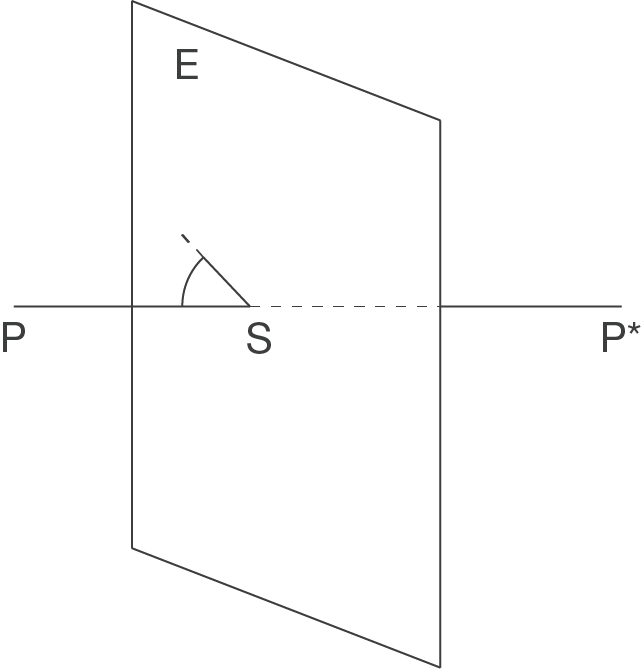
Punkt an Ebene spiegeln

Punkt $A(a_1\mid a_2 \mid a_3)$ an der Ebene E: $n_1\cdot x_1+n_2\cdot x_2+ n_3\cdot x_3=c$ spiegeln.

Gesucht: $A‘$

Hilfsgerade bilden
1. $\rightarrow$ durch Punkt $A$
2. $\rightarrow$ senkrecht zur Ebene $E$
Schnittpunkt $S$ zwischen der Hilfsgerade $g$ und der Ebene $E$ berechnen
Verbindungsvektor $\vec{AS}$ berechnen
$\overrightarrow{OA‘} = \overrightarrow{OS} + \overrightarrow{AS}$

1.

Verbindungsvektor $\overrightarrow{AS}$ aufstellen

Vektorkette $\overrightarrow{a^{*}}=\overrightarrow{s}+\overrightarrow{AS}$ bilden

Grafische Darstellung von Vektoren A, S, ā und ā* in einem Koordinatensystem.

a)

$\overrightarrow{AS}=\overrightarrow{s}-\overrightarrow{a}=\left( {\begin{array}{*{20}r} 2 \\ 4 \\ 8 \\ \end{array}} \right)-\left( {\begin{array}{*{20}r} 1 \\ 2 \\ 4 \\ \end{array}} \right)=\left( {\begin{array}{*{20}r} 1 \\ 2 \\ 4 \\ \end{array}} \right)$

$A^*(3|6|12)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

b)

$\overrightarrow{AS}=\left( {\begin{array}{*{20}r} -5 \\ 0 \\ -4 \\ \end{array}} \right)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$A^*(-9|2|-4)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

c)

$\overrightarrow{AS}=\left( {\begin{array}{*{20}r} -2 \\ 0 \\ -3 \\ \end{array}} \right)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$A^*(-3|2|-2)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

d)

$\overrightarrow{AS}=\left( {\begin{array}{*{20}r} -3 \\ 0 \\ 0 \\ \end{array}} \right)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$A^*(-5|2|4)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

2.

Normalenvektor $\overrightarrow{n}$ der Ebene bilden

Gerade durch $P$ mit Richtungsvektor $\overrightarrow{n}$ aufstellen

Gerade mit Ebene schneiden lassen ergibt den Schnittpunkt $S$

Verbindungsvektor $\overrightarrow{PS}$ aufstellen

Vektorkette $\overrightarrow{p^*}=\overrightarrow{s}+\overrightarrow{PS}$ bilden (vgl. Lösungsskizze zu 1.)

Diagramm mit Linien und einem Winkel zwischen den Elementen P, S und E.

a)

Spiegelpunkt $P*$ berechnen:

Gerade durch $P$ , senkrecht zu $E$ :

$\overrightarrow{n}=\left( {\begin{array}{*{20}r} 2 \\ -2 \\ 1 \\ \end{array}} \right)$

$\Rightarrow g: \overrightarrow{x}=\left( {\begin{array}{*{20}r} 2 \\ 1 \\ 6 \\ \end{array}} \right)+s\cdot\left( {\begin{array}{*{20}r} 2 \\ -2 \\ 1 \\ \end{array}} \right)$

(durch Ablesen aus der
Koordinatenform der Ebene)

Schnittpunkt von $g$ mit $E$ ( $g$ in $E$ einsetzen)

$\begin{array}{ll} s=1 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$s=1$ in $g$ eingesetzt, ergibt:

$S(4|-1|7)$ und somit den Verbindungsvektor $\overrightarrow{PS}=\left( {\begin{array}{*{20}r} 2 \\ -2 \\ 1 \\ \end{array}} \right)$

$P^*(6|-3|8)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

b)

Spiegelpunkt $P*$ berechnen:

Gerade durch $P$ , senkrecht zu $E$ :

$\overrightarrow{n}=\left( {\begin{array}{*{20}r} 1 \\ 1 \\ -1 \\ \end{array}} \right)$

$\Rightarrow g: \overrightarrow{x}=\left( {\begin{array}{*{20}r} 1 \\ 2 \\ -2 \\ \end{array}} \right)+s\cdot\left( {\begin{array}{*{20}r} 1 \\ 1 \\ -1 \\ \end{array}} \right)$

(durch Ablesen aus der
Koordinatenform der Ebene)

Schnittpunkt von $g$ mit $E$ ( $g$ in $E$ einsetzen)

$\begin{array}{ll} s=-1 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$s$ in $g$ :

$S(0|1|-1)$ $\;\Rightarrow\overrightarrow{PS}=\left( {\begin{array}{*{20}r} -1 \\ -1 \\ 1 \\ \end{array}} \right)$

$P^*(-1|0|0)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

c)

Spiegelpunkt $P*$ berechnen:

Gerade durch $P$ , senkrecht zu $E$ :

$\overrightarrow{n}=\left( {\begin{array}{*{20}r} 1 \\ 2\\ -1 \\ \end{array}} \right)$

$\Rightarrow g: \overrightarrow{x}=\left( {\begin{array}{*{20}r} -2 \\ 2 \\ -1 \\ \end{array}} \right)+s\cdot\left( {\begin{array}{*{20}r} 1 \\ 2 \\ -1 \\ \end{array}} \right)$

(durch Ablesen aus der
Koordinatenform der Ebene)

Schnittpunkt von $g$ mit $E$ ( $g$ in $E$ einsetzen):

$\begin{array}{ll} s=-\dfrac{1}{3} \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$s$ in $g$ :

$S\left(-\dfrac{7}{3}\mid\dfrac{4}{3}\mid-\dfrac{2}{3}\right)$ $\;\Rightarrow\overrightarrow{PS}=\left( {\begin{array}{*{20}r} -\frac{1}{3} \\ -\frac{2}{3} \\ \frac{1}{3} \\ \end{array}} \right)$

$P^*\left(-\frac{8}{3}\mid\frac{2}{3}\mid-\frac{1}{3}\right)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

d)

Spiegelpunkt $P*$ berechnen:

Gerade durch $P$ , senkrecht zu $E$ :

$\overrightarrow{n}=\left( {\begin{array}{*{20}r} -1 \\ -2 \\ 2 \\ \end{array}} \right)$

$\Rightarrow g: \overrightarrow{x}=\left( {\begin{array}{*{20}r} -2 \\ 0 \\ 4 \\ \end{array}} \right)+s\cdot\left( {\begin{array}{*{20}r} -1 \\ -2 \\ 2 \\ \end{array}} \right)$

(durch Ablesen aus der
Koordinatenform der Ebene)

Schnittpunkt von $g$ mit $E$ ( $g$ in $E$ einsetzen):

$\begin{array}{ll} s=1 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$s$ in $g$ :

$S(-3|-2|6)$ $\;\Rightarrow\overrightarrow{PS}=\left( {\begin{array}{*{20}r} -1 \\ -2 \\ 2 \\ \end{array}} \right)$

$P^*(-4|-4|8)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

3.

Punkt $S$ auf $g$ in Abhängigkeit von $s$ bestimmen
Verbindungsvektor $\overrightarrow{PS}$ erstellen
Skalarprodukt von $\overrightarrow{PS}$ mit dem Richtungsvektor der Geraden gleich Null setzen (stehen senkrecht aufeinander) und damit $s$ bestimmen.
$s$ führt uns zu $S$ und $\overrightarrow{PS}$
Vektorkette $\overrightarrow{p^*}=\overrightarrow{s}+\overrightarrow{PS}$ bilden (vgl. Lösungsskizze zu 1.)

Diagramm mit Linien P, S und g sowie einem Punkt S und einem Winkel.

a)

1. $S$ , $\overrightarrow{PS}$ allgemein bestimmen:

$S(2+2s|1+2s|s)$ (durch Ablesen von g)

$\overrightarrow{PS}=\left( {\begin{array}{*{20}r} 2+2s-2 \\ 1+2s-1 \\ s-6 \\ \end{array}} \right)=\left( {\begin{array}{*{20}r} 2s \\ 2s \\ s-6 \\ \end{array}} \right)$

2. $S$ , $\overrightarrow{PS}$ konkret bestimmen:

$\overrightarrow{PS}\cdot\overrightarrow{v_g}=$ $\left( {\begin{array}{*{20}r} 2s \\ 2s \\ s-6 \\ \end{array}} \right)\cdot\left( {\begin{array}{*{20}r} 2 \\ 2 \\ 1 \\ \end{array}} \right)=0$

$\begin{array}{rll} 4s+4s+s-6&=&0&\\ 9s&=&6& \\ s&=&\dfrac{2}{3}& \\ \end{array}$

$s=\dfrac{2}{3}$ in $S$ und $\overrightarrow{PS}$ eingesetzt, ergibt:

$S\left(\frac{10}{3}\mid\frac{7}{3}\mid\frac{2}{3}\right)$ $\;\Rightarrow\overrightarrow{PS}=\left( {\begin{array}{*{20}r} \frac{4}{3} \\ \frac{4}{3} \\ -\frac{16}{3} \\ \end{array}} \right)$

$P^*\left(\dfrac{14}{3}\mid\dfrac{11}{3}\mid-\dfrac{14}{3}\right)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

b)

1. $S$ , $\overrightarrow{PS}$ allgemein bestimmen:

$S(1-s|4|2+s)$ (durch Ablesen von g)

$\overrightarrow{PS}=\left( {\begin{array}{*{20}r} 1-s-1 \\ 4-(-2) \\ 2+s-4 \\ \end{array}} \right)=\left( {\begin{array}{*{20}r} -s \\ 6 \\ s-2 \\ \end{array}} \right)$

2. $S$ , $\overrightarrow{PS}$ konkret bestimmen:

$\overrightarrow{PS}\cdot\overrightarrow{v_g}=$ $\left( {\begin{array}{*{20}r} -s \\ 6 \\ s-2 \\ \end{array}} \right)\cdot\left( {\begin{array}{*{20}r} -1 \\ 0 \\ 1 \\ \end{array}} \right)=0$

$\begin{array}{rcll} s+s-2&=&0&\\ 2s&=&2&\\ s&=&1& \\ \end{array}$

$s=1$ in $S$ und $\overrightarrow{PS}$ eingesetzt, ergibt:

$S\left(0|4|3\right)$ $\;\Rightarrow\overrightarrow{PS}=\left( {\begin{array}{*{20}r} -1 \\ 6 \\ -1 \\ \end{array}} \right)$

$P^*\left(-1|10|2\right)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

c)

1. $S$ , $\overrightarrow{PS}$ allgemein bestimmen:

$S(2-2s|4+s|0)$ (durch Ablesen von g)

$\overrightarrow{PS}=\left( {\begin{array}{*{20}r} 2-2s-1 \\ 4+s-1 \\ -2 \\ \end{array}} \right)=\left( {\begin{array}{*{20}r} 1-2s \\ 3+s \\ -2 \\ \end{array}} \right)$

2. $S$ , $\overrightarrow{PS}$ konkret bestimmen:

$\overrightarrow{PS}\cdot\overrightarrow{v_g}=$ $\left( {\begin{array}{*{20}r} 1-2s \\ 3+s \\ -2 \\ \end{array}} \right)\cdot\left( {\begin{array}{*{20}r} -2 \\ 1 \\ 0 \\ \end{array}} \right)=0$

$\begin{array}{rcll} -2+4s+3+s&=&0&\\ 5s&=&-1&\\ s&=&-\dfrac{1}{5}& \\ \end{array}$

$s=-\dfrac{1}{5}$ in $S$ und $\overrightarrow{PS}$ eingesetzt, ergibt:

$S\left(\frac{12}{5}\mid\frac{19}{5}\mid0\right)$ $\;\Rightarrow\overrightarrow{PS}=\left( {\begin{array}{*{20}r} \frac{7}{5} \\ \frac{14}{5} \\ -2 \\ \end{array}} \right)$

$P^*\left(\dfrac{19}{5}\mid\dfrac{33}{5}\mid-2\right)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

d)

1. $S$ , $\overrightarrow{PS}$ allgemein bestimmen:

$S(1+s|1-2s|s)$ (durch Ablesen von g)

$\overrightarrow{PS}=\left( {\begin{array}{*{20}r} 1+s-1 \\ 1-2s-0 \\ s-4 \\ \end{array}} \right)=\left( {\begin{array}{*{20}r} s \\ 1-2s \\ s-4 \\ \end{array}} \right)$

2. $S$ , $\overrightarrow{PS}$ konkret bestimmen:

$\overrightarrow{PS}\cdot\overrightarrow{v_g}=$ $\left( {\begin{array}{*{20}r} s \\ 1-2s \\ s-4 \\ \end{array}} \right)\cdot\left( {\begin{array}{*{20}r} 1 \\ -2 \\ 1 \\ \end{array}} \right)=0$

$\begin{array}{rcll} s-2+4s+s-4&=&0&\\ 6s&=&6& \\ s&=&1& \\ \end{array}$

$s=1$ in $S$ und $\overrightarrow{PS}$ eingesetzt, ergibt:

$S\left(2|-1|1\right)$ $\;\Rightarrow\overrightarrow{PS}=\left( {\begin{array}{*{20}r} 1 \\ -1 \\ -3 \\ \end{array}} \right)$

$P^*\left(3|-2|-2\right)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?