Gebrochenrationale Funktionen
Gebrochenrationale Funktionen besitzen ganzrationale Funktionen im Zähler sowie im Nenner, sind also Funktionen der Form:
 Um eine Funktionsgleichung anhand eines gegebenen Schaubildes aufzustellen, ist oft folgender Ansatz nützlich:
Um eine Funktionsgleichung anhand eines gegebenen Schaubildes aufzustellen, ist oft folgender Ansatz nützlich:

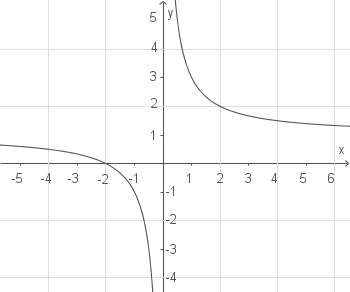
: Polstelle
- Vorzeichenwechsel (VZW) an der Stelle
;
kein VZW
: Verschiebung in
-Richtung (Asymptote)
: Setze in die Funktionsgleichung die Koordinaten eines gut ablesbaren Punktes ein
Beispiel

Wähle den Ansatz: 


- VZW
- Polstelle bei
- waagrechte Asymptote bei
- Punkt
einsetzen:
1.
Gegeben sind die Schaubilder einiger Funktionen. Bestimme einen möglichen Funktionsterm.
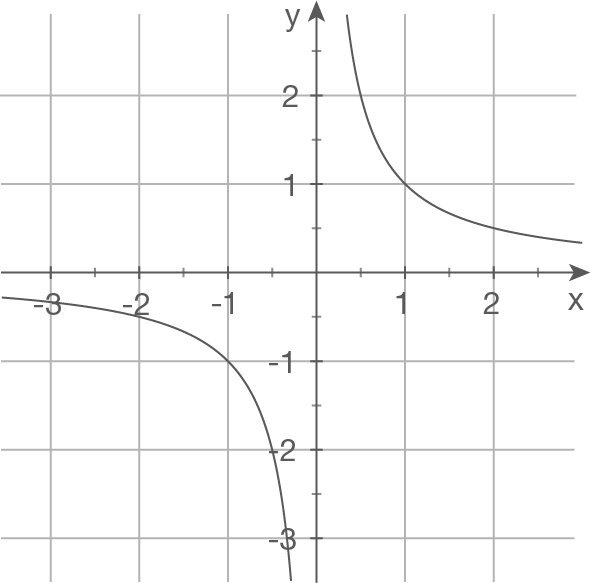
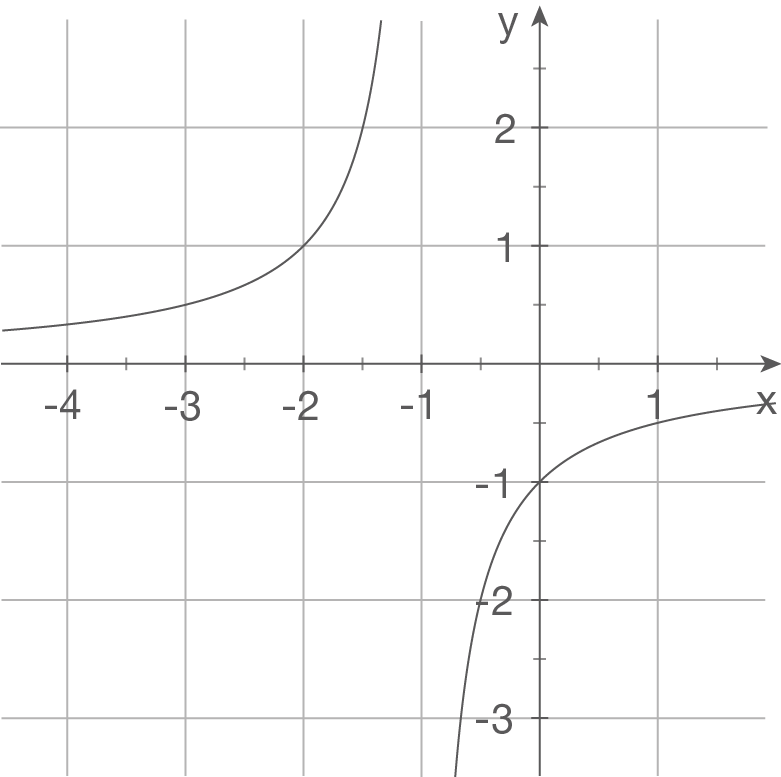
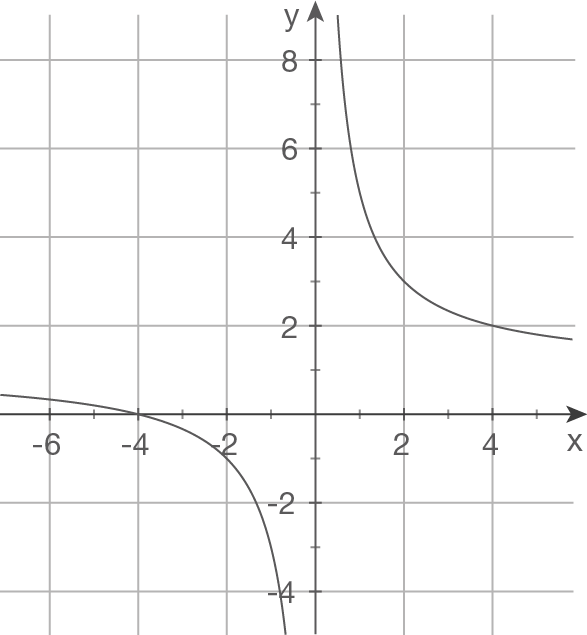
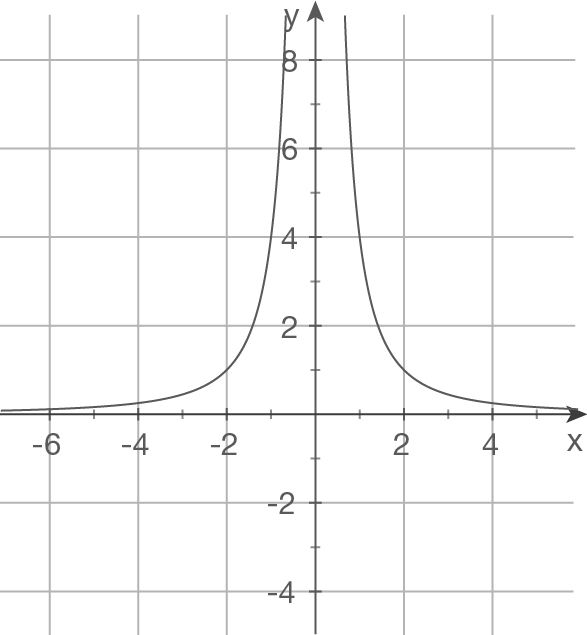
a)

b)

c)

d)

2.
Gegeben sind die Schaubilder einiger Funktionen. Bestimme einen möglichen Funktionsterm.
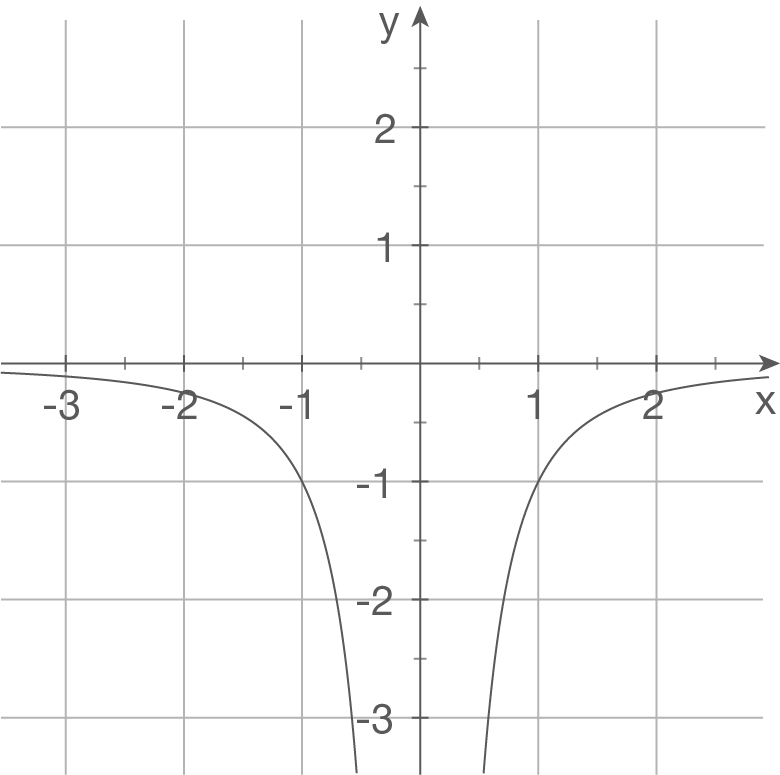
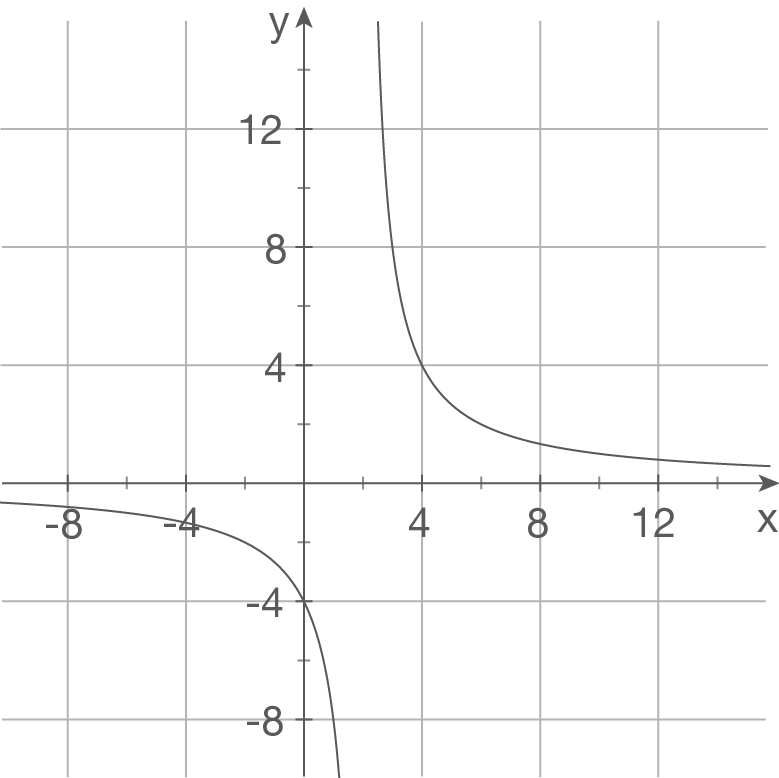
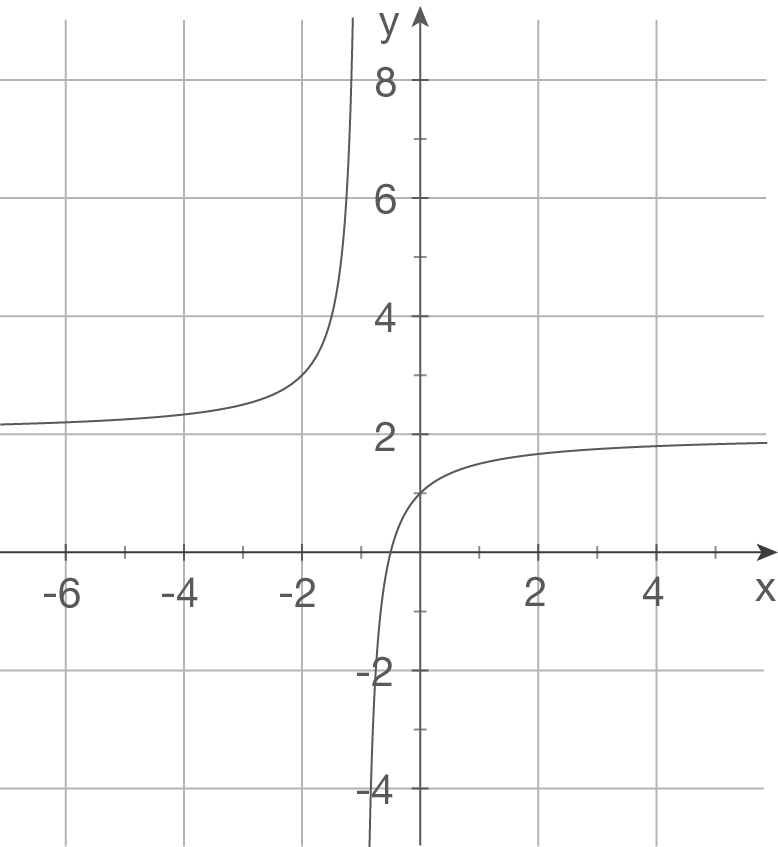
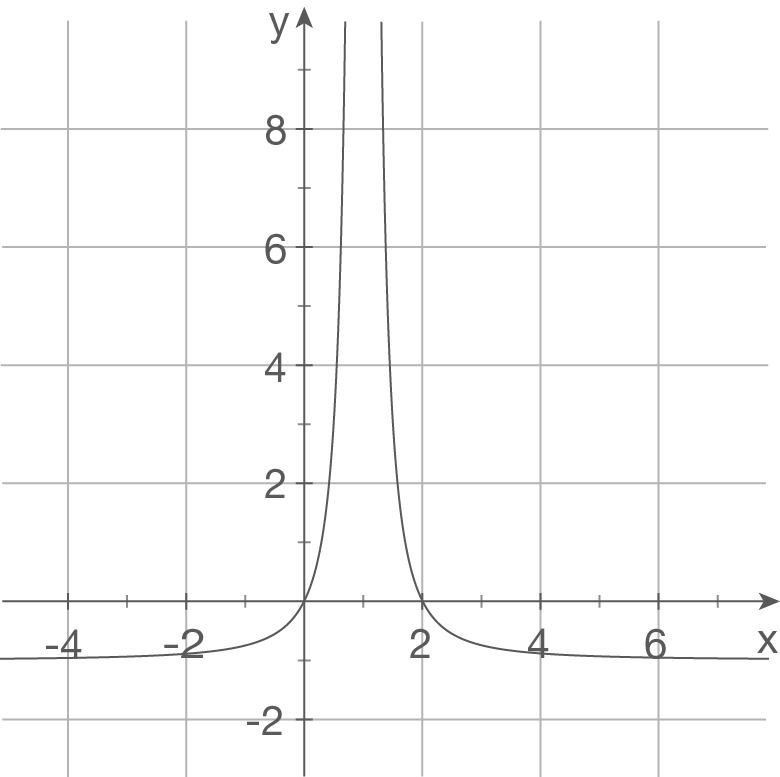
a)

b)

c)

d)

3.
Gegeben sind die Schaubilder einiger Funktionen. Bestimme einen möglichen Funktionsterm.
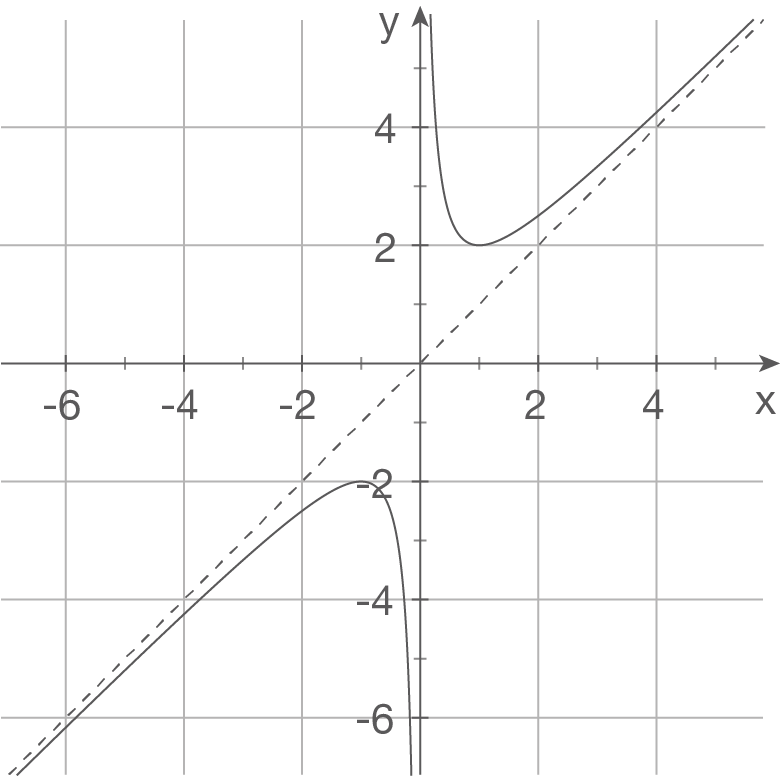
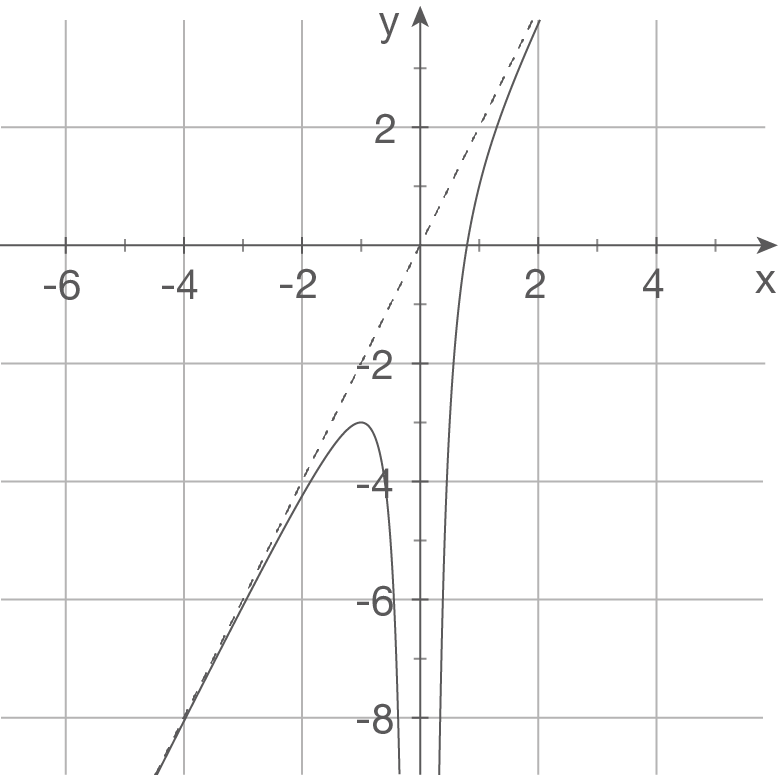
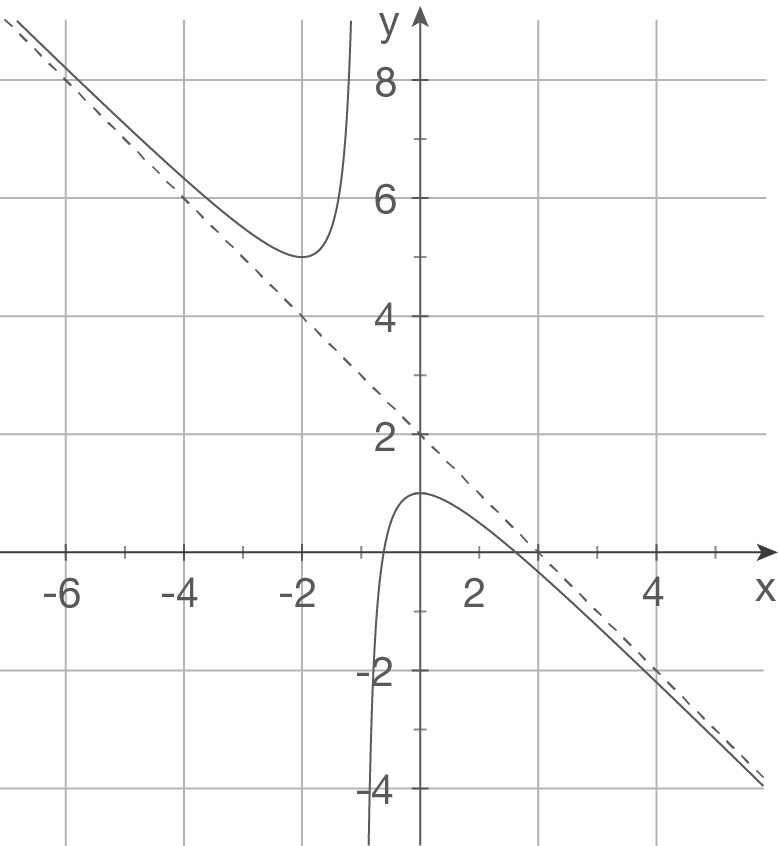
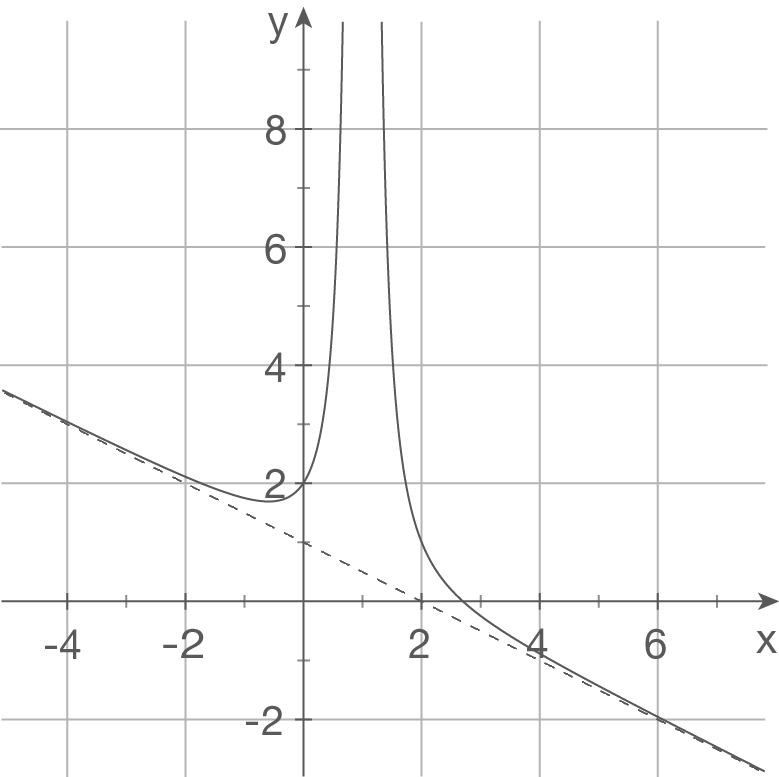
a)

b)

c)

d)

e)

f)

Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
Bei dieser Aufgabe brauchst du einen allgemeinen Ansatz. Mithilfe von Punkten, Polstellen und Asymptoten kann man dann die Funktionsgleichung näher bestimmen.
Der allgemeine Ansatz lautet
 mit
mit  falls ein VZW vorliegt und
falls ein VZW vorliegt und  falls kein VZW vorliegt.
Dabei beschreibt
falls kein VZW vorliegt.
Dabei beschreibt  die Verschiebung in
die Verschiebung in  -Richtung und
-Richtung und  die Verschiebung in
die Verschiebung in  -Richtung. Die Werte von
-Richtung. Die Werte von  und
und  müssen anhand von Polstellen und Asymptoten entsprechend bestimmt werden. Die Polstelle sind die Stellen, an denen der Nenner gleich Null ist. Eine Asymptote liegt vor, falls sich die Funktion für
müssen anhand von Polstellen und Asymptoten entsprechend bestimmt werden. Die Polstelle sind die Stellen, an denen der Nenner gleich Null ist. Eine Asymptote liegt vor, falls sich die Funktion für  einer Geraden (waagrechte oder schiefe Asymptote) annähert.
einer Geraden (waagrechte oder schiefe Asymptote) annähert.
1.
a)
Ansatz:  Polstelle bei
Polstelle bei  waagrechte Asymptote bei
waagrechte Asymptote bei

 eingesetzt:
eingesetzt:  Funktionsgleichung:
Funktionsgleichung: 
b)
Ansatz:  Polstelle bei
Polstelle bei  waagrechte Asymptote
bei
waagrechte Asymptote
bei 
 eingesetzt:
eingesetzt:  Funktionsgleichung:
Funktionsgleichung: 
c)
Ansatz:  Polstelle bei
Polstelle bei  waagrechte Asymptote
bei
waagrechte Asymptote
bei 
 eingesetzt:
eingesetzt:  Funktionsgleichung:
Funktionsgleichung: 
d)
Ansatz:  (da kein VZW)
Polstelle bei
(da kein VZW)
Polstelle bei  waagrechte Asymptote
bei
waagrechte Asymptote
bei 
 eingesetzt:
eingesetzt:  Funktionsgleichung:
Funktionsgleichung: 
2.
a)
Ansatz:  (da kein VZW)
Polstelle bei
(da kein VZW)
Polstelle bei  waagrechte Asymptote bei
waagrechte Asymptote bei 
 eingesetzt:
eingesetzt:  Funktionsgleichung:
Funktionsgleichung: 
b)
Ansatz:  Polstelle bei
Polstelle bei  waagrechte Asymptote bei
waagrechte Asymptote bei

 eingesetzt:
eingesetzt:  Funktionsgleichung:
Funktionsgleichung: 
c)
Ansatz:  Polstelle bei
Polstelle bei  waagrechte Asymptote bei
waagrechte Asymptote bei

 eingesetzt:
eingesetzt:  Funktionsgleichung:
Funktionsgleichung:

d)
Ansatz:  (da kein VZW)
Polstelle bei
(da kein VZW)
Polstelle bei  waagrechte Asymptote bei
waagrechte Asymptote bei 
 eingesetzt:
eingesetzt:

 Funktionsgleichung:
Funktionsgleichung:

3.
a)
Ansatz:  Polstelle bei
Polstelle bei  schiefe Asymptote mit
schiefe Asymptote mit 
 eingesetzt:
eingesetzt:  Funktionsgleichung:
Funktionsgleichung:

b)
Ansatz:
 (da kein VZW)
Polstelle bei
(da kein VZW)
Polstelle bei  schiefe Asymptote mit
schiefe Asymptote mit 
 eingesetzt:
eingesetzt:


 Funktionsgleichung:
Funktionsgleichung:

c)
Ansatz:  Polstelle bei
Polstelle bei  schiefe Asymptote mit
schiefe Asymptote mit 
 eingesetzt:
eingesetzt:

 Funktionsgleichung:
Funktionsgleichung:

d)
Ansatz:  (da kein VZW)
Polstelle bei
(da kein VZW)
Polstelle bei  schiefe Asymptote mit
schiefe Asymptote mit

 eingesetzt:
eingesetzt:



 Funktionsgleichung:
Funktionsgleichung:

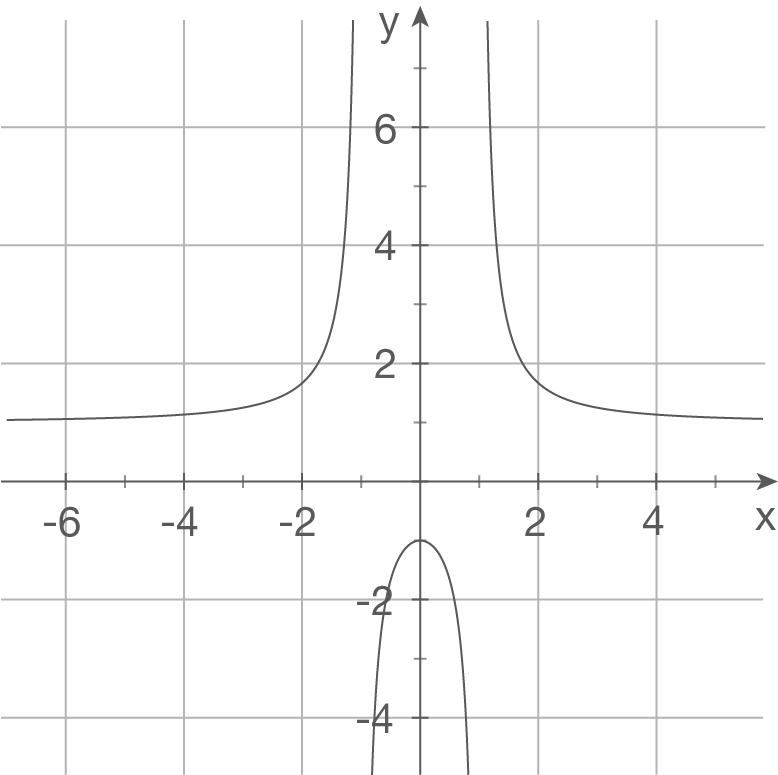
e)
Ansatz:
 (da zwei Polstellen)
Polstelle bei
(da zwei Polstellen)
Polstelle bei  und
und  und
und  waagrechte Asymptote bei
waagrechte Asymptote bei

 eingesetzt:
eingesetzt:


 Funktionsgleichung:
Funktionsgleichung:


 (3. Binomische Formel)
(3. Binomische Formel)


 (3. Binomische Formel)
(3. Binomische Formel)
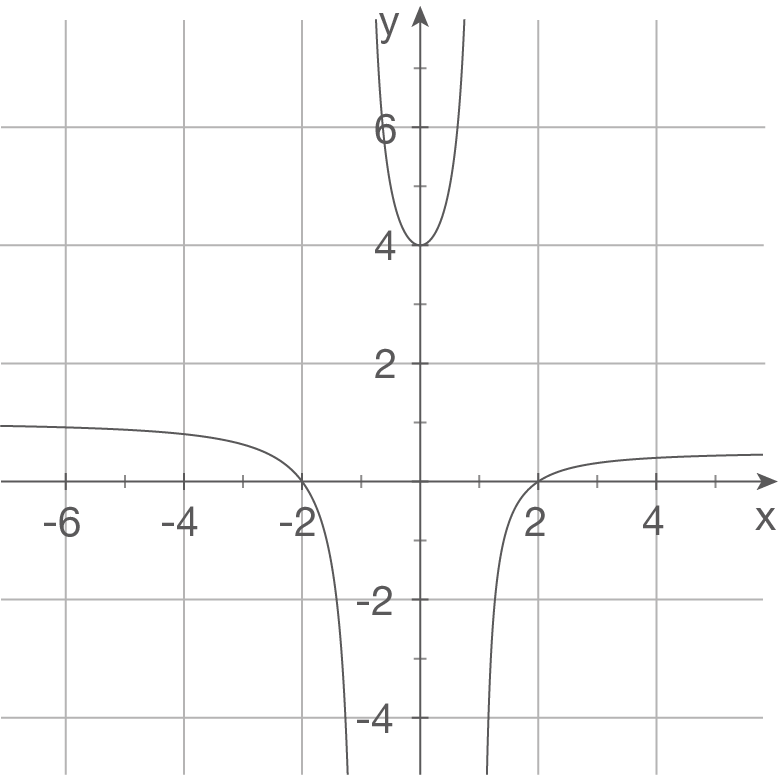
f)
Ansatz:
 (da zwei Polstellen)
Polstelle bei
(da zwei Polstellen)
Polstelle bei  und
und  und
und  waagrechte Asymptote bei
waagrechte Asymptote bei 
 eingesetzt:
eingesetzt:



 Funktionsgleichung:
Funktionsgleichung:

