Graphisches Ableiten
Eine Funktion  kannst du auch graphisch ableiten. Mit Hilfe der Eigenschaften von
kannst du auch graphisch ableiten. Mit Hilfe der Eigenschaften von  kannst du Aussagen über die erste Ableitung der Funktion
kannst du Aussagen über die erste Ableitung der Funktion  machen.
machen.
 wird graphisch abgeleitet.
wird graphisch abgeleitet.
| f(x) | f‘(x) |
|---|---|
| Steigung positiv | Graph oberhalb der |
| Steigung negativ | Graph unterhalb der |
| Extremstellen | Nullstellen |
| Wendepunkte | Extrempunkte/ Sattelpunkte |
Beispiel
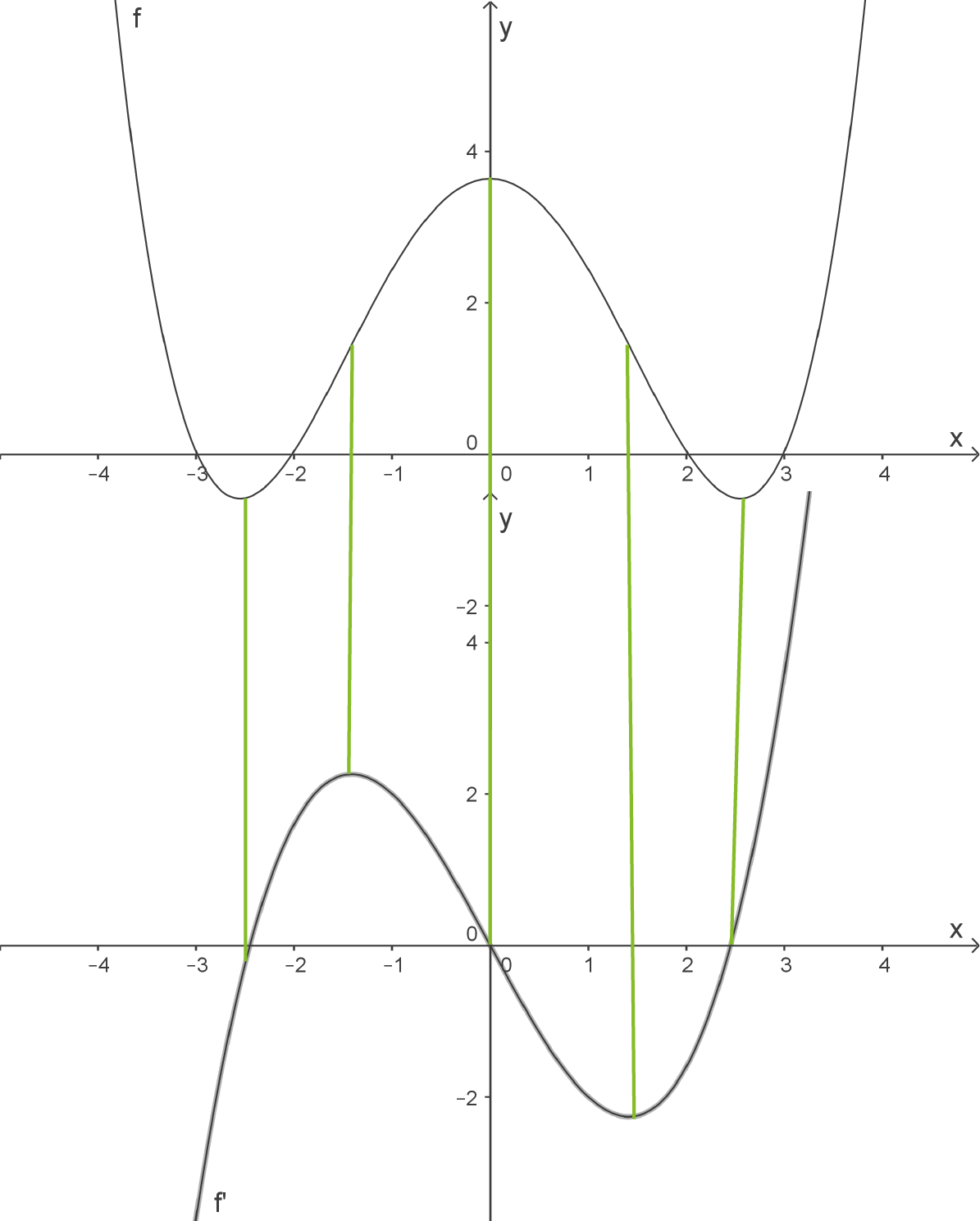
Das Schaubild der Funktion
1.
Die unten stehenden Abbildungen stellen die Graphen der Ableitungsfunktionen der angegeben Funktionen dar.
Ordne die Abbildungen den passenden Funktionen zu.
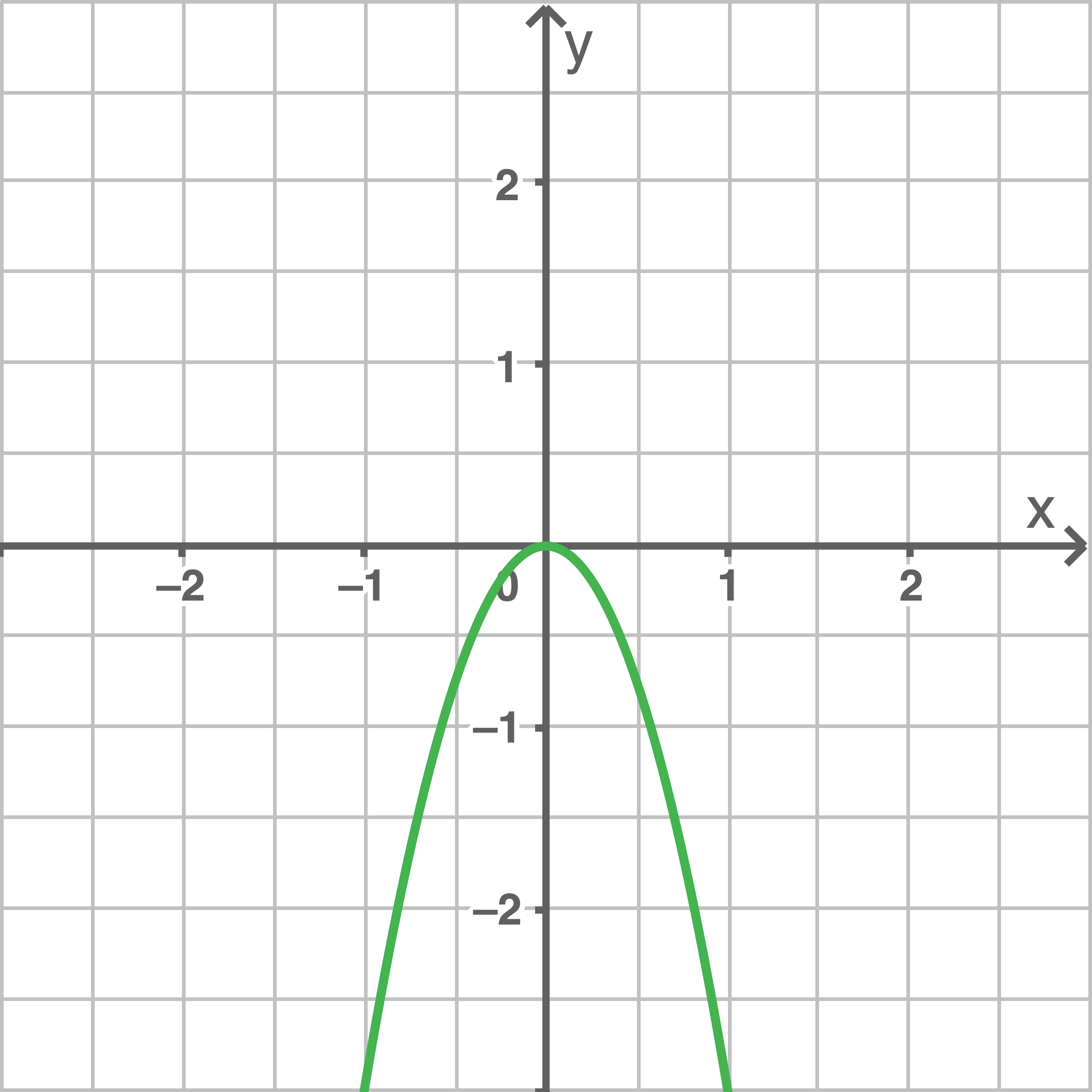
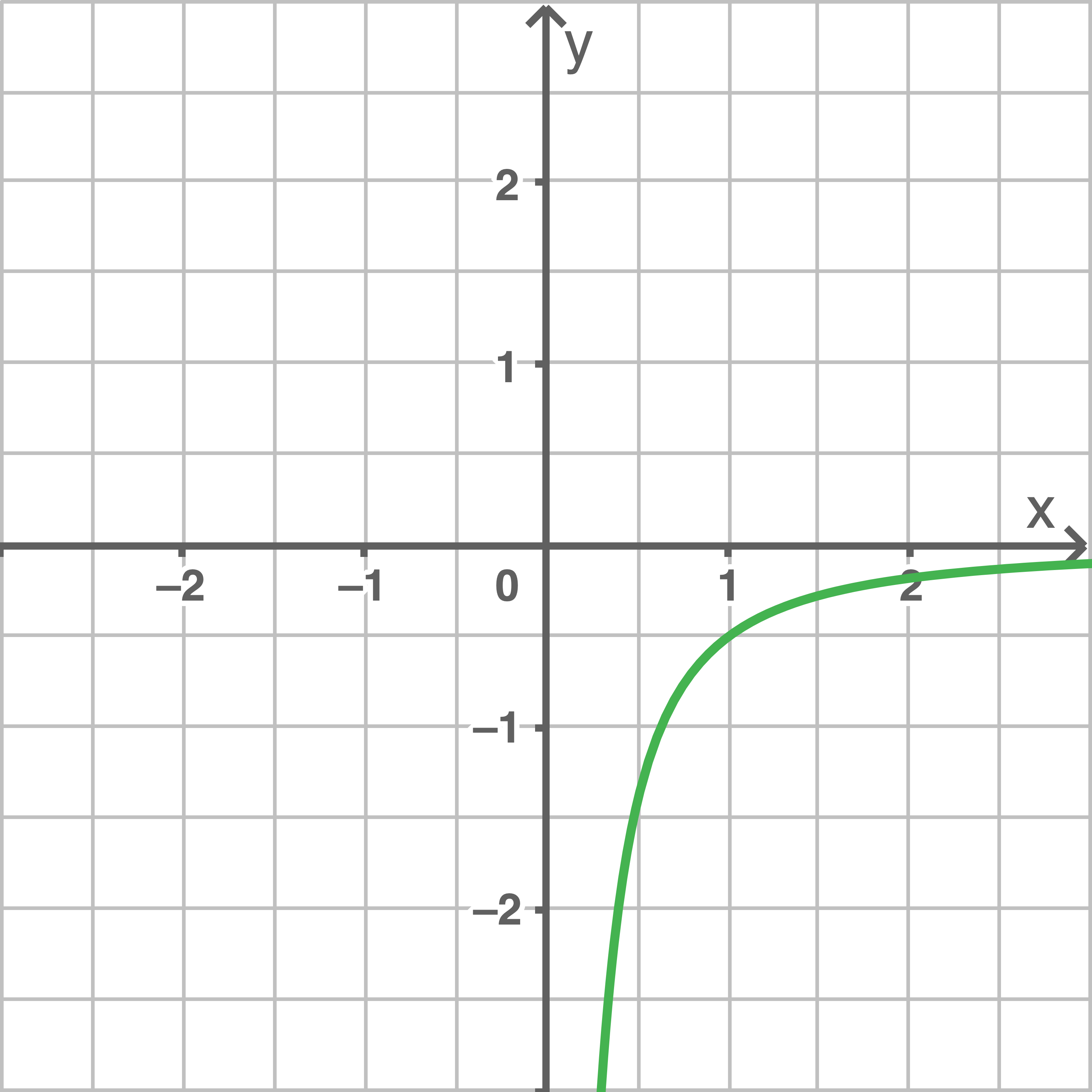

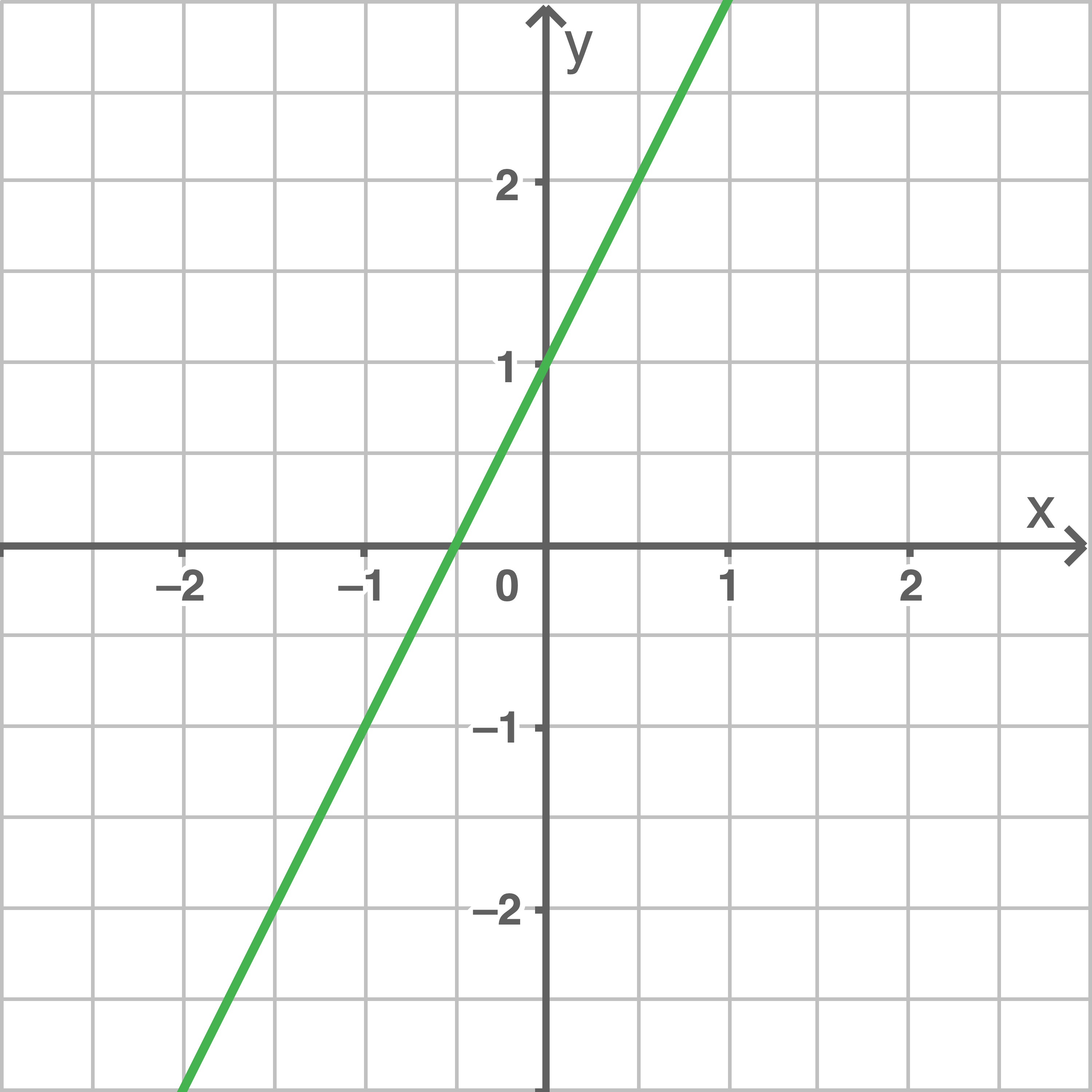
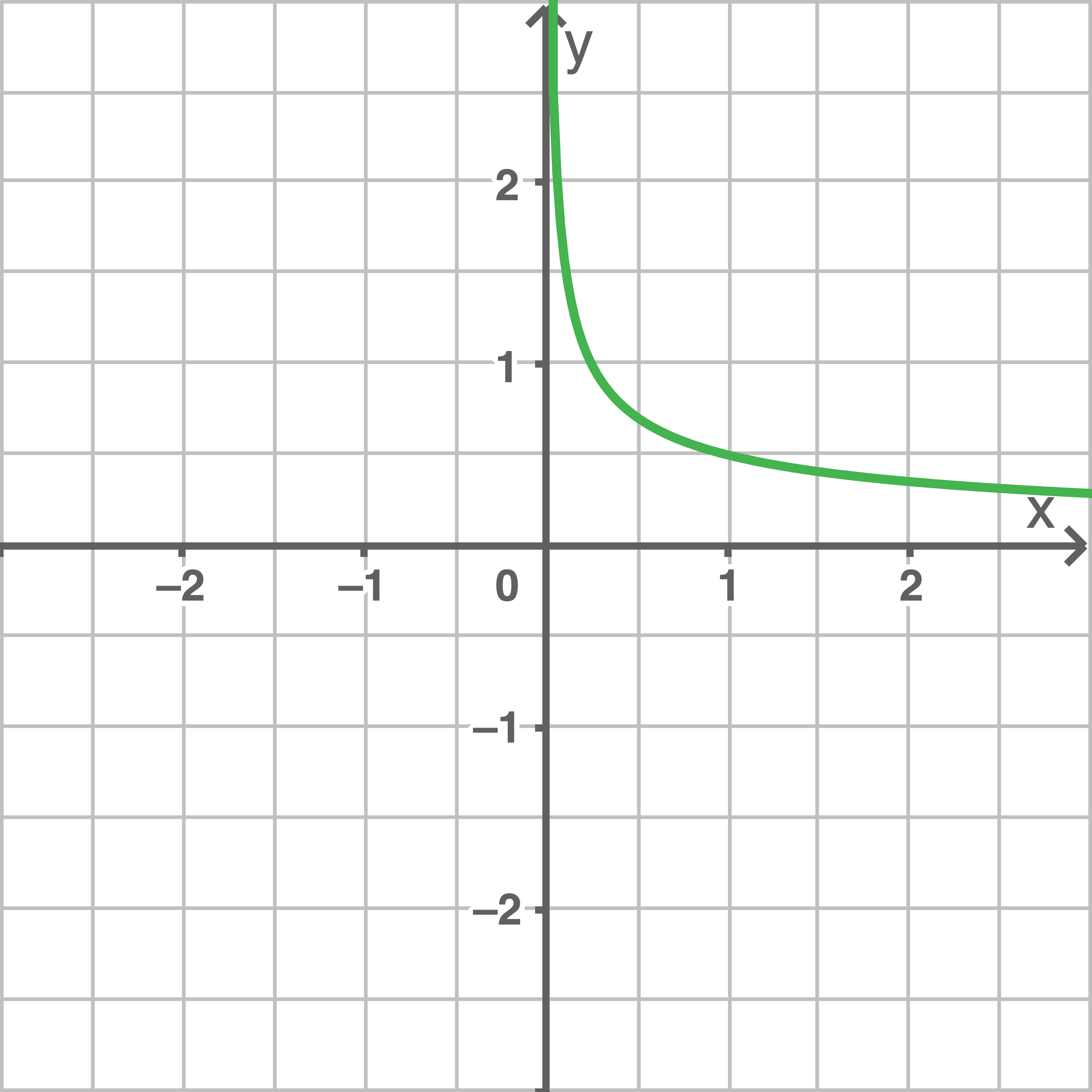
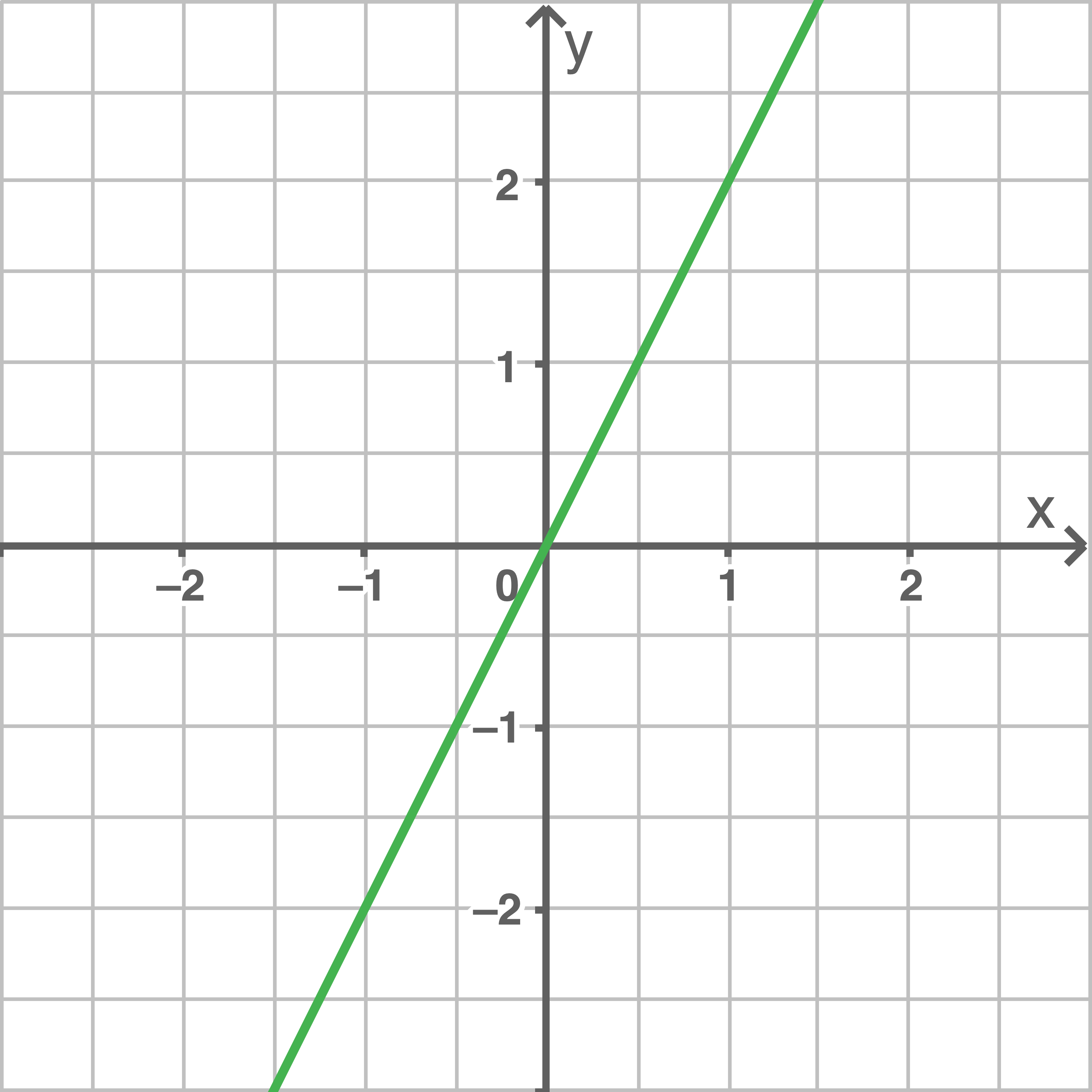
Ordne die Abbildungen den passenden Funktionen zu.
(A)

(B)

(C)

(D)

(E)

(F)

2.
Die Abbildungen zeigen jeweils den Graphen einer differenzierbaren Funktion 
Zeichne jeweils den Graphen der Ableitungsfunktion in das Koordinatensystem der Abbildungen.
Hinweis: Hier eignet sich ein Export in Apps wie GoodNotes oder Notability.
in das Koordinatensystem der Abbildungen.
Hinweis: Hier eignet sich ein Export in Apps wie GoodNotes oder Notability.
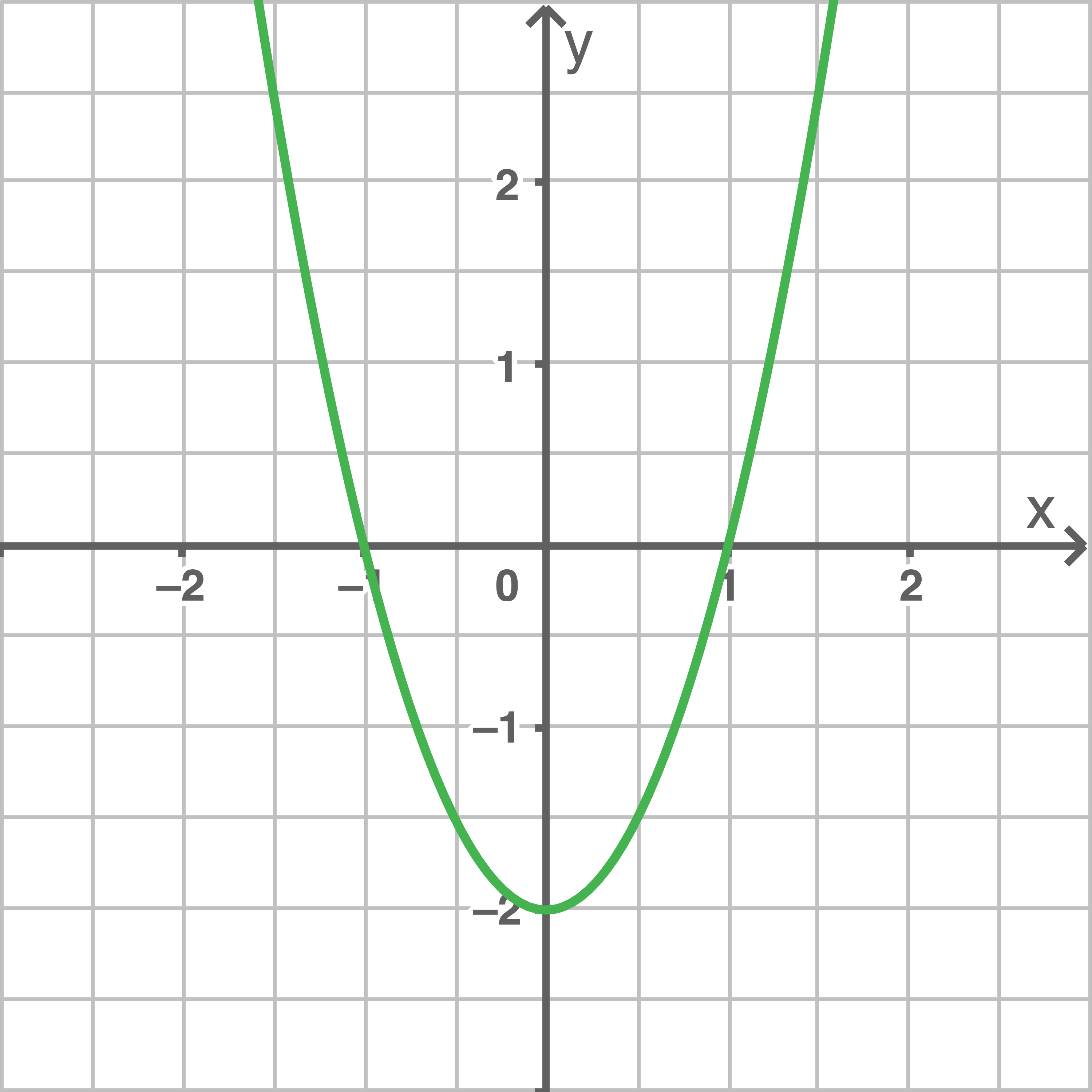
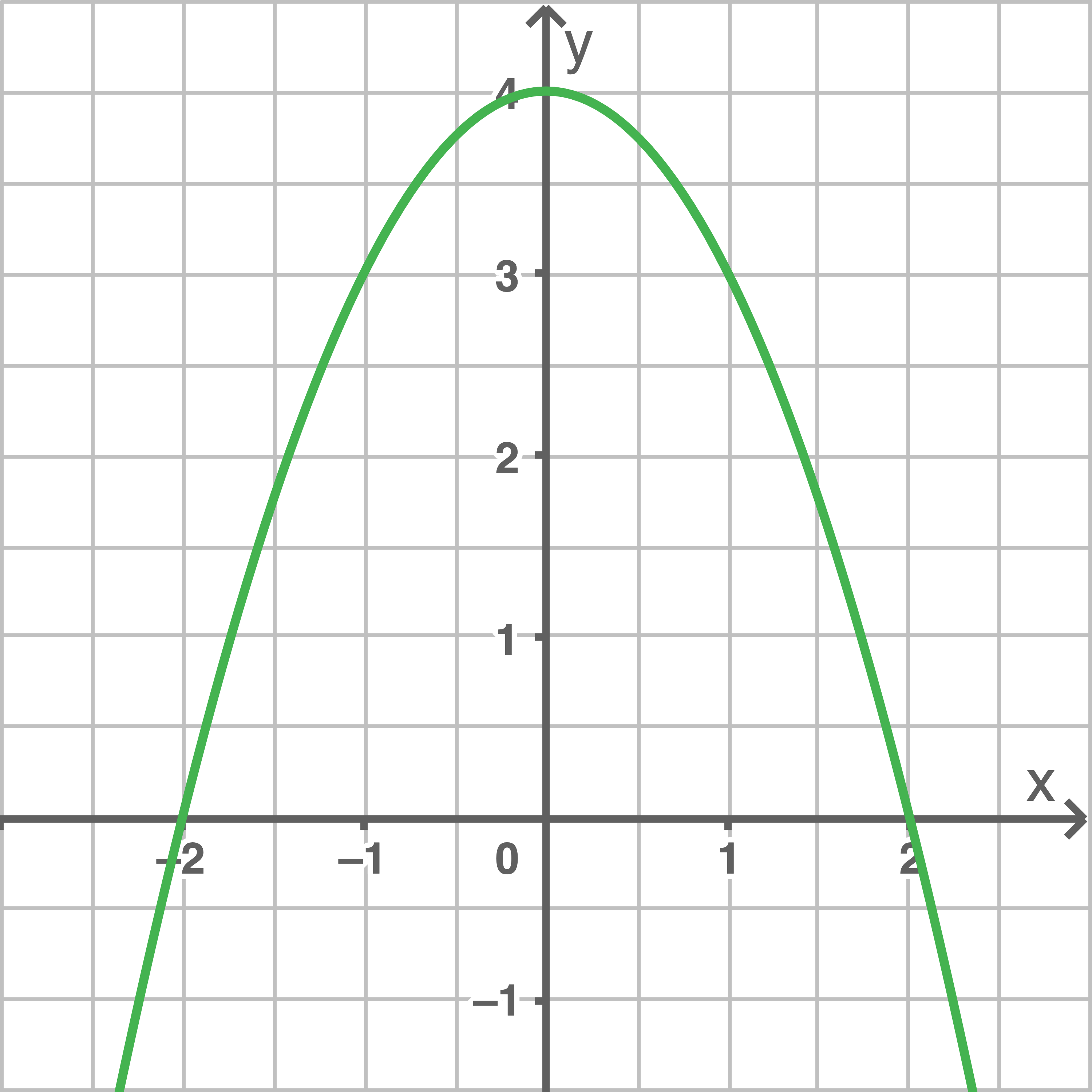
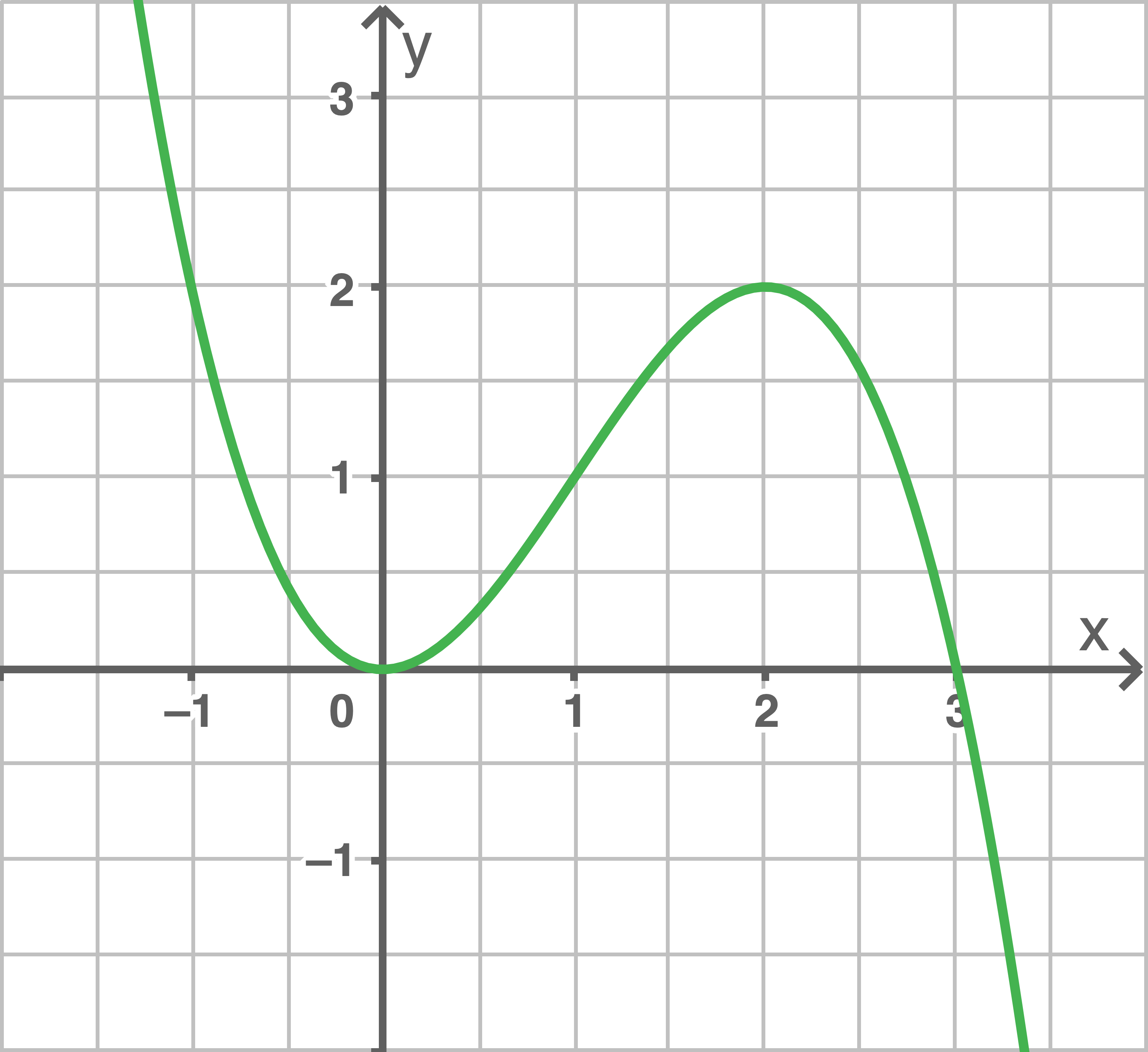
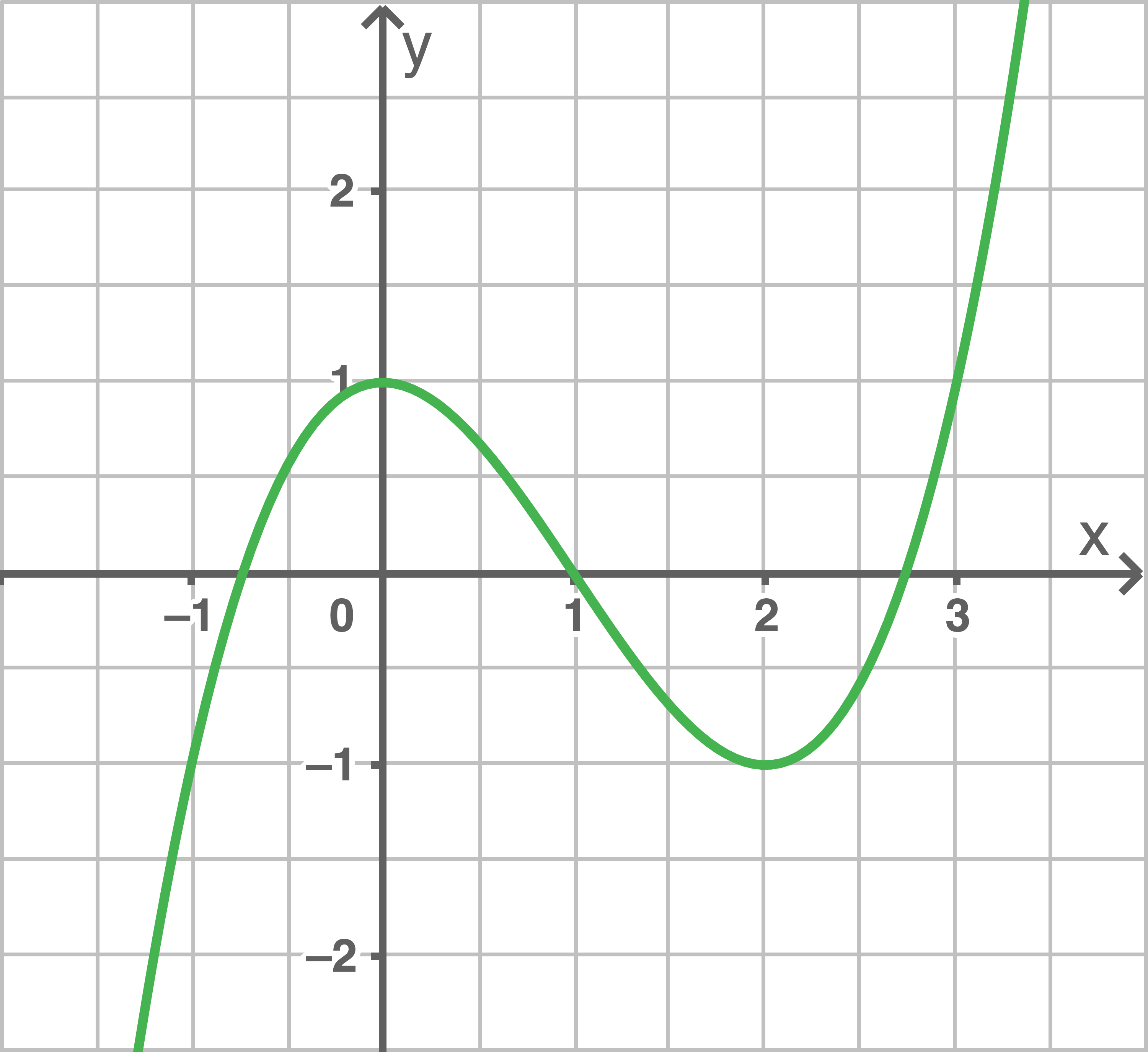
Zeichne jeweils den Graphen der Ableitungsfunktion
a)

b)

c)

d)

Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
b)
c)
d)
e)
f)
2.
a)
Da es sich um eine Funktion zweiten Grades handelt, ist die Ableitungsfunktion eine lineare Funktion.
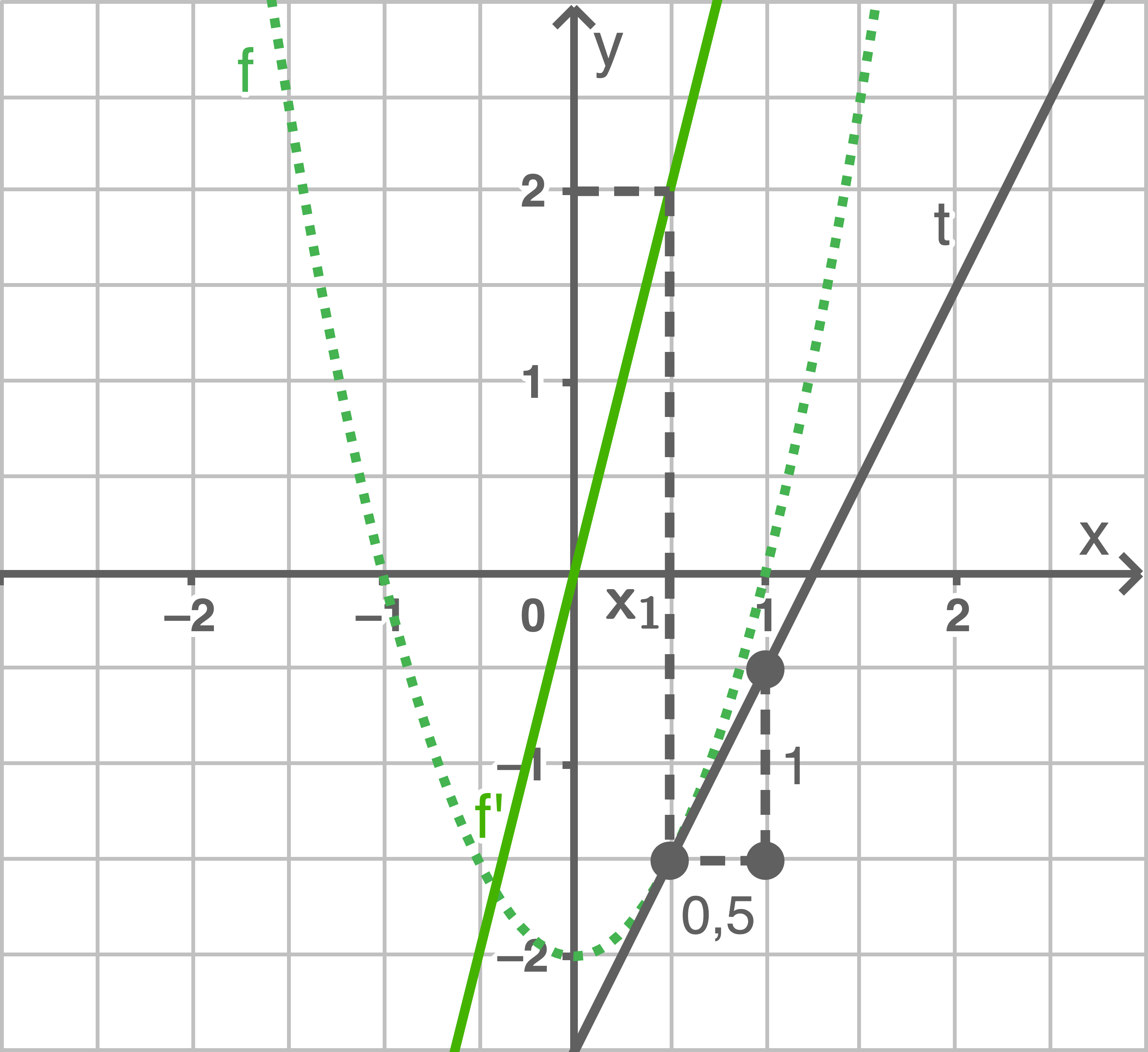
| Graph der Funktion | Graph der Ableitungsfunktion |
|---|---|
| Tiefpunkt bei |
Nullstelle |
| Monoton fallend für |
Verläuft unterhalb der |
| Monoton steigend für |
Verläuft oberhalb der |
| Steigungsdreieck bei |
Funktionswert an der Stelle |

b)
Da es sich um eine Funktion zweiten Grades handelt, ist die Ableitungsfunktion eine lineare Funktion.
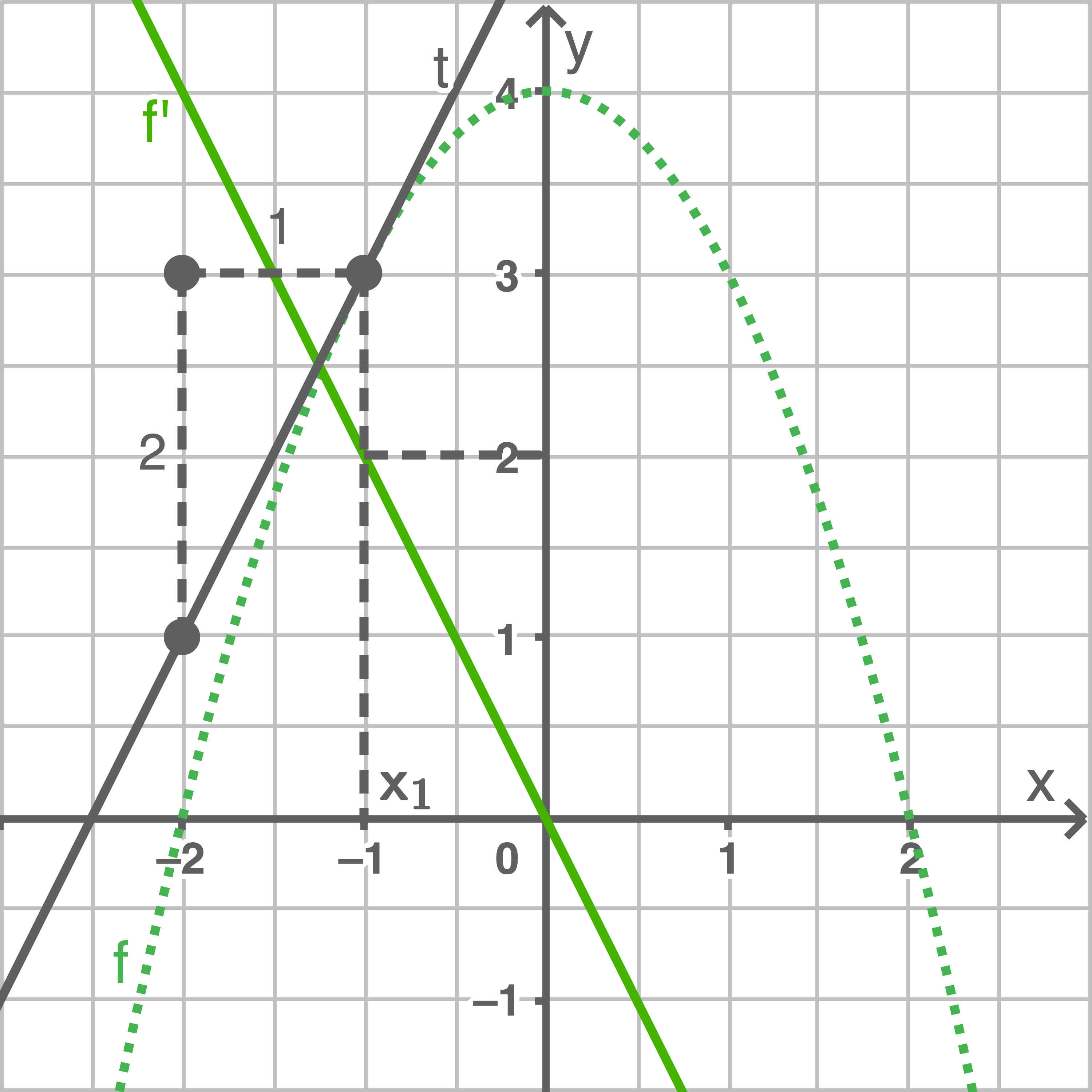
| Graph der Funktion | Graph der Ableitungsfunktion |
|---|---|
| Hochpunkt bei |
Nullstelle |
| Monoton steigend für |
Verläuft oberhalb der |
| Monoton fallend für |
Verläuft unterhalb der |
| Steigungsdreieck bei |
Funktionswert an der Stelle |

c)
Da es sich um eine Funktion dritten Grades handelt, ist die Ableitungsfunktion eine Funktion zweiten Grades.
Steigungsdreieck bei  einzeichnen ergibt die Steigung
einzeichnen ergibt die Steigung  Das lokale Maximum von
Das lokale Maximum von  liegt also an der Stelle
liegt also an der Stelle 
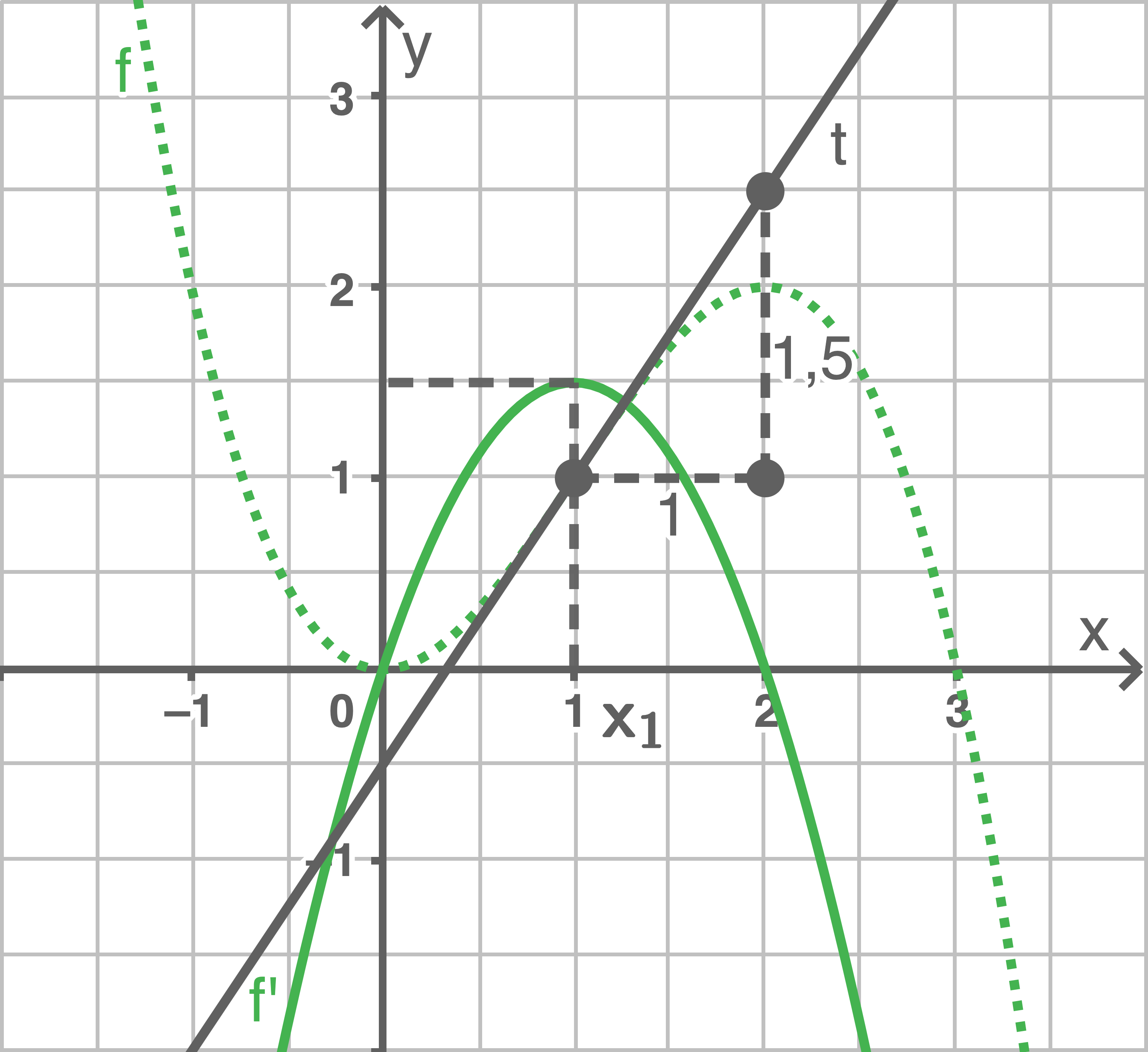
| Graph der Funktion | Graph der Ableitungsfunktion |
|---|---|
| Tiefpunkt bei |
Nullstelle |
| Hochpunkt bei |
Nullstelle |
| Monoton fallend für |
Verläuft unterhalb der |
| Monoton steigend für |
Verläuft oberhalb der |
| Monoton fallend für |
Verläuft unterhalb der |
| Wendepunkt bei |
Lokales Maximum |

d)
Da es sich um eine Funktion dritten Grades handelt, ist die Ableitungsfunktion eine Funktion zweiten Grades.
Steigungsdreieck bei  einzeichnen ergibt die Steigung
einzeichnen ergibt die Steigung  Das lokale Maximum von
Das lokale Maximum von  liegt also an der Stelle
liegt also an der Stelle 
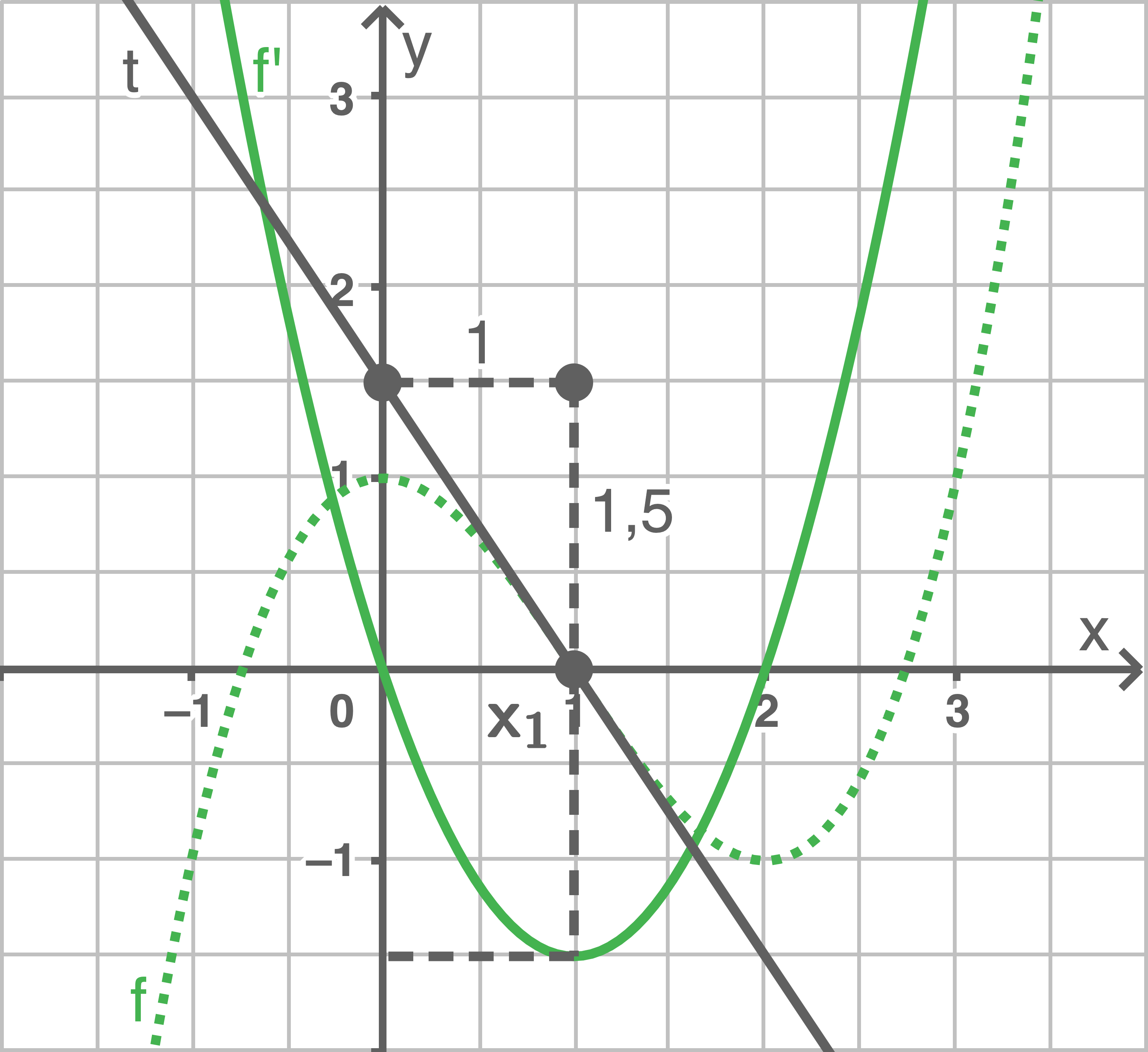
| Graph der Funktion | Graph der Ableitungsfunktion |
|---|---|
| Hochpunkt bei |
Nullstelle |
| Monoton steigend für |
Verläuft oberhalb der |
| Monoton fallend für |
Verläuft unterhalb der |
| Tiefpunkt bei |
Nullstelle |
| Wendepunkt bei |
Lokales Minimum |
