Vermischte Aufgaben

Setze in die Ebene $E:\;\overrightarrow{x}=\left( {\begin{array}{*{20}r} 1 \\ 0 \\ 2 \\ \end{array}} \right)+s\left( {\begin{array}{*{20}r} -5 \\ 2 \\ 3 \\ \end{array}} \right)+t\left( {\begin{array}{*{20}r} 1 \\ 0 \\ 2 \\ \end{array}} \right)$ die Werte $s=2$ und $t=-1$ ein.

Wie lauten die Koordinaten des gesuchten Punktes?

Bestimme zwei weitere Punkte, die auf der Ebene liegen.

Gegeben ist eine Ebenenschar $E_k$ : $x+(k-2)y+(2k+1)z=5-2k$ mit $k\in\mathbb{R}$ .

Die Gerade $h$ geht durch die Punkte $P(0 \mid -4 \mid 1)$ und $Q(3 \mid 2 \mid -2)$ und schneidet $E_1$ .

Berechne den Schnittpunkt $S$ von $h$ und $E_1$ .

Zeige, dass $P$ und $Q$ auf verschiedenen Seiten der Ebene $E_1$ liegen.

Welche der Ebenen $E_k$ enthält den Ursprung? Welche ist zur $z$ -Achse parallel?

Gegeben sind die Geraden

$g:\; \overrightarrow{x}=\left(\begin{array}{r} 1\\ 3\\ 0\\ \end{array}\right)+s\left(\begin{array}{r} 1\\ 0\\ 2\\ \end{array}\right);\;s\in\mathbb{R}$ und $h:\;\overrightarrow{x}=\left(\begin{array}{r} -1\\ 1\\ 2\\ \end{array}\right)+t\left(\begin{array}{r} 2\\ 1\\ -1\\ \end{array}\right)$ $;\;t\in\mathbb{R}$

und der Punkt $A(2 \mid 1 \mid 0)$ .

Bestimme die Lage der Geraden $g$ und $h$ zueinander.

Die Ebene $E$ enthält den Punkt $A$ und die Gerade $g$ .

Bestimme den Schnittpunkt von $E$ und $h$ .

Zeige, dass die beiden Geraden

$g:\;\overrightarrow{x}=\left( {\begin{array}{*{20}r} 0 \\ { 1} \\ 2 \\ \end{array}} \right)+ s\cdot \left( {\begin{array}{*{20}r} 2 \\ { 1} \\ 0 \\ \end{array}} \right);\; s\in\mathbb{R}$ und $h:\;\overrightarrow{x}=\left( {\begin{array}{*{20}r} -2 \\ { 1} \\ 0 \\ \end{array}} \right)+ t\cdot \left( {\begin{array}{*{20}r} -8 \\ { -4} \\ 0 \\ \end{array}} \right);\; t\in\mathbb{R}$

eine Ebene $E$ aufspannen und gib eine Koordinatengleichung von $E$ an.

In einem kartesischen Koordinatensystem sind die Punkte $A(0 \mid 2 \mid 3)$ , $B(1 \mid -2 \mid 6)$ und $C(-4 \mid 2 \mid 15)$ gegeben sowie für jedes $a\in\mathbb{R}$ eine Gerade $g_a$ mit der Gleichung:

$\overrightarrow{x}=\left(\begin{array}{r} -1\\ 2\\ 6\\ \end{array}\right)+s\cdot\left(\begin{array}{r} a\\ 1\\ a-2\\ \end{array}\right)$ ; $\;s\in\mathbb{R}$

Bestimme eine Koordinatengleichung der Ebene $E$ durch $A$ , $B$ und $C$ .

Bestimme die Koordinaten der Schnittpunkte mit der $x$ , $y$ und $z$ -Achse.

Zeichne die Ebene $E$ mithilfe der Spurpunkte in ein Koordinatensystem.

Weise nach, dass keine der Geraden $g_a$ die Ebene $E$ senkrecht schneidet.

Für welchen Wert von $a$ ist die Gerade $g_a$ parallel zur Ebene $E$ ? Ist diese Gerade sogar in $E$ enthalten?

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$E:\;\overrightarrow{x}$ = $\left( {\begin{array}{*{20}r} 1 \\ 0 \\ 2 \\ \end{array}} \right)+s\left( {\begin{array}{*{20}r} -5 \\ 2 \\ 3 \\ \end{array}} \right)+t\left( {\begin{array}{*{20}r} 1 \\ 0 \\ 2 \\ \end{array}} \right)$

Einsetzen von $s=2$ und $t=-1$ liefert:

$E:\;\overrightarrow{x}$ = $\left(\begin{array}{r} 1\\ 0\\ 2\\ \end{array}\right)+2\left(\begin{array}{r} -5\\ 2\\ 3\\ \end{array}\right)-1\cdot\left(\begin{array}{r} 1\\ 0\\ 2\\ \end{array}\right)$ = $\left(\begin{array}{r} -10\\ 4\\ 6\\ \end{array}\right)$ $\;\Rightarrow\;P(-10 \mid 4 \mid 6)$

Ein weiterer Punkt ist $Q(1 \mid 0 \mid 2)$ (Stützvektor der Ebene; $s=t=0$ ).

Setzt man für $s=t=1$ ein, so erhält man einen weiteren Punkt $B$ mit

$E:\;\overrightarrow{OB}$ = $\left(\begin{array}{r} -3\\ 2\\ 7\\ \end{array}\right)$

Vollständige Lösung anzeigen

Der Punkt $B$ hat somit die Koordinaten $B(-3 \mid 2 \mid 7)$ .

Berechnung des Schnittpunktes von $h$ und $E_1$

1.Schritt: Bestimmung der Geraden $h$

$h$ geht durch die Punkte $P(0 \mid -4 \mid 1)$ und $Q(3 \mid 2 \mid -2)$ .

$h$ :

Vollständige Lösung anzeigen

Der Schnittpunkt $S$ ergibt sich durch einsetzen von $h$ in $E_1$ : $x-y+3z=3$ :

$3s-(-4+6s)+3(1-3s)$ = $3$

$\;\Rightarrow\; s$ $=\dfrac{1}{3}$

2.Schritt: $s$ eingesetzt in $h$

$h$ :

Vollständige Lösung anzeigen

Schaut man sich die Strecke $\overline{PQ}$ an, so weiß man, dass diese auf der Geraden $h$ mit

$\overrightarrow{x}$ = $\left(\begin{array}{r} 0\\ -4\\ 1\\ \end{array}\right)+s\cdot\left(\begin{array}{r} 3\\ 6\\ -3\\ \end{array}\right)$ liegt.

Für $s=\dfrac{1}{3}$ gelangen wir zum Schnittpunkt $S$ . Für $s=0$ erhält man den Punkt $P$ und für $s=1$ den Punkt $Q$ . Da $0\lt \frac{1}{3}\lt 1$ gilt, liegt der Punkt $S$ zwischen $P$ und $Q$ . Also liegen die Punkte $P$ und $Q$ auf verschiedenen Seiten von $E_1$ .

Wenn der Ursprung $O(0 \mid 0 \mid 0)$ in $E_k$ : $x+(k-2)y+(2k+1)z$ = $5-2k$ liegen soll, muss $0=5-2k$ $\;\Rightarrow\;$ $k$ = $\dfrac{5}{2}$ gelten. Somit enthält die Ebene $E_{\frac{5}{2}}$ den Ursprung.

Wenn die Ebenen $E_k$ parallel zur $z$ -Achse sein soll, muss für den Normalenvektor $\overrightarrow{n_k}$ dieser Ebene

$\overrightarrow{n_k}\circ\left(\begin{array}{r} 0\\ 0\\ 1\\ \end{array}\right)$ = $0$ = $\left(\begin{array}{r} 1\\ k-2\\ 2k+1\\ \end{array}\right)\circ\left(\begin{array}{r} 0\\ 0\\ 1\\ \end{array}\right)$ = $2k+1$ $\;\Rightarrow\;$ $k$ = $-\dfrac{1}{2}$ gelten.

Die Ebene $E_{-\frac{1}{2}}$ ist somit parallel zur $z$ -Achse.

Die Richtungsvektoren von $g$ und $h$ sind linear unabhängig, da $s \cdot \left(\begin{array}{r} 1\\ 0\\ 2\\ \end{array}\right)\neq\left(\begin{array}{r} 2\\ 1\\ -1\\ \end{array}\right)$ für alle $s\in\mathbb{R}$ gilt.

Somit können die zwei Geraden sich nur noch schneiden oder windschief zueinander liegen.

Gleichsetzen der beiden Geraden liefert:

$\begin{array}{rl} \left(\begin{array}{r} 1\\ 3\\ 0\\ \end{array}\right)+s\left(\begin{array}{r} 1\\ 0\\ 2\\ \end{array}\right)=&... \\[5pt] s\left(\begin{array}{r} 1\\ 0\\ 2\\ \end{array}\right)-t\left(\begin{array}{r} 2\\ 1\\ -1\\ \end{array}\right)=&... \end{array}$

Vollständige Lösung anzeigen

Dies liefert das LGS

$\begin{array}{rll} 1s-2t=&-2&\quad\\[5pt] -t=&-2&\quad\Rightarrow\;t=2\\[5pt] 2s+t=&2&\quad\\ \end{array}$

Setzt man $t=2$ in die erste Gleichung ein ergibt sich $s=2$ . $s$ und $t$ eingesetzt in die dritte Gleichung liefert mit $2\cdot2+2=6\neq2$ eine falsche Aussage.

$\Rightarrow\;$ Die Geraden schneiden sich also nicht, sie liegen daher windschief zueinander.

Um den Schnittpunkt von $E$ und $h$ zu berechnen, wird zunächst eine Parameterform der Ebene bestimmt.

Dabei ist ein Spannvektor der Ebene der Richtungsvektor von $g$ . Der zweite Spannvektor ist der Vektor, der den Punkt $A(2 \mid 1 \mid 0)$ und den Stützvektor der Geraden $g$ verbindet.

$E:\;\overrightarrow{x}$ = $\left(\begin{array}{r} 1\\ 3\\ 0\\ \end{array}\right)+u\left(\begin{array}{r} 1\\ 0\\ 2\\ \end{array}\right)+v\left(\begin{array}{r} 1\\ -2\\ 0\\ \end{array}\right)$

Vollständige Lösung anzeigen

Der Schnittpunkt von $E$ und $h$ ergibt sich durch Gleichsetzen der beiden Gleichungen

$\left(\begin{array}{r} 1\\ 3\\ 0\\ \end{array}\right)+u\left(\begin{array}{r} 1\\ 0\\ 2\\ \end{array}\right)+v\left(\begin{array}{r} 1\\ -2\\ 0\\ \end{array}\right)$ = $\left(\begin{array}{r} -1\\ 1\\ 2\\ \end{array}\right)+s\left(\begin{array}{r} 2\\ 1\\ -1\\ \end{array}\right)$

Es ergibt sich das LGS

$\begin{array}{lrcrcrcrl} Ⅰ&u&+&v&-&...\\[5pt] Ⅱ&&-&2v&-&...\\[5pt] Ⅲ&2u&&&+&...\\[5pt] \hline Ⅰ&u&+&v&-&...\\[5pt] Ⅱ&&-&2v&-&...\\[5pt] Ⅲa&&-&2v&+&...\\[5pt] \hline Ⅰ&u&+&v&-&...\\[5pt] Ⅱ&&-&2v&-&...\\[5pt] Ⅲb&...\\ \end{array}$

Vollständige Lösung anzeigen

Aus $Ⅲb$ folgt: $s=\dfrac{4}{3}$ .

Setzt man $s=\dfrac{4}{3}$ die Geradengleichung von $h$ ein, so ergibt sich für den Schnittpunkt $S$ :

$h:$ $\;\overrightarrow{OS}$ $=\left(\begin{array}{r} -1\\ 1\\ 2\\ \end{array}\right)+\dfrac{4}{3}\left(\begin{array}{r} 2\\ 1\\ -1\\ \end{array}\right)$ $=\left(\begin{array}{r} \frac{5}{3}\\ \frac{7}{3}\\ \frac{2}{3}\\ \end{array}\right)$ $\Rightarrow\;$ $S\left(\frac{5}{3} \mid \;\frac{7}{3} \mid \;\frac{2}{3}\right)$

Die beiden Geraden liegen genau dann in einer Ebene, wenn sie parallel und nicht deckungsgleich sind oder sich schneiden.

Die Geraden sind deckungsgleich, wenn ihre Richtungsvektoren linear abhängig sind und sie unendlich viele Punkte gemeinsam haben.

Die Geraden sind parallel, wenn ihre Richtungsvektoren linear abhängig sind und sie keine Punkte gemeinsam haben.

1.Schritt: Gegenseitige Lage der Geraden

$g$ und $h$ haben linear abhängige Richtungsvektoren:

$\left( {\begin{array}{*{20}r} 2 \\ { 1} \\ 0 \\ \end{array}} \right)$ = $-\dfrac{1}{4}\left( {\begin{array}{*{20}r} -8 \\ { -4} \\ 0 \\ \end{array}} \right)$

Nun muss man noch überprüfen, ob die Geraden gemeinsame Punkte haben. Das überprüft man z.B., indem man den Stützvektor $\overrightarrow{OP}$ = $\left( {\begin{array}{*{20}r} 0 \\ { 1} \\ 2 \\ \end{array}} \right)$ $\left(P(0 \mid 1 \mid 2)\right)$ in $h$ einsetzt.

$\left( {\begin{array}{*{20}r} 0 \\ { 1} \\ 2 \\ \end{array}} \right)$ = $\left( {\begin{array}{*{20}r} -2 \\ { 1} \\ 0 \\ \end{array}} \right)+ t\cdot \left( {\begin{array}{*{20}r} -8 \\ { -4} \\ 0 \\ \end{array}} \right)$

Dies liefert das LGS:

$\begin{array}{rll} 0=&-2-8t&\quad\\[5pt] 1=&1-4t&\\[5pt] 2=&0+0t&\\ \end{array}$

Die erste Gleichung hat die Lösungen $t=-\dfrac{1}{4}$ , die zweite Gleichung hat die Lösungen $t=0$ .

Damit liegt der Punkt $P$ nicht auf der Geraden $h$ .

Die Geraden $g$ und $h$ sind also parallel und liegen somit in einer Ebene $E$ .

2.Schritt: Bestimmung der Koordinatengleichung von $E$

Einen Richtungsvektor der Geraden kann man als Spannvektor der Ebene verwenden: $\left(\begin{array}{r} 2\\ 1\\ 0\\ \end{array}\right)$ .

Der andere Spannvektor ergibt sich aus dem Verbindungsvektor der beiden Stützpunkte:

$\left( {\begin{array}{*{20}r} 0 \\ { 1} \\ 2 \\ \end{array}} \right)-\left( {\begin{array}{*{20}r} -2 \\ { 1} \\ 0 \\ \end{array}} \right)$ = $\left( {\begin{array}{*{20}r} 2 \\ { 0} \\ 2 \\ \end{array}} \right)$

3.Schritt: Bestimmung des Normalenvektors $\overrightarrow{n}$

$\overrightarrow{n}\cdot \left( {\begin{array}{*{20}r} 2 \\ { 1} \\ 0 \\ \end{array}} \right)=0$ ; $\overrightarrow{n}\cdot \left( {\begin{array}{*{20}r} 2 \\ { 0} \\ 2 \\ \end{array}} \right)=0$

$\begin{array}{rll} 2n_1+n_2=&0&\quad\Rightarrow\; n_1=-\frac{1}{2}n_2\\[5pt] 2n_1+2n_3=&0&\quad\Rightarrow\; n_1=-n_3\\ \end{array}$

Eine mögliche Lösung ist:

$n_1=1$ , $n_2=-2$ , $n_3=-1$ , also $\overrightarrow{n}$ = $\left( {\begin{array}{*{20}r} 1 \\ { -2} \\ -1 \\ \end{array}} \right)$ .

Setzt man nun in die vorläufige Koordinatengleichung $x_1-2x_2-x_3=d$ den Punkt $P(0 \mid 1 \mid 2)$ ein, so ergibt sich $d=-4$ und man erhält die Koordinatengleichung der Ebene:

$E:\;x_1-2x_2-x_3=-4$

1.Schritt: Bestimmung einer Koordinatengleichung von $E$ :

Gegeben sind die Punkte $A(0 \mid 2 \mid 3)$ , $B(1 \mid -2 \mid 6)$ und $C(-4 \mid 2 \mid 15)$ :

$\begin{array}{rll} E: \end{array}$

Vollständige Lösung anzeigen

2.Schritt: Normalenvektor von E:

$\begin{array}{lrlrl} Ⅰ\;\;&\overrightarrow{n}\cdot\overrightarrow{AB}=0\\[5pt] Ⅱ\;\;&\overrightarrow{n}\cdot\overrightarrow{AC}=0\\ \end{array}$

Vollständige Lösung anzeigen

Für $n_1=6$ ergibt sich $n_3=2$ und $n_2=3$ (eingesetzt in Ⅰ):

$E$ : $6x+3y+2z=d$

$A(0 \mid 2 \mid 3)$ eingesetzt in $E$ liefert:

$E$ : $6x+3y+2z=12$

Bestimmung der Schnittpunkte mit den Achsen

Schnittpunkt von $E$ mit der

$x$ -Achse: $y=z=0$

$y$ -Achse: $x=z=0$

$z$ -Achse: $x=y=0$

Vollständige Lösung anzeigen

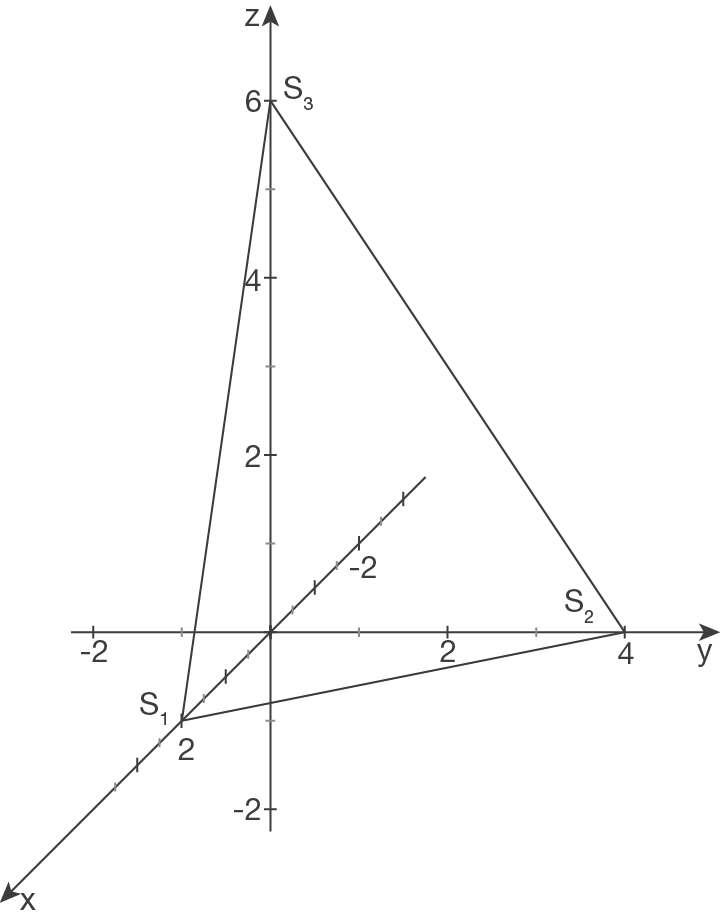
3D-Koordinatensystem mit Linien und Punkten in den Achsen x, y und z.

Die Gerade $\overrightarrow{x}$ $=\left(\begin{array}{r} -1\\ 2\\ 6\\ \end{array}\right)+s\cdot\left(\begin{array}{r} a\\ 1\\ a-2\\ \end{array}\right)$ schneidet $E$ rechtwinklig,

wenn der Normalenvektor der Ebene $E$ und der Richtungsvektor der Gerade für ein $a\in\mathbb{R}$ linear abhängig sind.

$\left(\begin{array}{r} a\\ 1\\ a-2\\ \end{array}\right)$ $=k\cdot\left(\begin{array}{r} 6\\ 3\\ 2\\ \end{array}\right)$

Dies liefert das LGS:

$\begin{array}{rll} a=&6k&\quad\Rightarrow a=2\\[5pt] 1=&3k&\quad\Rightarrow k=\dfrac{1}{3}\\ a=&2k+2&\quad\Rightarrow a=\dfrac{8}{3}\\ \end{array}$

Das Gleichungssystem ist nicht lösbar. Es gibt somit keine Gerade $g_a$ die orthogonal zu $E$ steht.

Eine Gerade $g_a$ ist parallel zu $E$ , wenn der Richtungsvektor der Geraden und der Normalenvektor von $E$ senkrecht zueinander stehen.

$\left(\begin{array}{r} a\\ 1\\ a-2\\ \end{array}\right)\circ\left(\begin{array}{r} 6\\ 3\\ 2\\ \end{array}\right)$ $=6a+3+2a-4$ = $8a-1=0$ $\;\Rightarrow\;$ $a=\dfrac{1}{8}$

Die Gerade $g_{\frac{1}{8}}$ : $\overrightarrow{x}$ $=\left(\begin{array}{r} -1\\ 2\\ 6\\ \end{array}\right)+s\cdot\left(\begin{array}{r} \frac{1}{8}\\ 1\\ -\frac{15}{8}\\ \end{array}\right)$ $=\left(\begin{array}{r} -1\\ 2\\ 6\\ \end{array}\right)+s\cdot\left(\begin{array}{r} 1\\ 8\\ -15\\ \end{array}\right)$ liegt nun entweder in oder parallel zu $E$ .

Prüfen, ob $g$ in $E$ liegt:

$g_{\frac{1}{8}}$ eingesetzt in $E$ liefert:

$6(-1+s)+3(2+8s)+2(6-15s)$ $=12$ $\;\Longleftrightarrow\;$ $12=12$

Damit ist gezeigt, dass für alle $s$ die Gerade $g_{\frac{1}{8}}$ in $E$ enthalten ist.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?