Parameterform
Eine Ebene im dreidimensionalen Raum kann durch drei verschiedene Punkte, die nicht alle auf einer Geraden liegen, vollständig definiert werden: Sind beispielsweise drei Punkte  ,
,  und
und  gegeben, die in der Ebene
gegeben, die in der Ebene  liegen sollen, so kann die Gleichung dieser Ebene in Parameterform wie folgt angegeben werden:
liegen sollen, so kann die Gleichung dieser Ebene in Parameterform wie folgt angegeben werden:
 =
= Hierbei versteht man unter
Hierbei versteht man unter
 ,
,  und
und  .
.
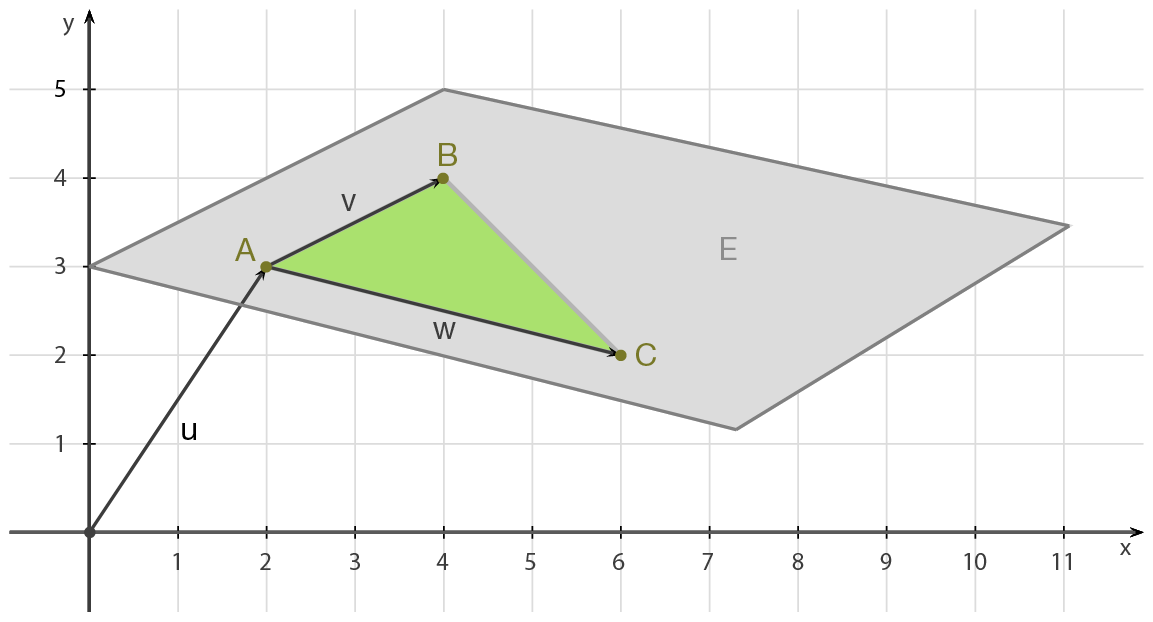
Zuerst legen wir fest, dass der Vektor Stützvektor und
Stützvektor und  ,
,  Spannvektoren sein sollen. Du kannst auch
Spannvektoren sein sollen. Du kannst auch  oder
oder  als Stützvektor wählen, dadurch erhältst du dieselbe Ebene im Raum.
als Stützvektor wählen, dadurch erhältst du dieselbe Ebene im Raum.



Durch Einsetzen erhältst du die Ebenengleichung von in Parameterform:
in Parameterform:
den Stützvektor der Ebene
, der die Verschiebung im Raum angibt
,
die Spannvektoren der Ebene
, die die Ebene aufspannen
,
reelle Zahlen, für die die Spannvektoren beliebig lang bzw. kurz werden können und somit alle Punkte auf der Ebene erreicht werden können.

Beispiel
Gegeben sind die PunkteZuerst legen wir fest, dass der Vektor
Durch Einsetzen erhältst du die Ebenengleichung von
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
Gesucht ist eine Ebenengleichung in Parameterform
 .
Eine mögliche Parametergleichung von
.
Eine mögliche Parametergleichung von  lautet:
lautet:
 ,
,  ,
,  :
Als Stützvektor
:
Als Stützvektor  kann man z.B. den Ortsvektor
kann man z.B. den Ortsvektor  von
von  verwenden.
Eingesetzt in die Ebenengleichung erhält man
verwenden.
Eingesetzt in die Ebenengleichung erhält man

 ,
,  ,
,  :
Als Stützvektor
:
Als Stützvektor  kann man z.B. den Ortsvektor
kann man z.B. den Ortsvektor  von
von  verwenden.
Multipliziert man
verwenden.
Multipliziert man  noch mit
noch mit  erhält man die Ebenengleichung
erhält man die Ebenengleichung

a)
b)
2.
Um zu überprüfen, ob  in
in  liegt, setzt man
liegt, setzt man  in
in  ein.
ein.
 ;
;
 :
: =
=
Nun stellt man ein lineares Gleichungssystem oder eine Matrix auf:![\( \begin{array}{lrcrcrl}
Ⅰ&-1s&+&3t&=&-5&\\[5pt]
Ⅱ&2s&+&2t&=&2&\\[5pt]
Ⅲ&1s&+&0\cdot t&=&2&\\
\end{array}\)](https://mathjax.schullv.de/ff8f987af1047127030fd53b070188295031233192639dc29674ff6197b9894f?color=5a5a5a) Aus Ⅲ folgt
Aus Ⅲ folgt  .
.  in Ⅱ liefert uns:
in Ⅱ liefert uns:
![\( \begin{array}[t]{rll}
4+2t=&2&\quad\mid-4\\[5pt]
2t=&-2&\quad\mid:2\\[5pt]
t=&-1&\quad\\
\end{array}\)](https://mathjax.schullv.de/f562791e9ea3369a64f17684440ae6c2ae7a4d16352a939447a45a997309e2dd?color=5a5a5a)
 und
und  in Ⅰ eingesetzt:
in Ⅰ eingesetzt:
 =
= Somit sind alle drei Gleichungen erfüllt, also liegt der Punkt
Somit sind alle drei Gleichungen erfüllt, also liegt der Punkt  in der Ebene
in der Ebene  .
.
 ;
;
 :
: =
=
Nun stellt man ein lineares Gleichungssystem oder eine Matrix auf:![\( \begin{array}{lrcrcrl}
Ⅰ&1s&+&0t&=&3&\\[5pt]
Ⅱ&2s&+&t&=&1&\\[5pt]
Ⅲ&0s&+&t&=&1&\quad \\
\end{array}\)](https://mathjax.schullv.de/b5d1c73ccdfd0e685b51f0b9fa651ee6da2bfce4940ceec1287a07b108573133?color=5a5a5a) Aus Ⅰ folgt
Aus Ⅰ folgt  . Aus Ⅲ folgt
. Aus Ⅲ folgt 
 und
und  in Ⅱ liefert uns:
in Ⅱ liefert uns:

 falsche Aussage
Somit ist das LGS nicht lösbar, also liegt der Punkt
falsche Aussage
Somit ist das LGS nicht lösbar, also liegt der Punkt  nicht in der Ebene
nicht in der Ebene  .
.
a)
Nun stellt man ein lineares Gleichungssystem oder eine Matrix auf:
b)
Nun stellt man ein lineares Gleichungssystem oder eine Matrix auf:
3.
Um zu überprüfen für welches  ,
,  in
in  liegt, setzt man zunächst
liegt, setzt man zunächst  in
in  ein.
ein.
 ;
;
 :
: =
=
Nun stellt man ein LGS oder eine Matrix auf:![\(\begin{array}{lrcrcrl}
Ⅰ&2s&-&t&=&3&\\[5pt]
Ⅱ&s&+&2t&=&r-2&\\[5pt]
Ⅲ&0&+&3t&=&9&\\
\end{array}\)](https://mathjax.schullv.de/a7de30815c5b315d9ccbd4a4970fb3e6632fc4a0d7cdfc176c7e63899048dbbe?color=5a5a5a) Aus Ⅲ folgt
Aus Ⅲ folgt  .
.  in Ⅰ liefert uns:
in Ⅰ liefert uns:
![\(\begin{array}[t]{rll}
2s-3=&3&\quad\mid+3\\[5pt]
2s=&6&\quad\mid:2\\[5pt]
s=&3&\quad\\
\end{array}\)](https://mathjax.schullv.de/bff488129765ea2debe4df4ca4ee8b30b703daa2ece233571585e19de997f7c5?color=5a5a5a)
 und
und  in Ⅱ eingesetzt:
in Ⅱ eingesetzt:
![\(\begin{array}[t]{rll}
3\cdot 1+3\cdot2=&r-2&\quad\mid+2\\[5pt]
11=&r&\\
\end{array}\)](https://mathjax.schullv.de/86bb78d9ff0cded91a93b62c1a95bffbac942fb30b6d8d2b189834c4986c79f7?color=5a5a5a) Somit sind für
Somit sind für  alle drei Gleichungen erfüllt. Also liegt für
alle drei Gleichungen erfüllt. Also liegt für  der Punkt
der Punkt  in der Ebene
in der Ebene  .
.
 ;
;
 :
: =
=
Nun stellt man ein LGS oder eine Matrix auf:![\(\begin{array}{lrcrcrl}
Ⅰ&1s&+&1t&=&-1&\\[5pt]
Ⅱ&r\cdot s&+&2t&=&2&\\[5pt]
Ⅲ&0\cdot s&+&2t&=&-2&\quad \\
\end{array}\)](https://mathjax.schullv.de/2a00558e81b6a52b3f0f7972ba6ce5ae9ad10f5e659186925d882ffbe20038e7?color=5a5a5a) Aus Ⅲ folgt
Aus Ⅲ folgt  .
.  in Ⅰ liefert uns:
in Ⅰ liefert uns:
![\(\begin{array}[t]{rll}
s-1=&-1&\quad\mid+1\\[5pt]
s=&0&\quad\\
\end{array}\)](https://mathjax.schullv.de/13883cc426a38eeaec2ceb5b89a8e72313d04dae17ee8cd4fc744c026ccb0b4e?color=5a5a5a)
 und
und  in Ⅱ eingesetzt:
in Ⅱ eingesetzt:  Somit ist das LGS nicht lösbar. Damit liegt für alle
Somit ist das LGS nicht lösbar. Damit liegt für alle  der Punkt
der Punkt  nicht in der Ebene
nicht in der Ebene  .
.
a)
Nun stellt man ein LGS oder eine Matrix auf:
b)
Nun stellt man ein LGS oder eine Matrix auf: