Wurzelfunktionen
Wenn du den Graphen einer Quadratwurzelfunktion zeichnen willst, beachte folgende Punkte:
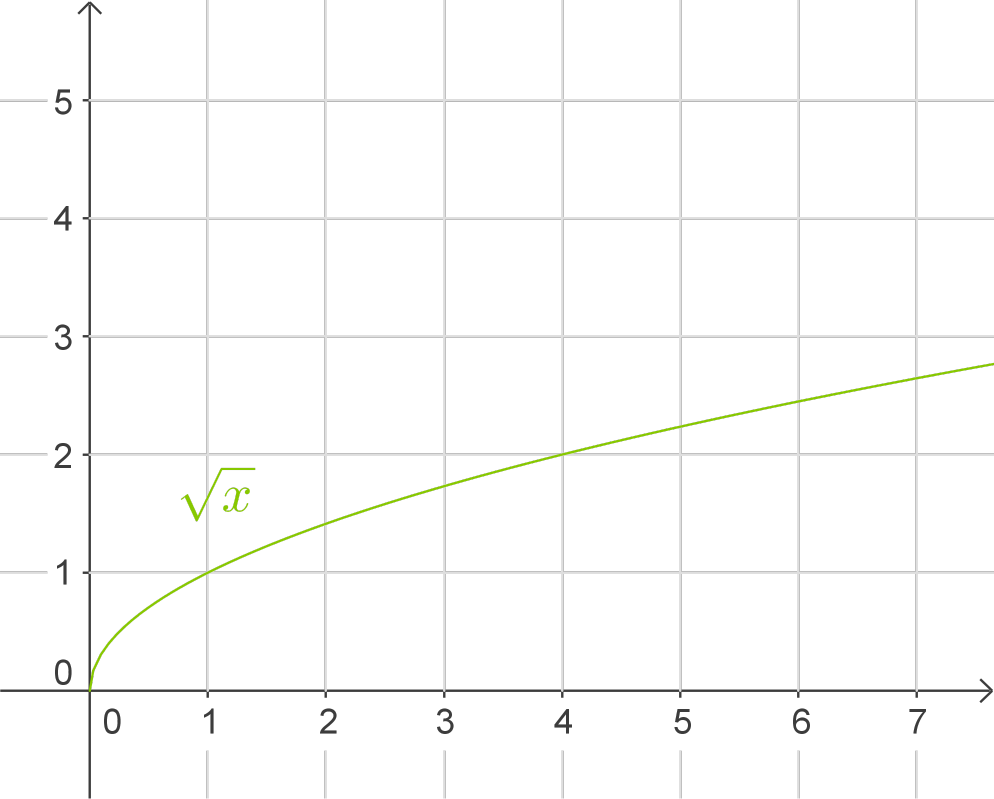
- Die Quadratwurzelfunktion
ist nur für positive Zahlen definiert. Ihr Graph beginnt im Punkt
und ist streng monoton steigend.
- Der Graph wird entlang der
-Achse nach oben verschoben, wenn eine Konstante
zu
addiert wird, nach unten, wenn die Konstante
subtrahiert wird:
. Verschiebungen nach rechts finden statt, wenn unter der Wurzel eine Kostante
subtrahiert wird, nach links, wenn die Konstante
addiert wird:
- Wird die Funktion mit einem Faktor
multipliziert, streckst du den Graph entlang der
-Achse, ist der Faktor
, stauchst du den Graph entlang der
-Achse:
- Der Graph wird an der
-Achse gespiegelt, wenn ein negatives Vorzeichen vor die Funktion geschrieben wurde:
. Du spiegelst die Funktion an der
-Achse, wenn unter der Wurzel ein negatives Vorzeichen steht
. In diesem Fall dürfen für
dann nur negative Werte eingesetzt werden.
1.
Skizziere die Schaubilder folgender Funktionen und bestimme den Definitionsbereich.






a)
b)
c)
d)
e)
f)
2.
Skizziere das Schaubild der Funktion und beschreibe, wie es aus dem Schaubild der Wurzelfunktion hervorgeht.






a)
b)
c)
d)
e)
f)
3.
Verschiebe das Schaubild der angegebenen Funktion wie gefordert und gib die Funktionsgleichung der neuen Funktion an.
 Verschiebung um 1 LE in positive x-Richtung („nach rechts“) und um 3 LE in positive y-Richtung („nach oben“)
Verschiebung um 1 LE in positive x-Richtung („nach rechts“) und um 3 LE in positive y-Richtung („nach oben“)
 Verschiebung um 3 LE in negative x-Richtung („nach links“) und um 4 LE in positive y-Richtung („nach oben“)
Verschiebung um 3 LE in negative x-Richtung („nach links“) und um 4 LE in positive y-Richtung („nach oben“)
 Verschiebung um 2 LE in negative x-Richtung („nach links“) und um 4 LE in negative y-Richtung („nach unten“)
Verschiebung um 2 LE in negative x-Richtung („nach links“) und um 4 LE in negative y-Richtung („nach unten“)
 Verschiebung um 2 LE in positive y-Richtung („nach oben“) und anschließende Spiegelung an der x-Achse
Verschiebung um 2 LE in positive y-Richtung („nach oben“) und anschließende Spiegelung an der x-Achse
 Verschiebung um 3 LE in positive x-Richtung („nach rechts“) und anschließende Spiegelung an der y-Achse
Verschiebung um 3 LE in positive x-Richtung („nach rechts“) und anschließende Spiegelung an der y-Achse
 Verschiebung um 1 LE in positive y-Richtung („nach oben“) und um 3 LE in negative x-Richtung („nach links“)
Verschiebung um 1 LE in positive y-Richtung („nach oben“) und um 3 LE in negative x-Richtung („nach links“)
a)
b)
c)
d)
e)
f)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
Die Wurzelfunktion  ist für alle
ist für alle  definiert. Der Ausdruck, der „unter“ der Wurzel steht, wird Radikand genannt. Der Definitionsbereich besteht also genau aus den Zahlen, für die der Wert unter der Wurzel nicht kleiner als Null wird.
definiert. Der Ausdruck, der „unter“ der Wurzel steht, wird Radikand genannt. Der Definitionsbereich besteht also genau aus den Zahlen, für die der Wert unter der Wurzel nicht kleiner als Null wird.
Das Schaubild einer Funktion mit
mit  entsteht aus dem Schaubild der Wurzelfunktion
entsteht aus dem Schaubild der Wurzelfunktion  durch Streckung bzw. Stauchung in
durch Streckung bzw. Stauchung in  -Richtung um Faktor
-Richtung um Faktor  , Streckung bzw. Stauchung in
, Streckung bzw. Stauchung in  -Richtung um Faktor
-Richtung um Faktor  , Verschiebung in
, Verschiebung in  -Richtung um
-Richtung um  LE und Verschiebung in
LE und Verschiebung in  -Richtung um
-Richtung um  LE.
LE.
Das Schaubild einer Funktion
1.
Schaubilder skizzieren und Definitionsbereiche angeben

Definitionsbereich bestimmen
Untersuche, für welche Werte von der Radikand größer oder gleich Null ist:
der Radikand größer oder gleich Null ist:
![\( \begin{array}[t]{rll}
x+1& \geq &0 &\quad \scriptsize \mid\; -1 \\[5pt]
x&\geq& -1
\end{array}\)](https://www.schullv.de/resources/formulas/4402ad01fdbaa7a5c83dc135381977da0fc42e0ebc0128d1c0b035af139f58fd_light.svg) Damit erhältst du den Definitionsbereich
Damit erhältst du den Definitionsbereich  bzw.
bzw.  .
.
Skizze
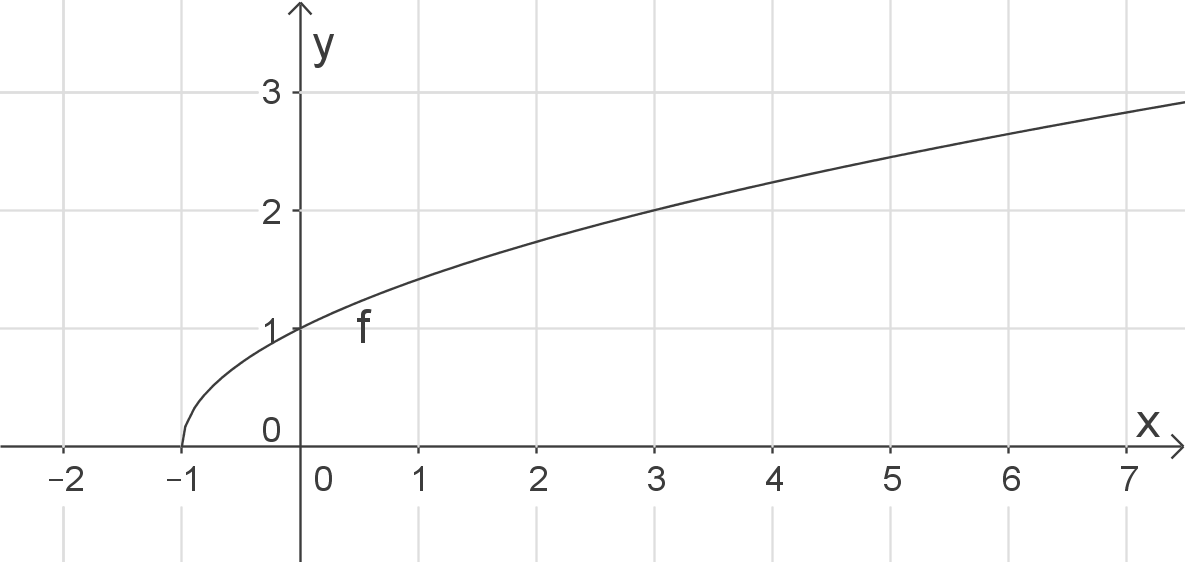

Definitionsbereich bestimmen
![\( \begin{array}[t]{rll}
x-1& \geq &0 &\quad \scriptsize \mid\; +1\\[5pt]
x&\geq& 1
\end{array}\)](https://www.schullv.de/resources/formulas/4afba240c834125a94aef363d673ece0cdd10d30e513ee11f5aafb5908ef22b1_light.svg) Damit erhältst du den Definitionsbereich
Damit erhältst du den Definitionsbereich  bzw.
bzw.  .
.
Skizze
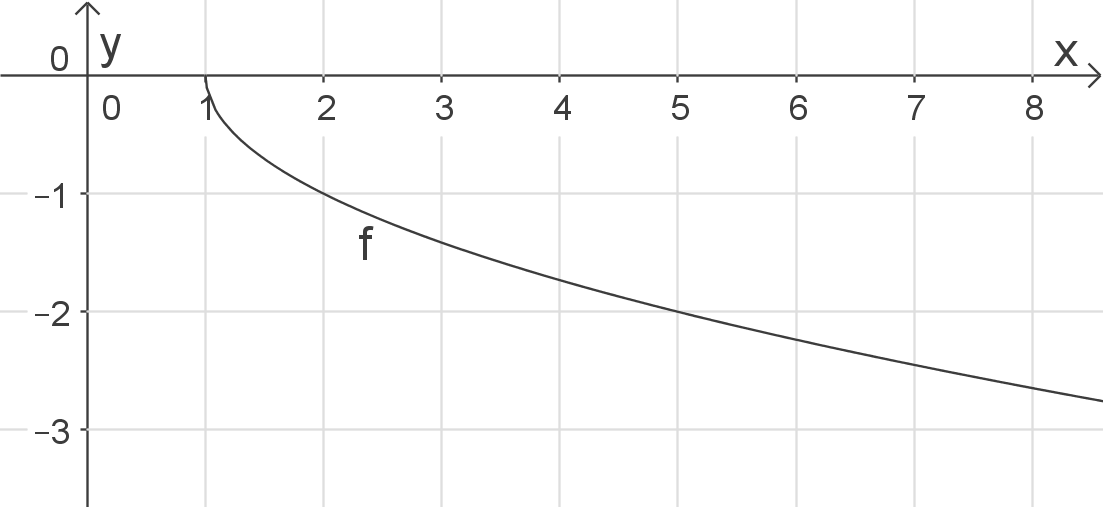

Definitionsbereich bestimmen
![\( \begin{array}[t]{rll}
x+3&\geq&0 &\quad \scriptsize \mid\; -3\\[5pt]
x&\geq& -3
\end{array}\)](https://www.schullv.de/resources/formulas/0ade237639469e8f965178a3cad56375b3253600674728407814b4c64d3a777f_light.svg) Damit erhältst du den Definitionsbereich
Damit erhältst du den Definitionsbereich  bzw.
bzw.  .
.
Skizze
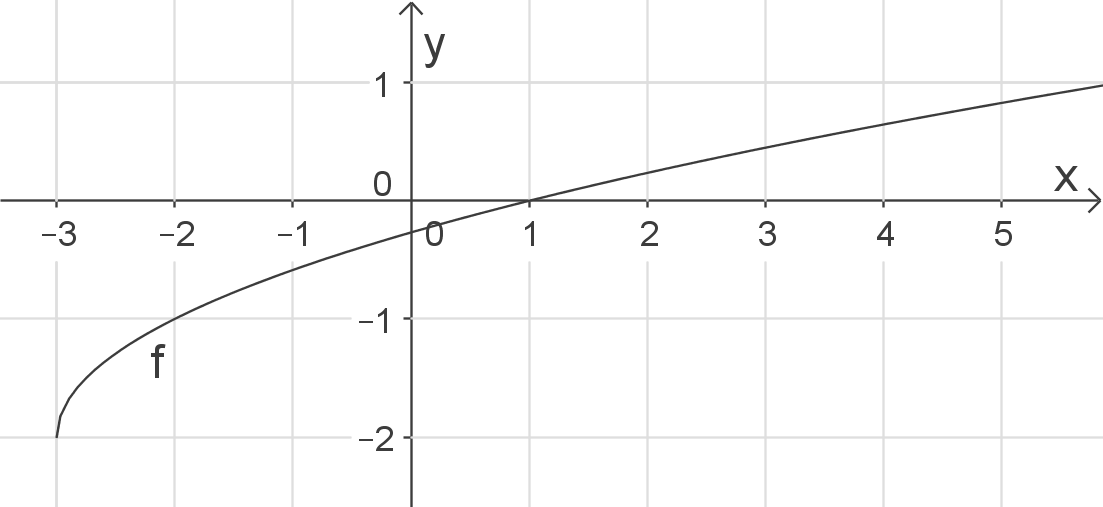

Definitionsbereich bestimmen
![\( \begin{array}[t]{rll}
2x-1&\geq& 0 &\quad \scriptsize \mid\; +1\\[5pt]
2x&\geq& 1 &\quad \scriptsize \mid\; :2\\[5pt]
x&\geq&\frac{1}{2}
\end{array}\)](https://www.schullv.de/resources/formulas/fadabde1ae280d70feb76a7d9dbde3838d7ae80d09d4664afc9ec478266c1586_light.svg) Damit erhältst du den Definitionsbereich
Damit erhältst du den Definitionsbereich  bzw.
bzw.  .
.
Skizze
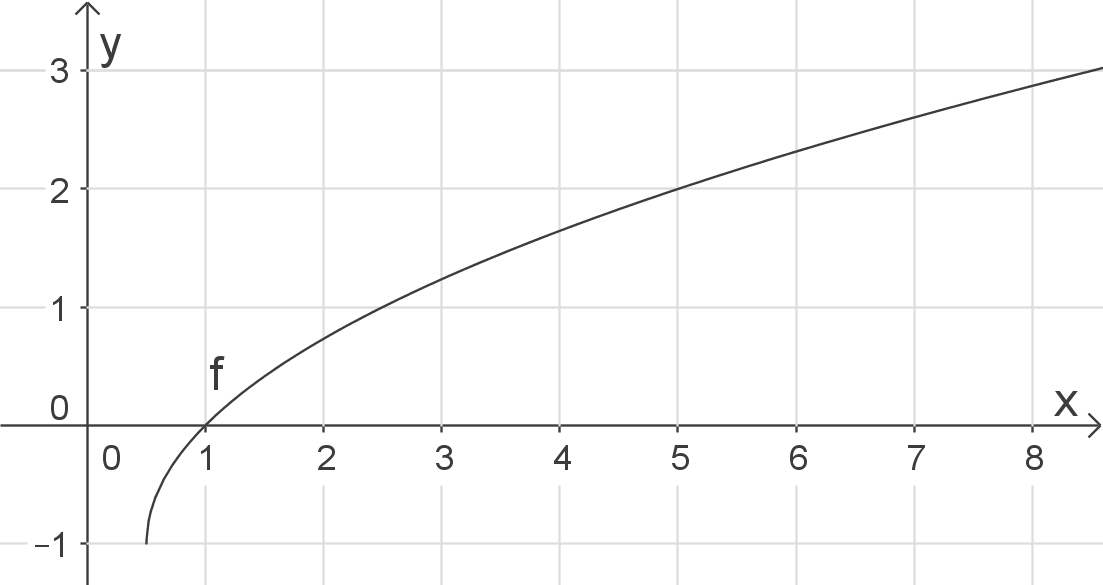

Definitionsbereich bestimmen
 Damit erhältst du den Definitionsbereich
Damit erhältst du den Definitionsbereich  bzw.
bzw.  .
.
Skizze
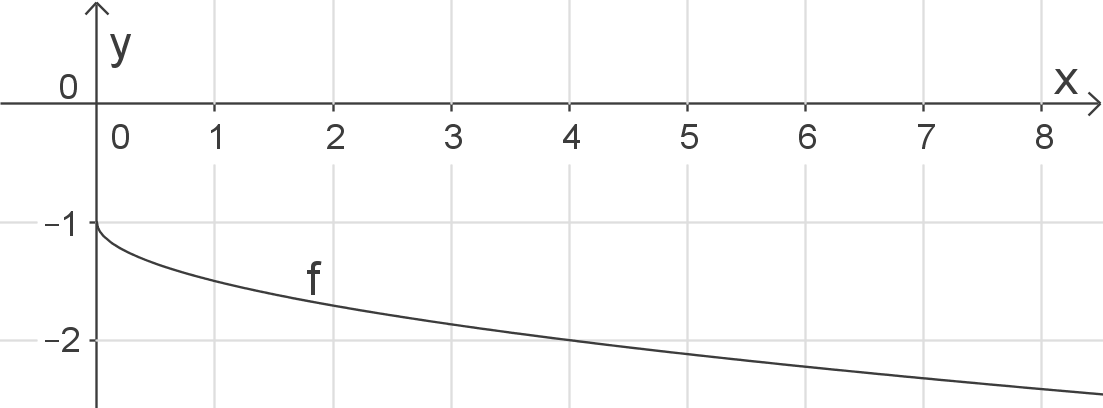

Definitionsbereich bestimmen
![\( \begin{array}[t]{rll}
2x&\geq& 0 &\quad \scriptsize \mid\; :2\\[5pt]
x&\geq& 0
\end{array}\)](https://www.schullv.de/resources/formulas/fc2fbf094df6843a3c6459868d38c53c77cb68c184db3e035df10420f04a3aed_light.svg) Damit erhältst du den Definitionsbereich
Damit erhältst du den Definitionsbereich  bzw.
bzw.  .
.
Skizze
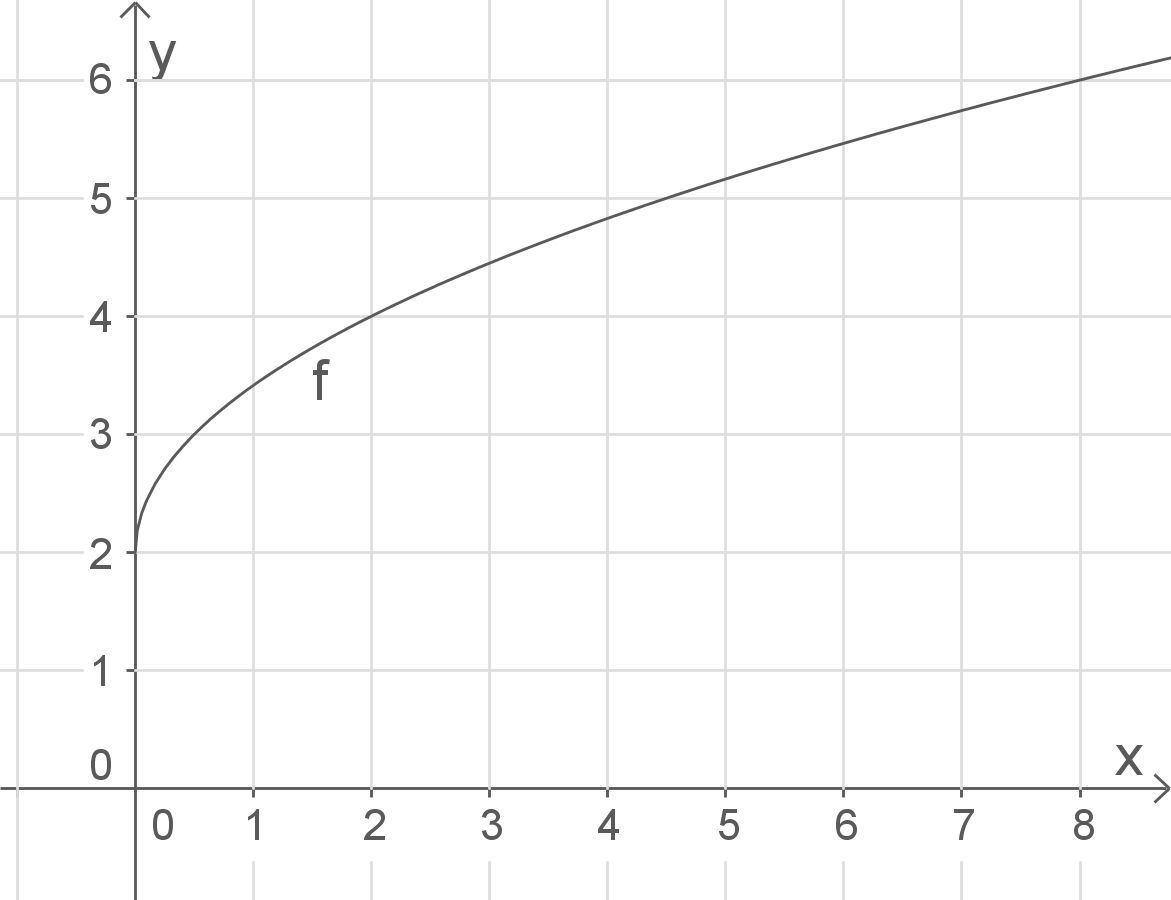
a)
Definitionsbereich bestimmen
Untersuche, für welche Werte von
Skizze

b)
Definitionsbereich bestimmen
Skizze

c)
Definitionsbereich bestimmen
Skizze

d)
Definitionsbereich bestimmen
Skizze

e)
Definitionsbereich bestimmen
Skizze

f)
Definitionsbereich bestimmen
Skizze

2.
Schaubilder skizzieren und herleiten
 Skizze
Skizze
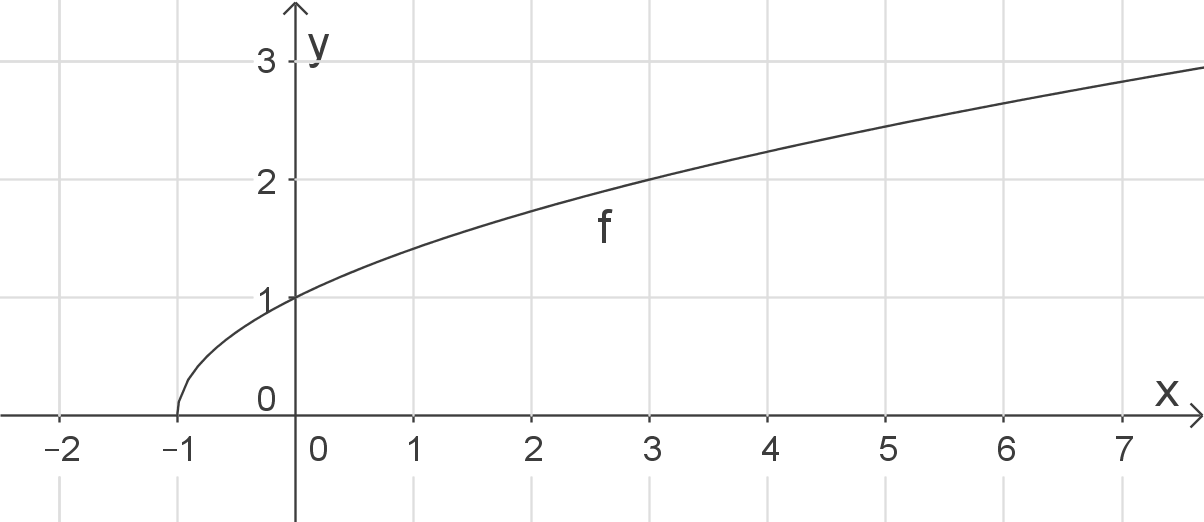 Schaubild herleiten
Das Schaubild von
Schaubild herleiten
Das Schaubild von  geht aus dem Schaubild der Wurzelfunktion durch Verschiebung um 1 LE in negative
geht aus dem Schaubild der Wurzelfunktion durch Verschiebung um 1 LE in negative  -Richtung („nach links“) hervor.
-Richtung („nach links“) hervor.
 Skizze
Skizze
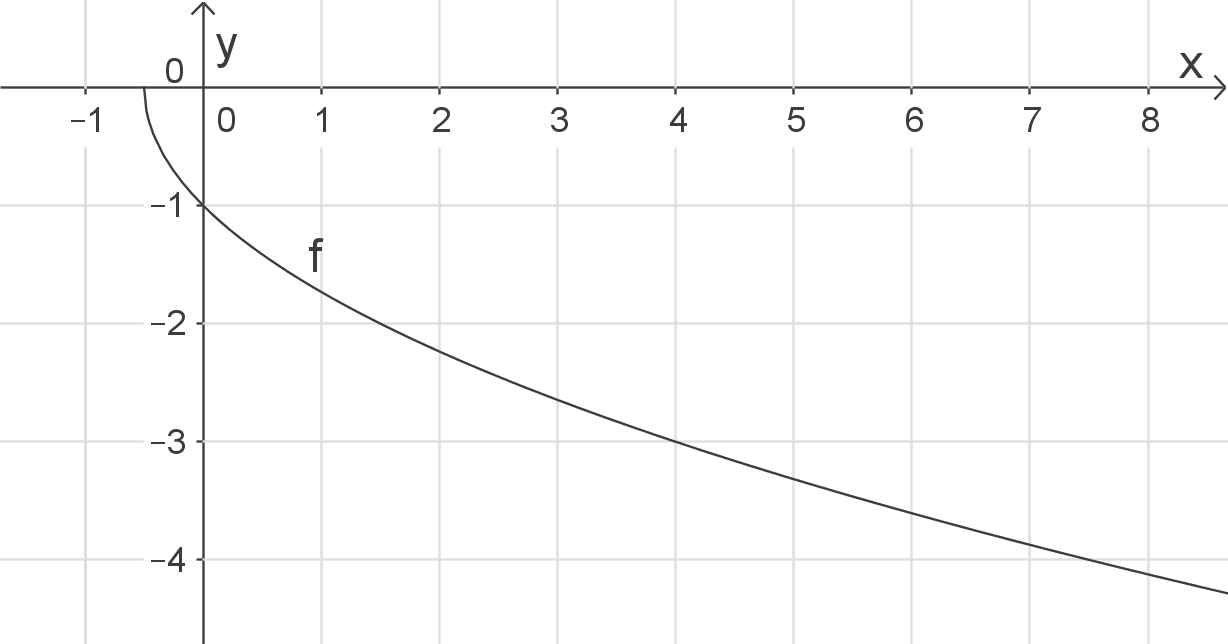 Schaubild herleiten
Das Schaubild von
Schaubild herleiten
Das Schaubild von  geht aus dem Schaubild der Wurzelfunktion hervor durch Spiegelung an der
geht aus dem Schaubild der Wurzelfunktion hervor durch Spiegelung an der  -Achse, Stauchung in
-Achse, Stauchung in  -Richtung um Faktor 2 und Verschiebung in negative
-Richtung um Faktor 2 und Verschiebung in negative  -Richtung („nach links“) um 0,5 LE.
-Richtung („nach links“) um 0,5 LE.
 Skizze
Skizze
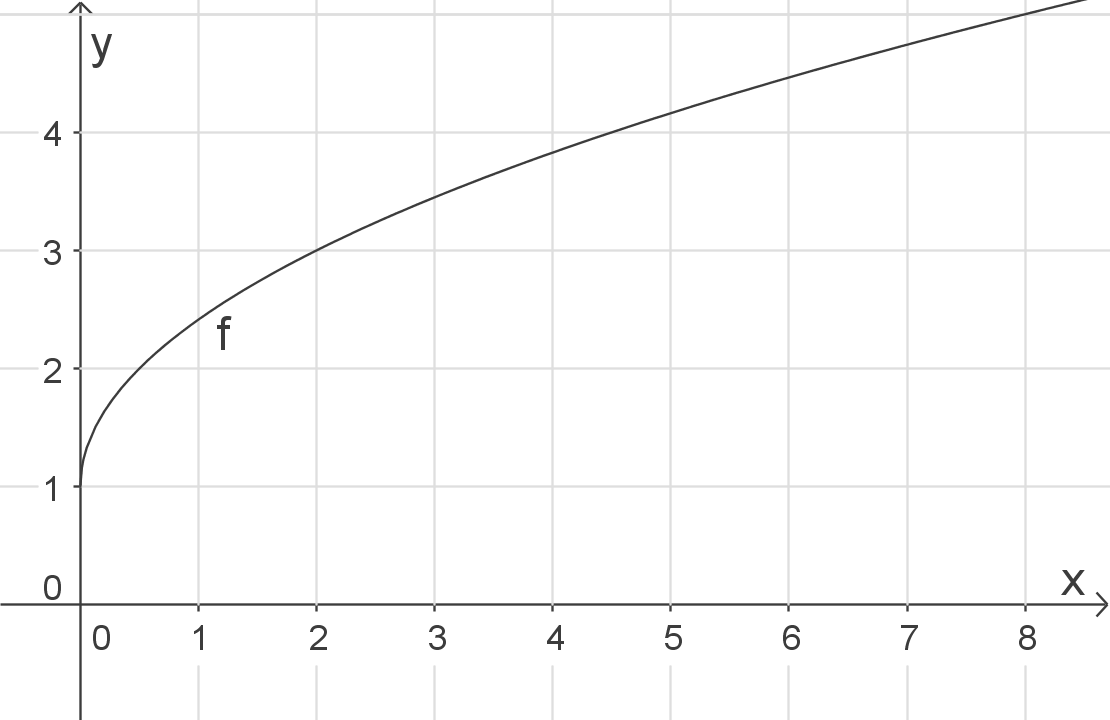 Schaubild herleiten
Das Schaubild von
Schaubild herleiten
Das Schaubild von  geht aus dem Schaubild der Wurzelfunktion hervor durch Stauchung um Faktor 2 in
geht aus dem Schaubild der Wurzelfunktion hervor durch Stauchung um Faktor 2 in  -Richtung und Verschiebung um 1 LE in positive
-Richtung und Verschiebung um 1 LE in positive  -Richtung („nach oben“).
-Richtung („nach oben“).
 Skizze
Skizze
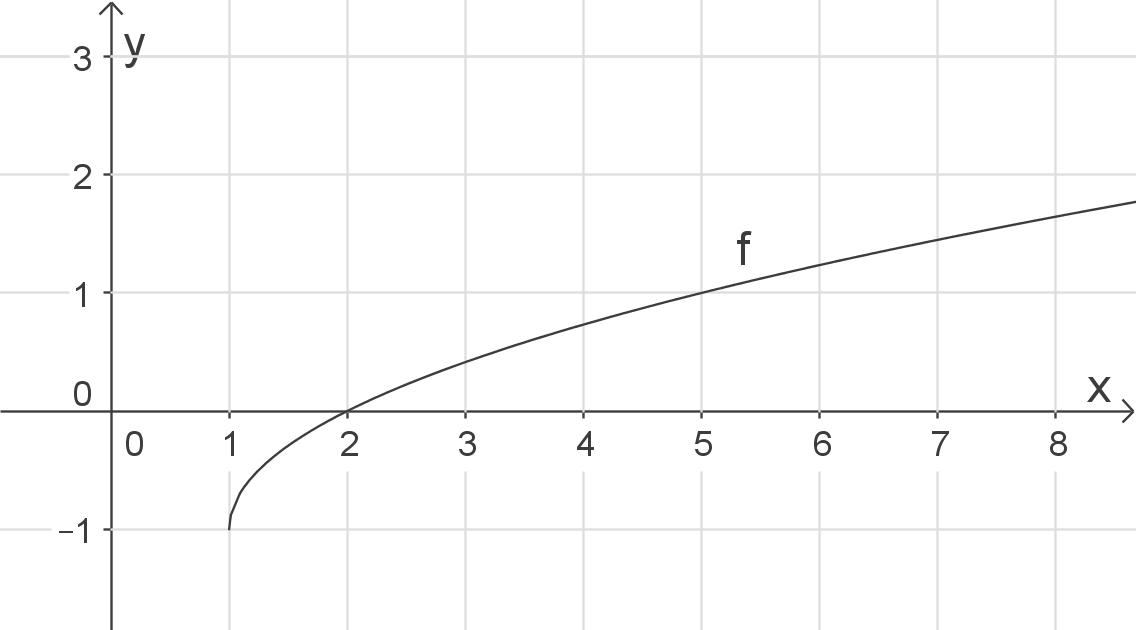 Schaubild herleiten
Das Schaubild von
Schaubild herleiten
Das Schaubild von  geht aus dem Schaubild der Wurzelfunktion hervor durch Verschiebung um 1 LE in positive
geht aus dem Schaubild der Wurzelfunktion hervor durch Verschiebung um 1 LE in positive  -Richtung („nach rechts“) und Verschiebung um 1\,LE in negative
-Richtung („nach rechts“) und Verschiebung um 1\,LE in negative  -Richtung („nach unten“).
-Richtung („nach unten“).
 Skizze
Skizze
 Schaubild herleiten
Das Schaubild von
Schaubild herleiten
Das Schaubild von  geht aus dem Schaubild dem Schaubild der Wurzelfunktion hervor durch Spiegelung an der
geht aus dem Schaubild dem Schaubild der Wurzelfunktion hervor durch Spiegelung an der  -Achse, Streckung um Faktor 2 in
-Achse, Streckung um Faktor 2 in  -Richtung und Spiegelung an der
-Richtung und Spiegelung an der  -Achse.
-Achse.
 Skizze
Skizze
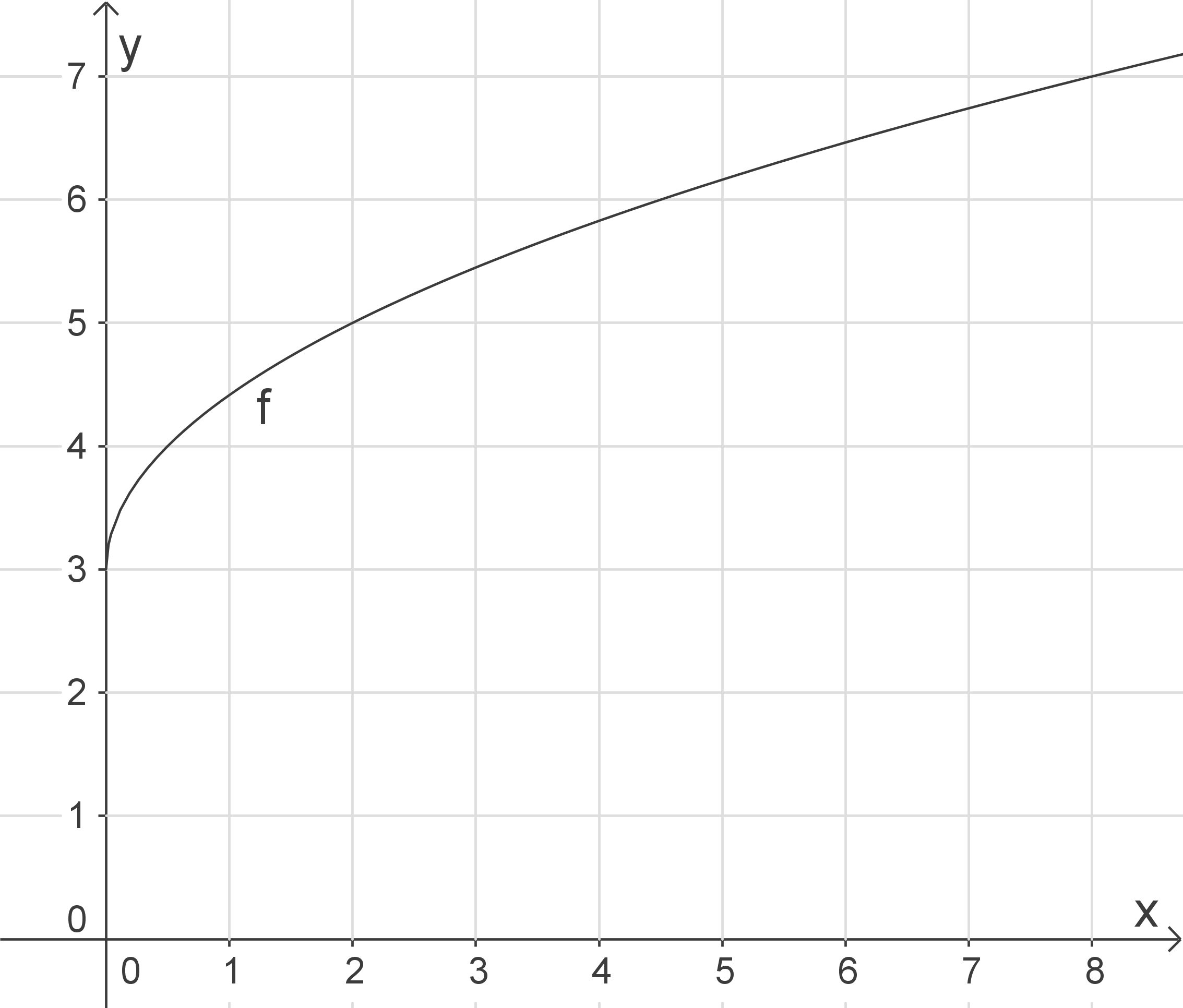 Schaubild herleiten
Das Schaubild von
Schaubild herleiten
Das Schaubild von  geht aus dem Schaubild der Wurzelfunktion hervor durch Stauchung in
geht aus dem Schaubild der Wurzelfunktion hervor durch Stauchung in  -Richtung um Faktor 2 und um Verschiebung in positive
-Richtung um Faktor 2 und um Verschiebung in positive  -Richtung um 3 LE („nach oben“).
-Richtung um 3 LE („nach oben“).
a)

b)

c)

d)

e)

f)

3.
Funktionsgleichung aufstellen
 Verschiebung um 1 LE in positive x-Richtung („nach rechts“) und um 3 LE in positive y-Richtung („nach oben“)
Skizze
Verschiebung um 1 LE in positive x-Richtung („nach rechts“) und um 3 LE in positive y-Richtung („nach oben“)
Skizze
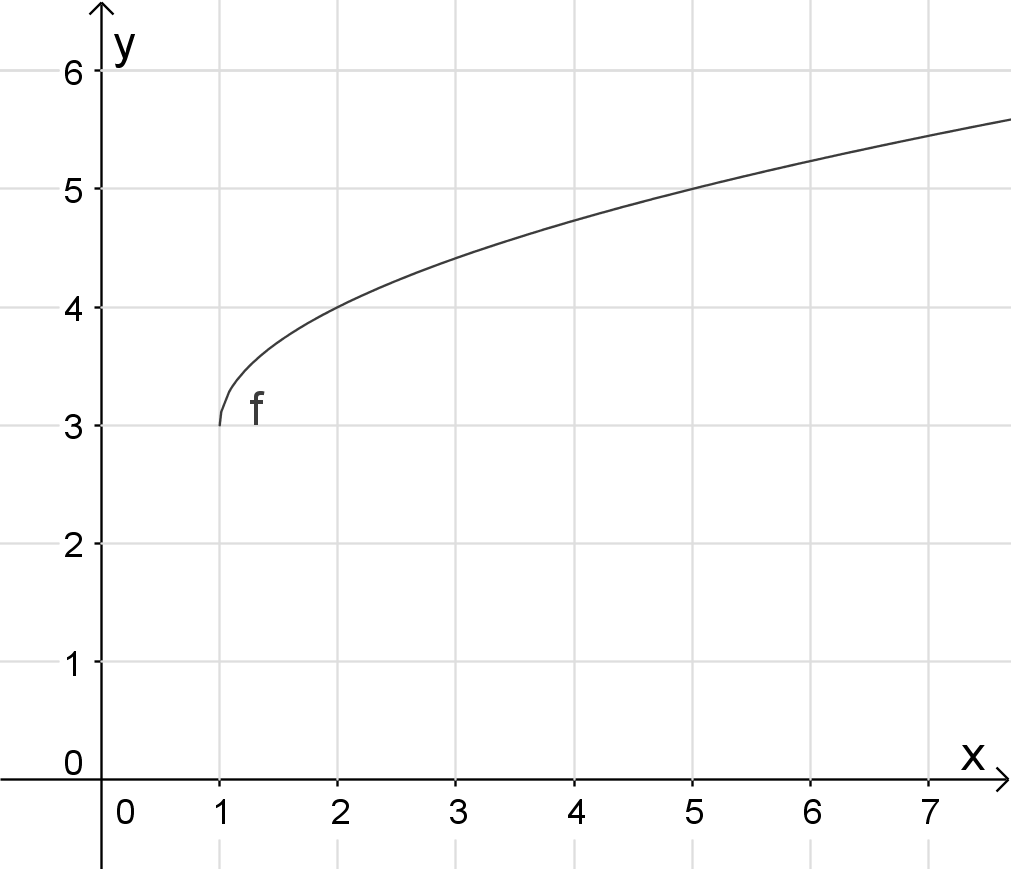 Funktionsterm
Funktionsterm

 Verschiebung um 3 LE in negative x-Richtung („nach links“) und um 4 LE in positive y-Richtung („nach oben“)
Skizze
Verschiebung um 3 LE in negative x-Richtung („nach links“) und um 4 LE in positive y-Richtung („nach oben“)
Skizze
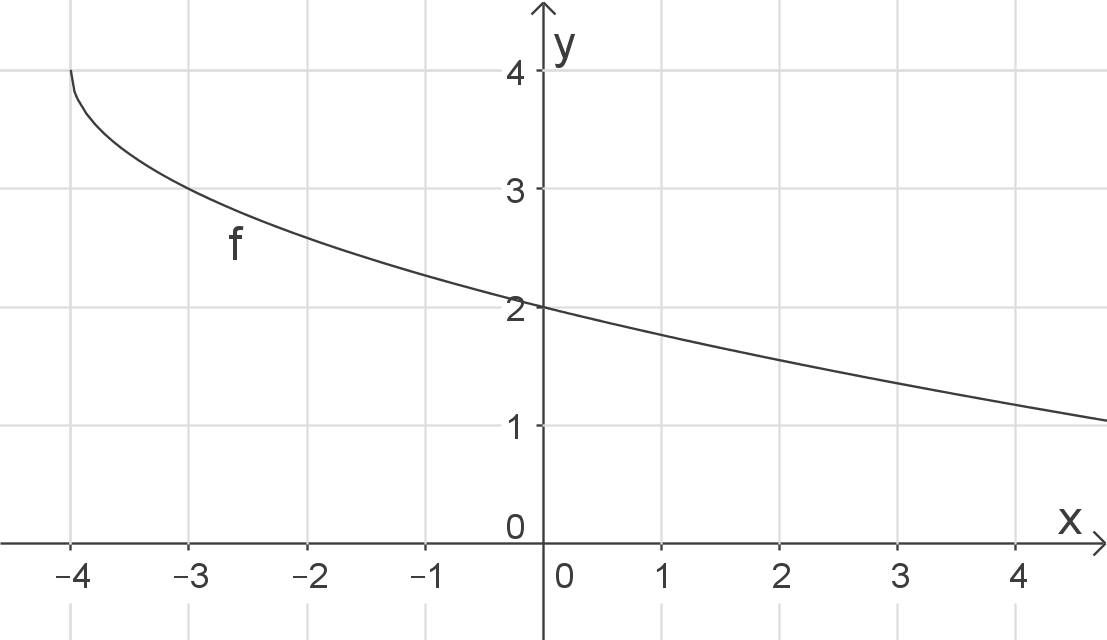 Funktionsterm
Funktionsterm

 Verschiebung um 2 LE in negative x-Richtung („nach links“) und um 4 LE in negative y-Richtung („nach unten“)
Skizze
Verschiebung um 2 LE in negative x-Richtung („nach links“) und um 4 LE in negative y-Richtung („nach unten“)
Skizze
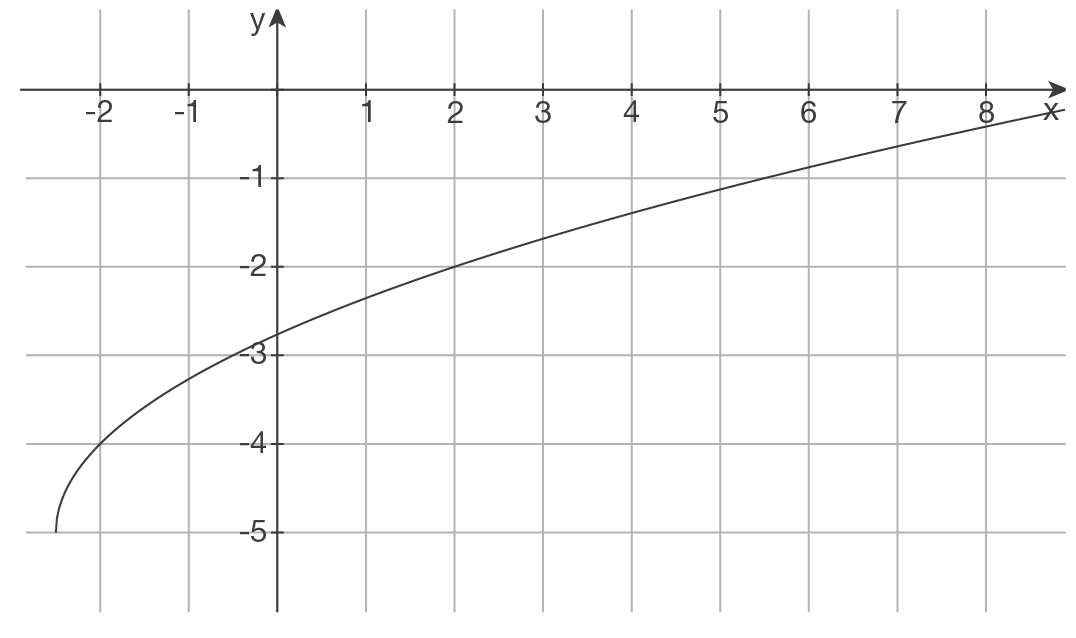 Funktionsterm
Umschreiben des Funktionsterms:
Der neue Funktionsterm lautet also:
Funktionsterm
Umschreiben des Funktionsterms:
Der neue Funktionsterm lautet also:
 Verschiebung um 2 LE in positive y-Richtung („nach oben“) und anschließende Spiegelung an der x-Achse
Skizze
Verschiebung um 2 LE in positive y-Richtung („nach oben“) und anschließende Spiegelung an der x-Achse
Skizze
 Funktionsterm
Funktionsterm

 Verschiebung um 3 LE in positive x-Richtung („nach rechts“) und anschließende Spiegelung an der y-Achse
Skizze
Verschiebung um 3 LE in positive x-Richtung („nach rechts“) und anschließende Spiegelung an der y-Achse
Skizze
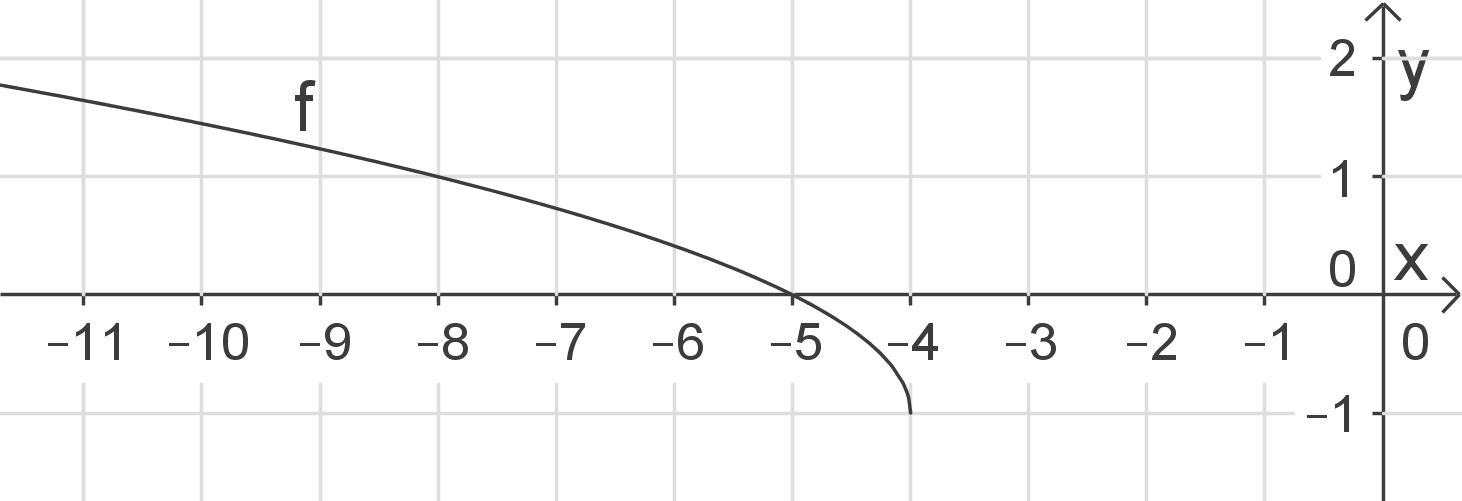 Funktionsterm
Funktionsterm

 Verschiebung um 1 LE in positive y-Richtung („nach oben“) und um 3 LE in negative x-Richtung („nach links“)
Skizze
Verschiebung um 1 LE in positive y-Richtung („nach oben“) und um 3 LE in negative x-Richtung („nach links“)
Skizze
 Funktionsterm
Funktionsterm

a)

b)

c)

d)

e)

f)
