Pfadmultiplikationsregel und Pfadadditionsregel
Ein Baumdiagramm kann helfen, dir einen Überblick über mehrstufige, aber auch einstufige Zufallsexperimente zu verschaffen. Dabei stellen einzelne Äste entweder Ergebnisse oder manchmal auch Ereignisse eines Zufallsexperiments dar. Die Äste sind dann mit den zugehörigen Wahrscheinlichkeiten beschriftet.
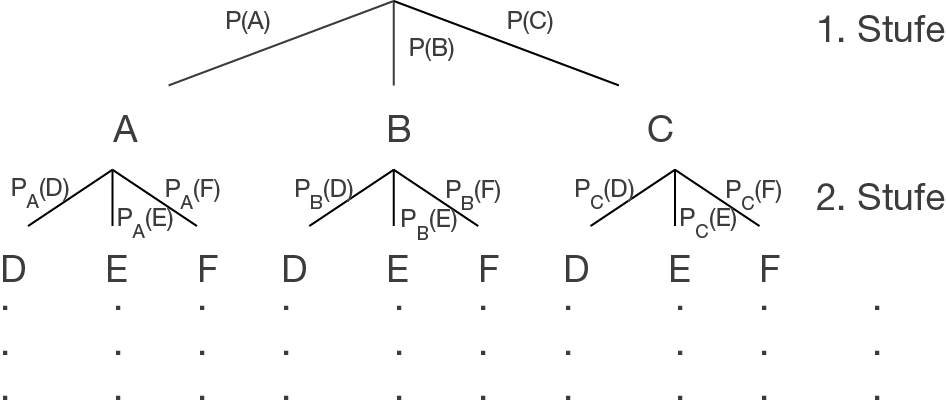
ist die bedingte Wahrscheinlichkeit dafür, dass Ereignis 
eintritt, wenn in der vorherigen Stufe des Zufallsexperiments Ereignis 
eingetreten ist. Ein Weg von der Wurzel des Baumes zu einem der Endergebnisse wird Pfad genannt.
Die 2. Pfadregel oder Pfadadditionsregel besagt, dass die Wahrscheinlichkeiten mehrerer Pfade addiert werden können:
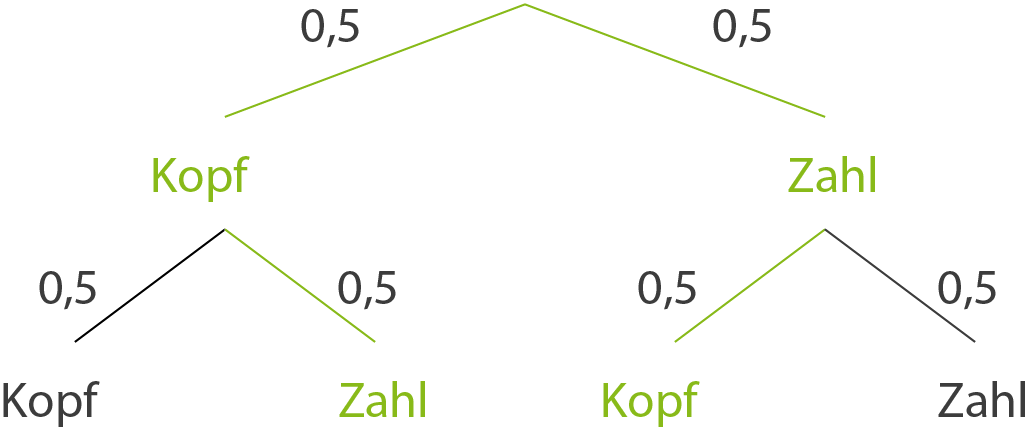
Die Wahrscheinlichkeit dafür, dass einmal „Zahl“ und einmal „Kopf“ erscheint ergibt sich aus der Wahrscheinlichkeit zweier Pfade. Diese sind im folgenden Diagramm grün markiert.
Pfadregeln
Die 1. Pfadregel oder Pfadmultiplikationsregel besagt, dass sich die Wahrscheinlichkeiten entlang eines Pfades multiplizieren und man so die Gesamtwahrscheinlichkeit des Pfades erhält:Beispiel
Wir betrachten das zweimalige Werfen einer Münze:Die Wahrscheinlichkeit dafür, dass einmal „Zahl“ und einmal „Kopf“ erscheint ergibt sich aus der Wahrscheinlichkeit zweier Pfade. Diese sind im folgenden Diagramm grün markiert.
Mit beiden Pfadregeln folgt:
Vollständige Gleichung anzeigen
1.
Ein idealer Würfel wird dreimal geworfen.
a)
Wie groß ist die Wahrscheinlichkeit dreimal hintereinander eine 6 zu werfen?
b)
Wie groß ist die Wahrscheinlichkeit, dass die Augensumme größer als 16 ist?
c)
Könnte man das Zufallsexperiment auch durch eine Urnenziehung mit bzw. ohne Zurücklegen darstellen?
2.
Aus einer Urne mit vier Kugeln (rot, gelb, blau, schwarz) wird zweimal ohne Zurücklegen gezogen. Gib die Ergebnismengen an und zeichne ein passendes Baumdiagramm. Wie groß ist die Wahrscheinlichkeit, dass zuerst rot und dann gelb gezogen wird?
3.
In einem McDonald‘s Restaurant steht ein Glücksrad mit sechs Gewinnfeldern. Alle Gewinnfelder sind gleich groß. Dreht man das Rad, so zeigt ein Zeiger genau auf einen Gutschein (Big Mac, kleines Getränk, Happy Meal, Cheeseburger, kleine Pommes, Kaffee). Peter darf zweimal drehen.
a)
Wie groß ist die Wahrscheinlichkeit, dass er mit zwei Cheeseburgern nach Hause geht?
b)
Wie groß ist die Wahrscheinlichkeit, dass er ohne einen Big Mac nach Hause geht?
4.
Aus einer Urne mit vier roten und vier schwarzen Kugeln werden zwei Kugeln mit Zurücklegen gezogen. Führe den Zufallsversuch auf zwei verschiedene Arten durch und gib die Ergebnismenge an:
a)
Bei der Ziehung wird die Reihenfolge berücksichtigt.
b)
Bei der Ziehung wird die Reihenfolge nicht berücksichtigt.
c)
Wie ändert sich die Wahrscheinlichkeit jeweils?
5.
Eine Münze wird zweimal geworfen. Martin fragt sich nun, ob zwei gleiche oder zwei verschiedene Ereignisse wahrscheinlicher sind. Was meinst du?
6.
Bei einer Polizeikontrolle werden 
der Autos kontrolliert. Vier befreundete Urlauber fahren mit ihren Autos hintereinander in die Polizeikontrolle. Wie groß ist die Wahrscheinlichkeit, dass
a)
alle vier kontrolliert werden?
b)
nur die ersten beiden Autos kontrolliert werden?
c)
keiner der vier kontrolliert wird?
d)
genau drei kontrolliert werden?
7.
Nach Einwurf eines Euros erhält man von einem Glücksspielautomaten ein Los, auf das eine siebenstellige Zahl gedruckt ist, die nur aus den Ziffern 1 und 2 besteht (z.B. 
). Der Automat erzeugt die Ziffer 1 mit der Wahrscheinlichkeit 0,6 und die Ziffer 2 mit der Wahrscheinlichkeit 0,4. Bestimme die Wahrscheinlichkeit für folgende Ereignisse:
- A: „Die aufgedruckte Zahl endet mit
.“
- B: „Die aufgedruckte Zahl ist größer als
.“
8.
Bei einem Handballspiel beträgt die Wahrscheinlichkeit, dass der Torhüter aufgrund von Verletzungen ausfällt, 
. Für die 6 Feldspieler beträgt die Wahrscheinlichkeit 
. Mit welcher Wahrscheinlichkeit wird während des Spiels keiner der 7 Spieler verletzt?
9.
Wie oft muss man würfeln, um mit 
Wahrscheinlichkeit mindestens eine Eins zu erhalten?
10.
Es findet ein Elfmeterschießen zwischen Mannschaft und 
statt. Jeder Spieler der Mannschaft verwandelt einen Elfmeter mit einer Wahrscheinlichkeit von 
. Bei Mannschaft sind es nur 
.
a)
Wie viel Elfmeter muss Mannschaft mindestens schießen, um mit einer Wahrscheinlichkeit von 
mindestens einen Treffer zu erzielen?
b)
Als die Mannschaften ins Elfmeterschießen kamen, stand es bereits 
. Im Elfmeterschießen hat jede Mannschaft bereits dreimal geschossen. Wie groß ist die Wahrscheinlichkeit, dass der aktuelle Spielstand unentschieden ist?
11.
Statistiken haben gezeigt, dass 
der männlichen Jugendlichen und 
der weiblichen Jugendlichen im Alter von 13 Jahren anfangen zu rauchen.
a)
Wie groß ist die Wahrscheinlichkeit, aus einer Stichprobe von 12 Jugendlichen mit 5 Mädchen und 7 Jungen, 5 Nicht-Raucherinnen zu finden?
b)
Wie viele männliche Jugendliche müsste man aus der Stichprobe befragen, um mit einer Wahrscheinlichkeit von mehr als 
mindestens einen Raucher zu finden?
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
Wahrscheinlichkeiten bestimmen
Die Ergebnismenge ist
a)
Die Wahrscheinlichkeit, dreimal hintereinander eine Sechs zu werfen, ist:
b)
Soll die Augensumme größer als 16 sein, so gibt es dafür mehrere Würfelkombinationen:
c)
Es handelt sich um ein dreistufiges Zufallsexperiment, das durch ein Urnenexperiment mit Zurücklegen ersetzt werden könnte. Z.B. könnten sechs Kugeln in der Urne liegen mit der Beschriftung 1 bis 6.
2.
Ergebnismenge angeben und Baumdiagramm zeichnen
(rot 
r, gelb g, blau b, schwarz s)
Ein mögliches Baumdiagramm ist:
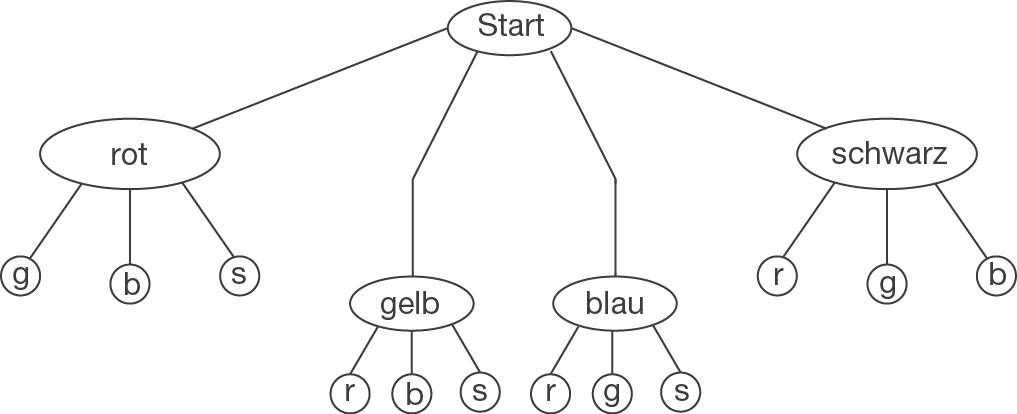Für die Wahrscheinlichkeit, zuerst rot und dann gelb zu ziehen, gilt nach der Pfadregel:
3.
Wahrscheinlichkeiten bestimmen
(Big Mac=B, kleines Getränk=G, Happy Meal=H, Cheeseburger=C, kleine Pommes=P, Kaffee=K)
Es ergibt sich die Ergebnismenge:
a)
b)
Bei einmaligem Drehen wird mit einer Wahrscheinlichkeit von 
kein Big Mac getroffen. Die Wahrscheinlichkeit dafür, dass bei zweimaligem Drehen kein Big Mac getroffen wird, ist dann:
4.
Ergebnismenge angeben
(rot=r, schwarz=s)
a)
Die Ergebnismenge ist:
b)
Die Ergebnismenge ist:
c)
Es wird mit Zurücklegen gezogen. Deshalb beträgt die Wahrscheinlichkeit für jede beliebige Kombination 
.
In a) beträgt die Wahrscheinlichkeit jeweils 
für eines der Ereignisse.
In b) sieht diese Wahrscheinlichkeit anders aus: Für die Kombinationen 
und 
gibt es jeweils eine Möglichkeit. Deshalb beträgt die Wahrscheinlichkeit für und für jeweils .
Für die Kombination 
gibt es aber zwei Möglichkeiten, nämlich und 
. Deshalb beträgt die Wahrscheinlichkeit für diese Kombination 
.
5.
Wahrscheinlichkeiten vergleichen
Das Baumdiagramm sieht folgendermaßen aus:
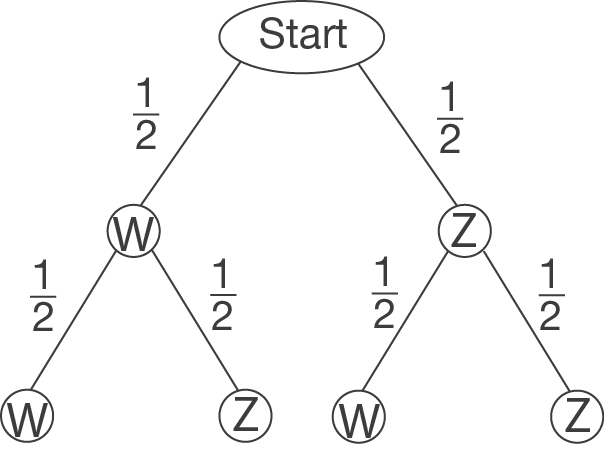Es gilt:
Damit sind die beiden Ereignisse gleich wahrscheinlich.
6.
Wahrscheinlichkeiten bestimmen
Stellt man sich die Pfade in einem reduzierten Baumdiagramm vor so ergibt sich mit 
für Kontrolle:
a)
b)
c)
d)
7.
Wahrscheinlichkeiten bestimmen
Das Drucken eines Loses könnte man in einem Baumdiagramm darstellen, allerdings würde dieses zu umfangreich werden. Deshalb beschränkt man sich auf die für die Aufgabe relevanten Pfade. Bei wären das die Pfade, die die Zahlen mit Endung 
haben also z.B. (
).
Es handelt sich um ein dreistufiges Zufallsexperiment, bei dem das Ergebnis „1“ mit der Wahrscheinlichkeit 
genau dreimal auftreten soll. Die ersten 4 Ziffern spielen keinerlei Rolle, denn sie sind für unser Ereignis nicht relevant.
Die aufgedruckten Zahlen die größer als 
sind, sind jene, die als erste 4 Ziffern eine 2 haben. Es handelt sich also um ein vierstufiges Zufallsexperiment, bei dem das Ergebnis 2 mit der Wahrscheinlichkeit 
genau viermal auftreten soll. Die letzten drei Ziffern spielen dabei keine Rolle.
8.
Wahrscheinlichkeiten bestimmen
Stellst du dir das Geschehen als Baumdiagramm vor und betrachtest die Wahrscheinlichkeiten dafür, dass die Spieler nicht ausfallen, so ergibt sich für den Torhüter 0,99 und für die 6 anderen Spieler 
.
Zusammen also für das Ereignis : „Kein Spieler fällt aufgrund einer Verletzung aus“:
Mit einer Wahrscheinlichkeit von 
wird also kein Spieler während des gesamten Spiels verletzt.
9.
Anzahl der Würfe bestimmen
Es gilt:
.
Es ergibt sich daher folgende Gleichung für die Anzahl 
der nötigen Würfe:
![\(\begin{array}[t]{rll}
0,99=&1-\left(\dfrac{5}{6}\right)^n\\[5pt]
\left(\dfrac{5}{6}\right)^n=&0,01\\[5pt]
n=& \dfrac{\log \left(0,01\right)}{\log \left(\frac{5}{6}\right)}\approx 25,26
\end{array}\)](https://mathjax.schullv.de/6ed3b6bd6475eb78430b0e1bbaea84a7e1ee3a8b5a07a1066ee353ed08a94131?color=5a5a5a)
Man muss also 26 mal werfen, um mit einer Wahrscheinlichkeit von mehr als 
mindestens eine Eins zu würfeln.
10.
Wahrscheinlichkeiten bestimmen
a)
Soll mit einer Wahrscheinlichkeit von mindestens ein Treffer erzielt werden, dann muss gelten:
Mannschaft muss also mindestens 3 Elfmeter schießen, um mit einer Wahrscheinlichkeit von mindestens einen Treffer zu erzielen.
b)
Da der Spielstand vor dem Elfmeterschießen schon war, gibt es nach dreimaligem Schießen folgende mögliche Ergebnisse für Unentschieden: , 
; 
, 
.
Stellst du dir die Situation als Baumdiagramm vor, so ergeben sich die möglichen Pfade. Über die 1. und 2. Pfadregel kannst du die Wahrscheinlichkeiten bestimmen.
Dafür gilt für die einzelnen Trefferwahrscheinlichkeiten der Mannschaften und :
Addierst du diese Wahrscheinlichkeiten, so erhältst du:
Also beträgt die Wahrscheinlichkeit für ein Unentschieden nach dreimaligem Schießen ca. 
.
Ereignis : 
Ereignis : 
Ereignis : 
Ereignis : 
11.
Wahrscheinlichkeiten bestimmen
Statistiken haben gezeigt, dass der männlichen Jugendlichen und der weiblichen Jugendlichen im Alter von 13 Jahren anfangen zu rauchen.
a)
Die Wahrscheinlichkeit, dass ein Mädchen raucht beträgt . Die Wahrscheinlichkeit, dass ein Mädchen nicht raucht, beträgt 
. Die Wahrscheinlichkeit, dass alle fünf Mädchen in der Stichprobe nicht rauchen, beträgt
b)
Die Wahrscheinlichkeit, dass Jungen nicht rauchen, beträgt 
. Es ergibt sich folgende Rechnung:
Es müssen mindestens 3 männliche Jugendliche befragt werden, um mit einer Wahrscheinlichkeit von mehr als 
mindestens einen Raucher zu finden.