Geraden im Raum

Eine Gerade im dreidimensionalen Raum hat 3 Komponenten für je eine Richtung im Raum (z.B.: $x_1,\;x_2$ und $x_3$ -Richtung). Ist eine Komponente des Stütz- und/oder Richtungsvektors einer Geraden ungleich Null, so durchläuft diese Gerade diese Richtung im Raum. Eine solche Gerade kann auf eine Ebene projiziert werden, wie im Schaubild dargestellt wurde.

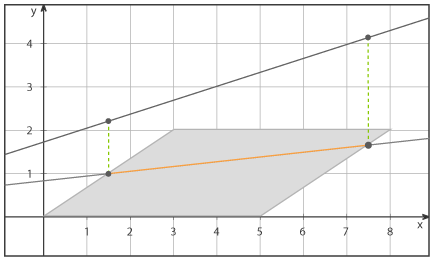Wird eine Projektionsebene angegeben, so erhältst du die projizierte Gerade, indem du die Komponenten des Stütz- und Richtungsvektors gleich Null setzt, die nicht von der Projektionsebene erfasst werden.

Beispiel

Projiziere die Gerade
$g:\;\overrightarrow{x}=\begin{pmatrix}1\\2\\3\end{pmatrix} + t \cdot \begin{pmatrix}4\\4\\4\end{pmatrix}$
auf die $x_1x_3$ -Ebene.
In der $x_1x_3$ -Ebene sind alle $x_2$ -Koordinaten gleich Null, setze also in der Geradengleichung zu $g$ die $x_2$ -Komponenten gleich Null:
$g_{x_1x_3}:\;\overrightarrow{x}=\begin{pmatrix}1\\0\\3\end{pmatrix} + t \cdot \begin{pmatrix}4\\0\\4\end{pmatrix}$