Erwartungswert
Der Erwartungswert einer Zufallsvariable  zu einem Zufallsexperiment mit dem Ergebnisraum
zu einem Zufallsexperiment mit dem Ergebnisraum  gibt den Wert an, den die Zufallsvariable im Mittel annimmt. Im Schnitt wäre bei der wiederholten Durchführung des Experimentes also in etwa ein Ergebnis in der Nähe des Erwartungswerts zu erwarten. Er berechnet sich wie folgt:
gibt den Wert an, den die Zufallsvariable im Mittel annimmt. Im Schnitt wäre bei der wiederholten Durchführung des Experimentes also in etwa ein Ergebnis in der Nähe des Erwartungswerts zu erwarten. Er berechnet sich wie folgt:
 =
= =
= +
+ +
+ +
+ Sollst du den Erwartungswert berechnen, überlege dir also zunächst welche möglichen Ausgänge das Zufallsexperiment haben kann und welche Wahrscheinlichkeiten diese haben.
Sollst du den Erwartungswert berechnen, überlege dir also zunächst welche möglichen Ausgänge das Zufallsexperiment haben kann und welche Wahrscheinlichkeiten diese haben.
 Hierbei gilt also
Hierbei gilt also  Im Schnitt ist beim Werfen eines Würfels also ein Ergebnis um
Im Schnitt ist beim Werfen eines Würfels also ein Ergebnis um  zu erwarten.
zu erwarten.
Beispiel
Betrachte das Werfen eines gleichmäßigen sechsseitigen Würfels. Hierbei hat jede Zahl die gleiche Wahrscheinlichkeit:
1.
Aus einer Urne mit 2 schwarzen und 10 grünen Kugeln werden nacheinander, ohne Zurücklegen, so lange einzelne Kugeln entnommen, bis die erste grüne Kugel kommt.
Wie oft muss man durchschnittlich ziehen?
Wie oft muss man durchschnittlich ziehen?
2.
Ein mysteriöser Mann bietet an einer Straßenecke folgendes Würfelspiel an:
Geworfen werden zwei Würfel und dann wird die Augensumme betrachtet. Beträgt diese 12, werden 5 Euro ausgezahlt, beträgt diese 10 oder 11, werden 2 Euro ausgezahlt. In allen anderen Fällen erfolgt keine Auszahlung.
Wie viel Geld wird durchschnittlich ausgezahlt?
Geworfen werden zwei Würfel und dann wird die Augensumme betrachtet. Beträgt diese 12, werden 5 Euro ausgezahlt, beträgt diese 10 oder 11, werden 2 Euro ausgezahlt. In allen anderen Fällen erfolgt keine Auszahlung.
Wie viel Geld wird durchschnittlich ausgezahlt?
3.
In einer Lostrommel sind 20 Lose. Davon enthalten 12 Lose 1 Gewinnpunkt, die anderen 8 Lose 0 Gewinnpunkte. Mit den gesammelten Gewinnpunkten kann man sich dann einen Preis aussuchen. Es werden drei Lose auf einmal gezogen. Wie viele Punkte erhält man im Durchschnitt?
4.
Berechnen Sie den Erwartungswert für eine  -verteilte Zufallsvariable mit der Definition des Erwartungswerts, ohne Verwendung der Formel
-verteilte Zufallsvariable mit der Definition des Erwartungswerts, ohne Verwendung der Formel  .
.
5.
In einem Sparschwein befinden sich zehn 20 Cent-Münzen, sieben 50 Cent-Münzen, und drei 2 Euro-Münzen. Sarah plündert ihr Sparschwein und
a)
entnimmt eine Münze. Mit wie viel Geld kann Sarah im Durchschnitt rechnen?
b)
entnimmt zwei Münzen. Mit wie viel Geld kann Sarah jetzt durchschnittlich rechnen?
6.
Eine Laplace Münze wird so oft geworfen, bis zweimal hintereinander die gleiche Seite oben liegen bleibt. Insgesamt wird aber höchstens  -mal geworfen. Die Zufallsgröße
-mal geworfen. Die Zufallsgröße  sei die Anzahl der Würfe,
sei die Anzahl der Würfe,  sei der Erwartungswert.
sei der Erwartungswert.
a)
Bestimme  ,
,  und
und  .
.
b)
Wie groß ist die Wahrscheinlichkeit, bei  -maligen Würfen immer abwechselnd beide Seiten zu erhalten?
-maligen Würfen immer abwechselnd beide Seiten zu erhalten?
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
Berechnung der durchschnittlichen Züge
Wird als Erstes eine grüne Kugel gezogen, wird das Zufallsexperiment abgebrochen. Die Wahrscheinlichkeit hierfür ist  .
Wird als Erstes eine schwarze und dann eine grüne Kugel gezogen, wird das Zufallsexperiment abgebrochen. Die Wahrscheinlichkeit hierfür ist
.
Wird als Erstes eine schwarze und dann eine grüne Kugel gezogen, wird das Zufallsexperiment abgebrochen. Die Wahrscheinlichkeit hierfür ist  .
Sind die ersten beiden Kugeln schwarz und die dritte grün, wird das Zufallsexperiment wieder abgebrochen. Die Wahrscheinlichkeit hierfür ist
.
Sind die ersten beiden Kugeln schwarz und die dritte grün, wird das Zufallsexperiment wieder abgebrochen. Die Wahrscheinlichkeit hierfür ist  Die Situation kannst du in folgender Tabelle veranschaulichen:
Die Situation kannst du in folgender Tabelle veranschaulichen:
Für den Erwartungswert  ergibt sich mit der Formel:
Man braucht also durchschnittlich ungefähr 1,18 Züge.
ergibt sich mit der Formel:
Man braucht also durchschnittlich ungefähr 1,18 Züge.
| Ergebnis | Anzahl der Züge |
| g | 1 |
| sg | 2 |
| ssg | 3 |
2.
Berechnung der durchschnittlichen Auszahlung
Die Situation kannst du in folgender Tabelle veranschaulichen:
Für den Erwartungswert  ergibt sich mit der Formel:
Man bekommt also durchschnittlich ungefähr 42 Cent ausgezahlt.
ergibt sich mit der Formel:
Man bekommt also durchschnittlich ungefähr 42 Cent ausgezahlt.
| Augensumme | Auszahlung |
| 12 | 5 |
| 11 | 2 |
| 10 | 2 |
| 2 bis 9 | 0 |
3.
Berechnung der durchschnittlichen Gewinnpunktanzahl
Es werden drei Lose auf einmal gezogen. Du kannst diese Situation in einem Baumdiagramm darstellen. Das „Auf-einmal-Ziehen“ entspricht dem „Ziehen ohne Zurücklegen“.
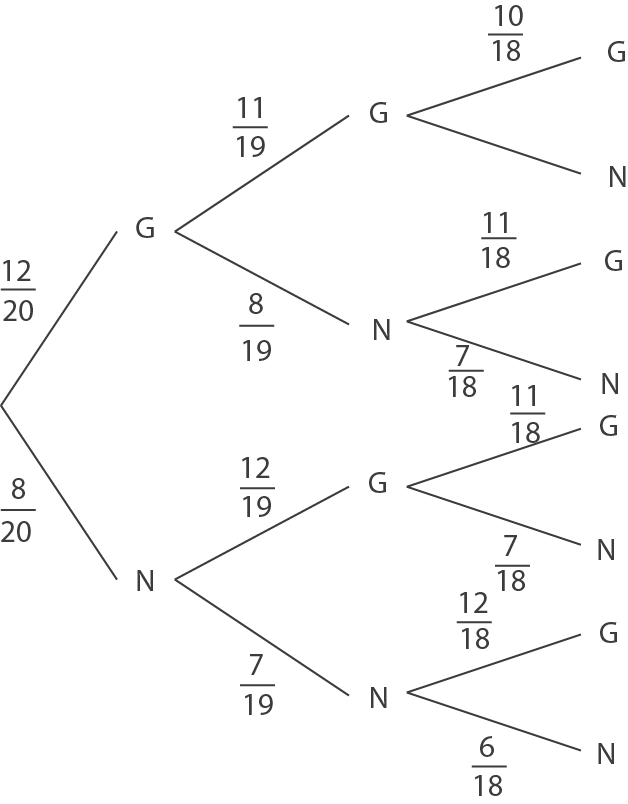 Es gibt vier mögliche Ausgänge bei diesem Zufallsexperiment: 0 Punkte, 1 Punkt, 2 Punkte oder 3 Punkte. Aus dem Baumdiagramm folgen die Wahrscheinlichkeiten:
Es gibt vier mögliche Ausgänge bei diesem Zufallsexperiment: 0 Punkte, 1 Punkt, 2 Punkte oder 3 Punkte. Aus dem Baumdiagramm folgen die Wahrscheinlichkeiten:
Für den Erwartungswert  ergibt sich mit der Formel:
Man bekommt also durchschnittlich 1,8 Gewinnpunkte.
ergibt sich mit der Formel:
Man bekommt also durchschnittlich 1,8 Gewinnpunkte.

| Ergebnis | Anzahl Punkte |
| drei Punkte | 3 |
| zwei Punkte | 2 |
| ein Punkt | 1 |
| kein Punkt | 0 |
4.
Berechnung des Erwartungswertes
Berechne den Erwartungswert für eine  -verteilte Zufallsvariable mit der Definition des Erwartungswerts ohne Verwendung der Formel
-verteilte Zufallsvariable mit der Definition des Erwartungswerts ohne Verwendung der Formel  .
Damit ergibt sich für den Erwartungswert:
.
Damit ergibt sich für den Erwartungswert:
 =
= =
= =
=
5.
Berechnung der durchschnittlichen Geldmenge
a)
Die Wahrscheinlichkeit, eine 20 Cent-Münze zu ziehen, beträgt:  Die Wahrscheinlichkeit, eine 50 Cent-Münze zu ziehen, beträgt:
Die Wahrscheinlichkeit, eine 50 Cent-Münze zu ziehen, beträgt:  Die Wahrscheinlichkeit, eine 2 Euro-Münze zu ziehen, beträgt:
Die Wahrscheinlichkeit, eine 2 Euro-Münze zu ziehen, beträgt:  Durchschnittlich sind daher
Euro zu erwarten - im Durchschnitt also 57,5 Cent.
Durchschnittlich sind daher
Euro zu erwarten - im Durchschnitt also 57,5 Cent.
b)
Es ergeben sich beim zweimaligen Ziehen folgende Wahrscheinlichkeiten:
0,4 Euro:

 0,7 Euro:
0,7 Euro:

 2,2 Euro:
2,2 Euro:

 1,0 Euro:
1,0 Euro:

 2,5 Euro:
2,5 Euro:

 4,0 Euro:
4,0 Euro:

 Es ist
Im Durchschnitt kann Sarah mit 1,15 Euro rechnen.
Es ist
Im Durchschnitt kann Sarah mit 1,15 Euro rechnen.
6.
Berechnung von Erwartungswert und Wahrscheinlichkeit
a)
Die Zufallsgröße  gibt die Anzahl der Würfe an,
gibt die Anzahl der Würfe an,  ihren Erwartungswert.
Fall
ihren Erwartungswert.
Fall  :
Für
:
Für  erhältst du nun folgende Möglichkeiten:
Fall
erhältst du nun folgende Möglichkeiten:
Fall  :
Für
:
Für  erhältst du nun folgende Möglichkeiten:
Für
erhältst du nun folgende Möglichkeiten:
Für  erhältst du nun folgende Möglichkeiten:
Fall
erhältst du nun folgende Möglichkeiten:
Fall  :
Für
:
Für  erhältst du nun folgende Möglichkeiten:
Für
erhältst du nun folgende Möglichkeiten:
Für  erhältst du nun folgende Möglichkeiten:
Für
erhältst du nun folgende Möglichkeiten:
Für  erhältst du nun folgende Möglichkeiten:
erhältst du nun folgende Möglichkeiten:
b)
Der erste Wurf kann entweder Kopf oder Zahl sein, ist also beliebig. Die restlichen  Würfe sind festgelegt (je nachdem, ob zuerst Kopf oder zuerst Zahl gewürfelt wurde).
Die Wahrscheinlichkeit für jeden einzelnen Wurf ist nach wie vor
Würfe sind festgelegt (je nachdem, ob zuerst Kopf oder zuerst Zahl gewürfelt wurde).
Die Wahrscheinlichkeit für jeden einzelnen Wurf ist nach wie vor 
 . Die Wahrscheinlichkeit, dass abwechselnd Kopf und Zahl gewürfelt werden, sei
. Die Wahrscheinlichkeit, dass abwechselnd Kopf und Zahl gewürfelt werden, sei  . Dann gilt:
. Dann gilt:
