Nullstellen und Schnittpunkte mit der y-Achse

Schnittpunkte mit der $\boldsymbol{x}$ -Achse

Die Schnittpunkte des Graphen einer Funktion $f$ mit der $x$ -Achse haben folgende Form :

$S_x(x \mid 0)$

$S^x_i(x_i\mid 0)$

Dabei sind die $x_i$ die Nullstellen von $f$ . Du kannst sie also berechnen, indem du die Gleichung $f(x) = 0$ löst.

Beispiel

$f(x) = x^2-4$

Setze $f(x) = 0$ und löse nach $x$ auf:

$\begin{array}{llllllll} x^2-4&=&0& \mid +4\\ x^2&=&4& \mid \sqrt{\;} \\ x_0&=&-2 \\ x_1&=&2 \\ \end{array}$

Die Schnittpunkte des Graphen von $f$ mit der $x$ -Achse ergeben sich also zu $S_{x_0}(-2\mid 0)$ und $S_{x_1}(2\mid 0)$ .

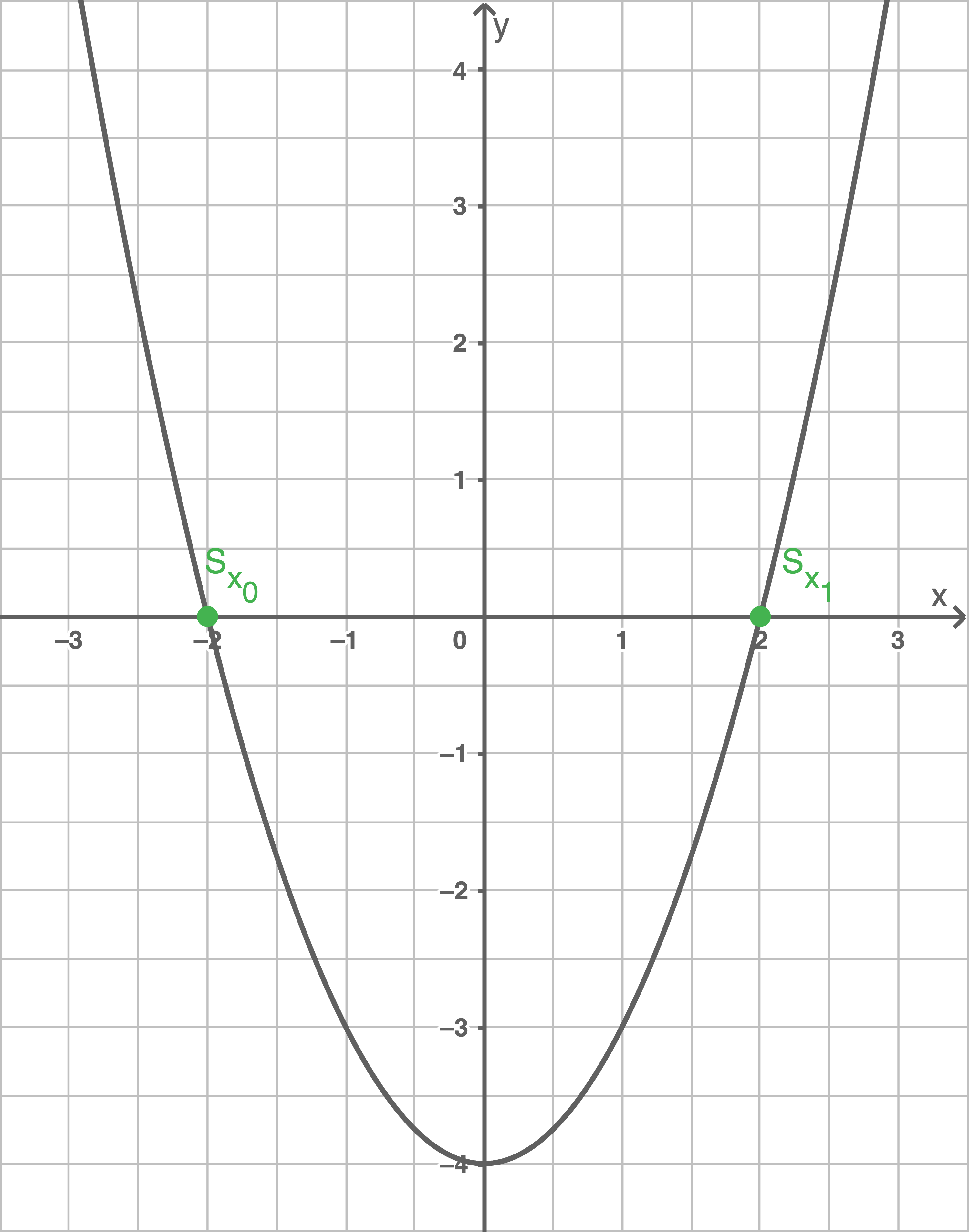
Nullstellen eingezeichnet in die Beispielfunktion x^2-4

Nullstellen der Parabel

Schnittpunkte mit der $\boldsymbol{y}$ -Achse

Der Graph einer Funktion $f$ kann nur einen Schnittpunkt mit der $y$ -Achse besitzen. Dieser hat folgende Form:

$S_y(0\mid f(0))$

$S^y(0\mid f(0))$

Du berechnest dessen Koordinaten also, indem du $0$ in $f(x)$ einsetzt.

Beispiel

$f(x) = x^2-4$

Berechne $f(0)$ :

$0^2-4=-4$

Der Schnittpunkt des Graphen von $f$ mit der $y$ -Achse ergibt sich also zu $S_y(0\mid -4)$ .

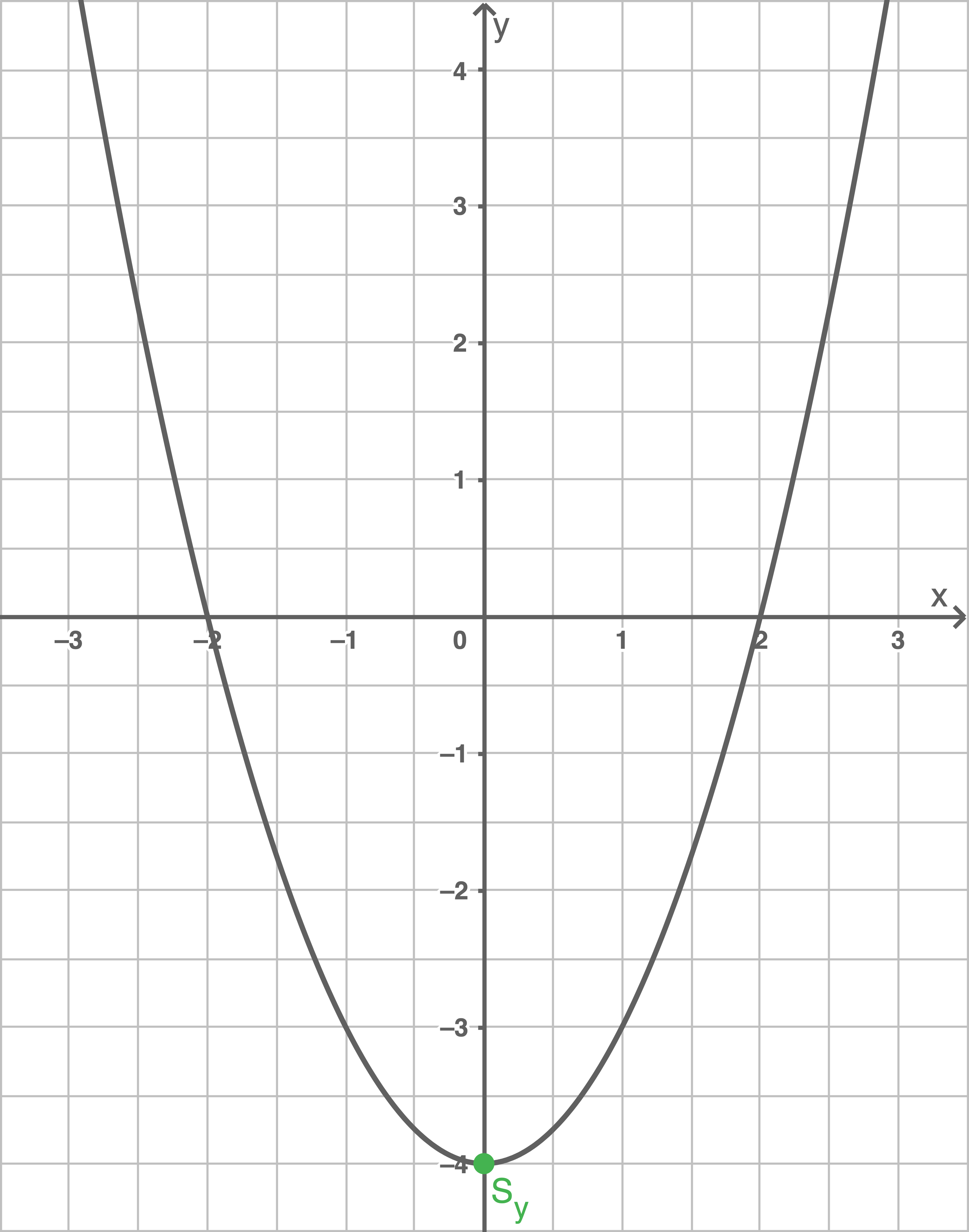
y Achsenabschnitt eingezeichnet in die Beispielfunktion x^2-4

Schnittpunkt der Parabel mit der y-Achse

Berechne die Schnittpunkte von $K_f$ mit den Koordinatenachsen.

$f\left(x\right)=\left(x+2\right)^2$

$f\left(x\right)=-\left(x-1\right)^2+4x-4$

$f\left(x\right)=x\left(x+3\right)^3$

$f\left(x\right)=x^2+1$

Berechne die Schnittpunkte von $K_f$ mit den Koordinatenachsen.

$f\left(x\right)=x^3+x^2-6x$

$f\left(x\right)=x^4-5x^2+4$

Berechne die Schnittpunkte von $K_f$ mit den Koordinatenachsen.

$f\left(x\right)=\dfrac{x+1}{2x}$

$f\left(x\right)=\dfrac{\left(x-2\right)^2}{x+1}$

$f\left(x\right)=\dfrac{x^2-4}{x-1}$

$f\left(x\right)=\dfrac{\left(x+1\right)^2-3-x}{3x}$

Berechne die Schnittpunkte von $K_f$ mit den Koordinatenachsen.

$f\left(x\right)=\dfrac{\left(x+1\right)^2}{\left(x-1\right)^2}$

$f\left(x\right)=\dfrac{x^3+8}{2\left(x-1\right)}$

Berechne die Schnittpunkte von $K_f$ mit den Koordinatenachsen.

$f\left(x\right)=\mathrm e^x$

$f\left(x\right)=-\mathrm e^x+5$

$f\left(x\right)=\mathrm e^{2x+1}-\mathrm e^{9}$

$f\left(x\right)=2\mathrm e^{x+1}-2$

Berechne die Schnittpunkte von $K_f$ mit den Koordinatenachsen im angegebenen Intervall.

$f\left(x\right)=\sin{\left(x\right)}$ ; $-\pi\leq x\leq\pi$

$f\left(x\right)=\sin{\left(2x\right)}+1$ ; $-\pi\leq x\leq\pi$

$f\left(x\right)=2\cos{\left(x^2\right)}-8$ ; $-\pi\leq x\leq\pi$

$f\left(x\right)=\dfrac{1}{2}\cos{\left(x-\pi\right)}$ ; $-\pi\leq x\leq\pi$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Schnittpunkte mit den Koordinatenachsen berechnen

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse:

Setze den Funktionsterm der Funktion $f$ gleich Null und löse nach $x$ auf.

$\begin{array}{rll} f(x)&=&0\\ \left(x+2\right)^2&=&0&\scriptsize{ \mid\; \sqrt{\;}}\\ x+2&=&0&\scriptsize{ \mid\; -2}\\ x_{1,2}&=&-2 \\ \end{array}$

Daraus folgt der Punkt $P\left(-2\mid 0\right)$ .
Es handelt sich um eine doppelte Nullstelle.

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse:

Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.

$\begin{array}{rll} f\left(0\right)&=&\left(0+2\right)^2\\ f\left(0\right)&=&2^2\\ f\left(0\right)&=&4\\ \end{array}$

Daraus folgt der Punkt $Q\left(0\mid 4\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse:

Setze den Funktionsterm der Funktion $f$ gleich Null und löse nach $x$ auf.

$\begin{array}{rll} x^2-6x+5&=&0\\ \end{array}$

Vollständige Lösung anzeigen

$\boldsymbol{p}$ - $\boldsymbol{q}$ -Formel anwenden:

$\begin{array}{rll} x_{1,2} &=& 3\pm\sqrt {9-5}\\ &=&3\pm\sqrt{4}\\ &=&3\pm2\\ x_1&=&1\\ x_2&=&5\\ \end{array}$

Daraus folgen die Punkte $P_1\left(1\mid 0\right)$ und $P_2\left(5\mid 0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse:

Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.

$\begin{array}{rll} f\left(0\right)&=&-\left(0-1\right)^2+4\cdot0-4\\ &=&-\left(-1\right)^2-4\\ &=&-1-4\\ &=&-5\\ \end{array}$

Daraus folgt der Punkt $Q\left(0\mid -5\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse:

Setze den Funktionsterm der Funktion $f$ gleich Null und löse nach $x$ auf.

$\begin{array}{rll} x\left(x+3\right)^3&=&0\\ \end{array}$

Nach dem Satz vom Nullprodukt gilt, dass entweder der Term vor der Klammer oder die Klammer selbst gleich Null werden kann.

$\begin{array}{rll} x_1 &=&0\\ \end{array}$

$\begin{array}{rll} \left(x+3\right)^3&=&0&\scriptsize{\mid \sqrt[3]{\;}}\\ x+3&=&0&\quad\scriptsize{\mid -3}\\ x_{2}&=&-3\\ \end{array}$

Daraus folgen die Punkte $P_1\left(0\mid0\right)$ und $P_{2}\left(-3\mid0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse:

Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.

$\begin{array}{rll} f\left(0\right)&=&0\cdot\left(0+3\right)^3\\ &=&0\cdot\left(-3\right)^3\\ f\left(0\right)&=&0\\ \end{array}$

Daraus folgt der Punkt $Q\left(0\mid 0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse:

Setze den Funktionsterm der Funktion $f$ gleich Null und löse nach $x$ auf.

$\begin{array}{rll} x^2+1&=&0&\scriptsize{\mid -1}\\ x^2&=&-1&\scriptsize{\mid \sqrt{\;}}\\ x&=&\sqrt{-1}\\ \end{array}$

Für diese Gleichung gibt es keine Lösung, weil man aus einer negativen Zahl nicht die Wurzel ziehen kann.
Das Schaubild dieser Funktion hat also keine Schnittpunkte mit der $x$ -Achse.

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse:

Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.

$\begin{array}{rll} f\left(0\right)&=&0^2+1\\ f\left(0\right)&=&1\\ \end{array}$

Daraus folgt der Punkt $Q\left(0\mid 1\right)$ .

Schnittpunkte von $K_f$ mit den Koordinatenachsen berechnen

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse:

Setze den Funktionsterm der Fuktion $f$ gleich Null und löse nach $x$ auf.

$\begin{array}{rll} x^3+x^2-6x&=&0&\scriptsize{ x\; \text{auskl.}}\\ x\left(x^2+x-6\right)&=&0\\ \end{array}$

Nach dem Satz vom Nullprodukt gilt, dass entweder der Term vor der Klam- mer oder die Klammer selbst gleich Null werden kann.

$\begin{array}{rll} x_1&=&0\\ \end{array}$

$\begin{array}{rll} x^2+x-6&=&0\\ \end{array}$

$\boldsymbol{p}$ - $\boldsymbol{q}$ -Formel anwenden:

$\begin{array}{rll} x_{2,3}&=&-\dfrac{1}{2}\pm\sqrt{\dfrac{1}{4}+6}\\ &=&-\dfrac{1}{2}\pm\sqrt{6,25}\\ &=&-\dfrac{1}{2}\pm2,5\\ x_2&=&-3\\ x_3&=&2\\ \end{array}$

Daraus folgen die Punkte $P_1\left(-3\mid 0\right)$ ; $P_2\left(0\mid 0\right)$ ; $P_3\left(2\mid 0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse:

Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.

$\begin{array}{rll} f\left(0\right)&=&0^3+0^2-6\cdot0\\ f\left(0\right)&=&0\\ \end{array}$

Daraus folgt der Punkt $Q\left(0\mid0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse:

Setze den Funktionsterm der Funk- tion $f$ gleich Null und löse nach $x$ auf.

$\begin{array}{rll} x^4-5x^2+4&=&0&\scriptsize{ \text{Substitution:}\\\; z=x^2}\\ z^2-5z+4&=&0\\ \end{array}$

$\boldsymbol{p}$ - $\boldsymbol{q}$ -Formel anwenden:

$\begin{array}{rll} z_{1,2}&=&\dfrac{5}{2}\pm\sqrt{\dfrac{25}{4}-4}\\ &=&\dfrac{5}{2}\pm\sqrt{2,25}\\ &=&\dfrac{5}{2}\pm1,5\\ z_1&=&1\\ z_2&=&4\\ \end{array}$

Resubstitution:

$\begin{array}{rll} z_1&=&1\\ x_1^2&=&1&\quad\scriptsize{\mid \sqrt{\;}}\\ x_{1,2}&=&\pm1\\ \end{array}$

$\begin{array}{rll} z_2&=&4\\ x_2^2&=&4&\quad\scriptsize{\mid \sqrt{\;}}\\ x_{3,4}&=&\pm2\\ \end{array}$

Daraus folgen die Punkte $P_1\left(-2\mid0\right)$ ; $P_2\left(-1\mid 0\right)$ ; $P_3\left(1\mid 0\right)$ ; $P_4\left(2\mid 0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse:

Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.

$\begin{array}{rll} f\left(0\right)&=&0^4-5\cdot0^2+4\\ f\left(0\right)&=&4 \end{array}$

Daraus folgt der Punkt $Q\left(0\mid 4\right)$ .

Schnittpunkte von $K_f$ mit den Koordinatenachsen berechnen

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse:

Setze den Zähler gleich Null und löse $x$ auf:

$\begin{array}{rll} x+1&=&0&\scriptsize{\mid -1}\\ x&=&-1\\ \end{array}$

Daraus folgt der Punkt $P\left(-1\mid 0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse:

Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.

$\begin{array}{rll} f\left(0\right)&=&\dfrac{0+1}{2\cdot0}\\ &=&\dfrac{1}{0}\\ \end{array}$

Diese Gleichung hat keine Lösung, da man keine Zahl durch 0 teilen darf. Das Schaubild der Funktion besitzt somit keinen Schnittpunkt mit der $y$ -Achse.

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse:

Setze den Zähler gleich Null und löse $x$ auf:

$\begin{array}{rll} \left(x-2\right)^2&=&0&\scriptsize{\mid \sqrt{\;}}\\ x-2&=&0&\scriptsize{\mid +2}\\ x&=&2\\ \end{array}$

Daraus folgt der Punkt $P\left(2\mid 0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse:

Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.

$\begin{array}{rll} f\left(0\right)&=&\dfrac{\left(0-2\right)^2}{0+1}\\ &=&\dfrac{4}{1}\\ &=&4\\ \end{array}$

Daraus folgt der Punkt $Q\left(0\mid4\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse:

Setze den Zähler gleich Null und löse $x$ auf:

$\begin{array}{rll} x^2-4&=&0&\scriptsize{\mid -4}\\ x^2&=&4&\scriptsize{\mid \sqrt{\;}}\\ x_{1,2}&=&\pm2\\ \end{array}$

Daraus folgen die Punkte $P_1\left(-2\mid 0\right)$ und $P_2\left(2\mid 0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse:

Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.

$\begin{array}{rll} f\left(0\right)&=&\dfrac{0^2-4}{0-1}\\ &=&\dfrac{-4}{-1}\\ f\left(0\right)&=&4\\ \end{array}$

Daraus folgt der Punkt $Q\left(0\mid 4\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse:

Setze den Zähler gleich Null und löse $x$ auf:

$\begin{array}{rll} \left(x+1\right)^2-3-x&=&0& \end{array}$

Vollständige Lösung anzeigen

$\boldsymbol{p}$ - $\boldsymbol{q}$ -Formel anwenden:

$\begin{array}{rll} x_{1,2}&=&-\dfrac{1}{2}\pm\sqrt{\dfrac{1}{4}+2}\\ &=&-\dfrac{1}{2}\pm\sqrt{2,25}\\ &=&-\dfrac{1}{2}\pm1,5\\ x_1&=&-2\\ x_2&=&1\\ \end{array}$

Daraus folgen die Punkte $P_1\left(-2\mid 0\right)$ , $P_2\left(1\mid 0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse:

Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.

$\begin{array}{rll} f\left(0\right)&=&\dfrac{\left(0+1\right)^2-3-0}{3\cdot0}\\ &=&\dfrac{1-3}{0}\\ \end{array}$

Für diese Gleichung gibt es keine Lösung, weil keine Zahl durch 0 geteilt werden darf.
Das Schaubild dieser Funktion hat also keinen Schnittpunkt mit der $y$ -Achse.

Schnittpunkte von $K_f$ mit den Koordinatenachsen berechnen

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse:

Setze den Zähler gleich Null und löse $x$ auf:

$\begin{array}{rll} \left(x+1\right)^2&=&0&\scriptsize{\mid \sqrt{\;}}\\ x+1&=&0&\scriptsize{\mid -1}\\ x&=&-1\\ \end{array}$

Daraus folgt der Punkt $P\left(-1\mid 0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse:

Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.

$\begin{array}{rll} f\left(0\right)&=&\dfrac{\left(0+1\right)^2}{\left(0-1\right)^2}\\ &=&\dfrac{1}{1}\\ &=&1\\ \end{array}$

Daraus folgt der Punkt $Q\left(0\mid 1\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse:

Setze den Zähler gleich Null und löse $x$ auf:

$\begin{array}{rll} x^3+8&=&0&\scriptsize{\mid -8}\\ x^3&=&-8&\scriptsize{\mid \sqrt[3]{\;}}\\ x&=&-2\\ \end{array}$

Daraus folgt der Punkt $P\left(-2\mid 0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse:

Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.

$\begin{array}{rll} f\left(0\right)&=&\dfrac{0^3+8}{2\left(0-1\right)}\\ &=&\dfrac{8}{-2}\\ f\left(0\right)&=&-4\\ \end{array}$

Daraus folgt der Punkt $Q\left(0\mid-4\right)$ .

Schnittpunkte von $K_f$ mit den Koordinatenachsen berechnen

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse:

Setze den Funktionsterm von $f$ gleich Null und löse nach $x$ auf.

$\begin{array}{rll} \mathrm e^x&=&0&\scriptsize{\mid \ln{\left(\;\right)}}\\ \ln{\left(\mathrm e^x\right)}&=&\ln{\left(0\right)}\\ \end{array}$

Diese Gleichung hat keine Lösung, weil es für $\ln{\left(0\right)}$ keine Lösung gibt. Es gibt keine Zahl, mit der man $\mathrm e$ potenzieren kann, sodass das Ergebnis 0 ist.
Diese Funktion hat also keine Nullstellen.

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse:

Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.

$\begin{array}{rll} f\left(0\right)&=&\mathrm e^0\\ f\left(0\right)&=&1\\ \end{array}$

Daraus ergibt sicher der Punkt $Q\left(0\mid 1\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse:

Setze den Funktionsterm von $f$ gleich Null und löse nach $x$ auf.

$\begin{array}{rll} -\mathrm e^x+5&=&0&\scriptsize{\mid -5}\\ -\mathrm e^x&=&-5&\scriptsize{\mid \cdot\left(-1\right)}\\ \mathrm e^x&=&5&\scriptsize{\mid \ln{\left(\;\right)}}\\ \ln{\left(\mathrm e^x\right)}&=&\ln{\left(5\right)}\\ x&=&\ln{\left(5\right)}\\ \end{array}$

Daraus folgt der Punkt $P\left(\ln{\left(5\right)}\mid0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse:

Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.

$\begin{array}{rll} f\left(0\right)&=&-\mathrm e^0+5\\ &=&-1+5\\ f\left(0\right)&=&4\\ \end{array}$

Daraus folgt der Punkt $Q\left(0\mid4\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse:

Setze den Funktionsterm von $f$ gleich Null und löse nach $x$ auf.

$\begin{array}{rll} \mathrm e^{2x+1}-\mathrm e^{9}&=&0&\scriptsize{\mid +\mathrm e^9}\\ \mathrm e^{2x+1}&=&\mathrm e^{9}&\scriptsize{\mid \ln{\left(\;\right)}}\\ \ln{\left(\mathrm e^{2x+1}\right)}&=&\ln{\left(\mathrm e^{9}\right)}\\ 2x+1&=&9&\scriptsize{\mid -1}\\ 2x&=&8&\scriptsize{\mid :2}\\ x&=&4\\ \end{array}$

Daraus folgt der Punkt $P\left(4\mid0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse:

Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.

$\begin{array}{rll} f\left(0\right)&=&\mathrm e^{2\cdot0+1}-\mathrm e^9\\ &=&\mathrm e-\mathrm e^9\\ &\approx&-8100\\ \end{array}$

Daraus ergibt sich der Punkt $Q\left(0\mid-8100\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $x$ -Achse:

Setze den Funktionsterm der Funktion $f$ gleich Null und löse nach $x$ auf.

$\begin{array}{rll} 2\mathrm e^{x+1}-2&=&0&\scriptsize{\mid +2}\\ 2\mathrm e^{x+1}&=&2&\scriptsize{\mid :2}\\ \mathrm e^{x+1}&=&1&\scriptsize{\mid \ln{\left(\;\right)}}\\ \ln{\left(\mathrm e^{x+1}\right)}&=&\ln{\left(1\right)}\\ x+1&=&0&\scriptsize{\mid -1}\\ x&=&-1\\ \end{array}$

Daraus folgt der Punkt $P\left(-1\mid 0\right)$ .

$\blacktriangleright$ Schnittpunkt mit der $y$ -Achse:

Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.

$\begin{array}{rll} f\left(0\right)&=&2\mathrm e^{0+1}-2\\ f\left(0\right)&=&2\mathrm e-2\\ \end{array}$

Daraus ergibt sich der Punkt $Q\left(0\mid2\mathrm e-2\right)$ .

Schnittpunkte von $K_f$ mit den Koordinatenachsen im angegebenen Intervall berechnen

$>$ \blacktriangleright $</b> Schnittpunkt mit der$ x $-Achse: <div class="abstand_nueschrift"></div> Setze den Funktionsterm der Funktion$ f $gleich Null und löse nach$ x $auf. <div class="abstand_ntext"></div>$ \begin{array}{rll} \sin{\left(x\right)}&=&0\\ x_1&=&-\pi\\ x_2&=&0\\ x_3&=&\pi\\ \end{array} $<div class="abstand_ntext"></div> Daraus ergeben sich die Punkte$ P_1\left(-\pi\mid0\right) $,$ P_2\left(0\mid 0\right) $,$ P_3\left(\pi\mid 0\right)$.
$>$ \blacktriangleright $</b> Schnittpunkt mit der$ y$-Achse:
Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.
$\begin{array}{rll} f\left(0\right)&=&\sin{\left(0\right)}\\ f\left(0\right)&=&0\\ \end{array}$
Daraus ergibt sich der Punkt $Q\left(0\mid0\right)$ .

b)

$>$ \blacktriangleright $</b> Schnittpunkt mit der$ x $-Achse: <div class="abstand_ntext"></div> Setze den Funktionsterm der Funktion<span class="content mobile" style="clear:both"></span>$ f $gleich Null und löse nach$ x $auf. <div class="abstand_ntext"></div> <div class="content desktop">$ \begin{array}{rll} \sin{\left(2x\right)}+1&=&0&\scriptsize{\mid -1}\\ \sin{\left(2x\right)}&=&-1&\scriptsize{ \text{Substitution:}\; z=2x}\\ \sin{\left(z\right)}&=&-1\\ z_1&=&-\dfrac{\pi}{2}\\ z_{2}&=&\dfrac{3}{2}\pi\\ \end{array} $</div> <div class="content mobile"> <div class="content mobile" style="font-size:1.1em; text-indent:-3px !important"> <span style="vertical-align:middle">$ \begin{array}{rll} z_1&=&-\dfrac{\pi}{2}\\ z_{2}&=&\dfrac{3}{2}\pi\\ \end{array} $\(</span> <div class="showbox outer"> <div> <a style="text-align:left;width:140%;margin-right:900px;float:left;vertical-align:bottom" data-formula-id=$ Vollständige Lösung anzeigen

\)' class='mathjax-formula' src='https://mathjax.schullv.de/e787fd5765a0eaa6cc066e8522d6fc3e9fbe979a818e0c345bcb18227be34cdf?color=5a5a5a'/>\begin{array}{rll} \sin{\left(2x\right)}+1&=&0&\scriptsize{\mid -1}\\ \sin{\left(2x\right)}&=&-1&\scriptsize{ \text{Substitution:}\; z=2x}\\ \sin{\left(z\right)}&=&-1\\ z_1&=&-\dfrac{\pi}{2}\\ z_{2}&=&\dfrac{3}{2}\pi\\ \end{array} $</div> </div> </div> </div> <div style="clear:both"></div> <div class="abstand_ntext"></div> Resubstitution: <div class="abstand_ntext"></div>$ \begin{array}{rll} z_1&=&-\dfrac{\pi}{2}&\scriptsize{\mid z=2x}\\ 2x&=&-\dfrac{\pi}{2}&\scriptsize{\mid :2}\\ x_1&=&-\dfrac{\pi}{4}\\ \end{array}\begin{array}{rll} z_{2}&=&\dfrac{3}{2}\pi&\scriptsize{\mid z=2x}\\ 2x&=&\dfrac{3}{2}\pi&\scriptsize{\mid :2}\\ x_{2}&=&\dfrac{3}{4}\pi\\ \end{array} $<div style="clear:both"></div> <div class="abstand_ntext"></div> Daraus folgen die Punkte$ P_1\left(-\dfrac{\pi}{4}\mid 0\right) $und$ P_2\left(\dfrac{3}{4}\pi\mid 0\right)$.
$>$ \blacktriangleright $</b> Schnittpunkt mit der$ y$-Achse:
Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.
$\begin{array}{rll} f\left(0\right)&=&\sin{\left(2\cdot0\right)}+1\\ &=&0+1\\ f\left(0\right)&=&1\\ \end{array}$
Daraus folgt der Punkt $Q\left(0\mid1\right)$ .

c)

$>$ \blacktriangleright $</b> Schnittpunkt mit der$ x $-Achse: <div class="abstand_nueschrift"></div> Setze den Funktionsterm der Funktion$ f $gleich Null und löse nach$ x $auf. <div class="abstand_ntext"></div> <div class="content desktop">$ \begin{array}{rll} 2\cos{\left(x^2\right)}-8&=&0&\scriptsize{\mid +8}\\ 2\cos{\left(x^2\right)}&=&8&\scriptsize{\mid :2}\\ \cos{\left(x^2\right)}&=&4&\scriptsize{ \text{Substitution:}\; z=x^2}\\ \cos{\left(z\right)}&=&4\\ \end{array} $</div> <div class="content mobile"> <div class="content mobile" style="font-size:1.1em; text-indent:-3px !important"> <span style="vertical-align:middle">$ \begin{array}{rll} \cos{\left(z\right)}&=&4\\ \end{array} $$</span> <div class="showbox outer"> <div> <a style="text-align:left;width:140%;margin-right:900px;float:left;vertical-align:bottom" data-formula-id=$ Vollständige Lösung anzeigen

$' class='mathjax-formula' src='https://mathjax.schullv.de/caac3c39e83b4595085926364aacddd2c6c7efb9b312ec4cba19c9ad64927f85?color=5a5a5a'/>\begin{array}{rll} 2\cos{\left(x^2\right)}-8&=&0&\scriptsize{\mid +8}\\ 2\cos{\left(x^2\right)}&=&8&\scriptsize{\mid :2}\\ \cos{\left(x^2\right)}&=&4&\scriptsize{ \text{Substitution:}\; z=x^2}\\ \cos{\left(z\right)}&=&4\\ \end{array} $</div> </div> </div> </div> <div style="clear:both"></div> <div class="abstand_ntext"></div> Diese Gleichung hat keine Lösung, da$ \cos{\left(z\right)}$ niemals 4 wird, sondern höchstens 1.
Diese Funktion hat also keine Nullstellen.
$>$ \blacktriangleright $</b> Schnittpunkt mit der$ y$-Achse:
Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.
$\begin{array}{rll} f\left(0\right)&=&2\cos{\left(0^2\right)}-8\\ &=&2-8\\ &=&-6\\ \end{array}$
Daraus ergibt sich der Punkt $Q\left(0\mid-6\right)$ .

d)

$>$ \blacktriangleright $</b> Schnittpunkt mit der$ x $-Achse: <div class="abstand_nueschrift"></div> Setze den Funktionsterm der Funktion<span class="content mobile" style="clear:both"></span>$ f $gleich Null und löse nach$ x $auf. <div class="abstand_ntext"></div> <div class="content desktop">$ \begin{array}{rll} \dfrac{1}{2}\cos{\left(x-\pi\right)}&=&0&\scriptsize{\mid \cdot2}\\ \cos{\left(x-\pi\right)}&=&0&\scriptsize{ \text{Substitution:}\; \left(x-\pi\right)=z}\\ \cos{\left(z\right)}&=&0\\ z_1&=&-\dfrac{3}{2}\pi\\ z_2&=&-\dfrac{\pi}{2}\\ \end{array} $</div> <div class="content mobile"> <div class="content mobile" style="font-size:1.1em; text-indent:-3px !important"> <span style="vertical-align:middle">$ \begin{array}{rll} z_1&=&-\dfrac{3}{2}\pi\\ z_2&=&-\dfrac{\pi}{2}\\ \end{array} $$</span> <div class="showbox outer"> <div> <a style="text-align:left;width:140%;margin-right:900px;float:left;vertical-align:bottom" data-formula-id=$ Vollständige Lösung anzeigen

$' class='mathjax-formula' src='https://mathjax.schullv.de/0be291c71ab82939f78603d7397a11b2f6bf7c123f26f0888cce21a49aafe9ba?color=5a5a5a'/>\begin{array}{rll} \dfrac{1}{2}\cos{\left(x-\pi\right)}&=&0&\scriptsize{\mid \cdot2}\\ \cos{\left(x-\pi\right)}&=&0&\scriptsize{ \text{Substitution:}\; \left(x-\pi\right)=z}\\ \cos{\left(z\right)}&=&0\\ z_1&=&-\dfrac{3}{2}\pi\\ z_2&=&-\dfrac{\pi}{2}\\ \end{array} $</div> </div> </div> </div> <div style="clear:both"></div> <div class="abstand_ntext"></div> Resubstitution: <div class="abstand_ntext"></div>$ \begin{array}{rll} z_1&=&-\dfrac{3}{2}\pi&\scriptsize{\mid z=x-\pi}\\ x-\pi&=&-\dfrac{3}{2}\pi&\scriptsize{\mid +\pi}\\ x_1&=&-\dfrac{\pi}{2}\\ \end{array}\begin{array}{rll} z_2&=&-\dfrac{\pi}{2}&\scriptsize{\mid z=x-\pi}\\ x-\pi&=&-\dfrac{\pi}{2}&\scriptsize{\mid +\pi}\\ x_2&=&\dfrac{\pi}{2}\\ \end{array} $<div style="clear:both"></div> <div class="abstand_ntext"></div> Daraus folgen die Punkte$ P_1\left(-\dfrac{\pi}{2}\mid 0\right) $und$ P_2\left(\dfrac{\pi}{2}\mid 0\right)$.
$>$ \blacktriangleright $</b> Schnittpunkt mit der$ y$-Achse:
Um den Schnittpunkt mit der $y$ -Achse zu berechnen, setzt du $x=0$ in den Funktionsterm der Funktion $f$ ein.
$\begin{array}{rll} f\left(0\right)&=&\dfrac{1}{2}\cos{\left(0-\pi\right)}\\ f\left(0\right)&=&\dfrac{1}{2}\cdot(-1)\\ f(0)&=&-\dfrac{1}{2}\\ \end{array}$
Daraus ergibt sich der Punkt $Q\left(0\mid -\dfrac{1}{2}\right)$