Gerade - Gerade

Für die gegenseitige Lage von zwei Geraden gibt es vier Möglichkeiten:

Art der Lage	Anzahl gemeinsamer Punkte	Parallelität
identisch	$\infty$
sie schneiden sich	$1$
parallel aber nicht identisch	$0$
windschief	$0$

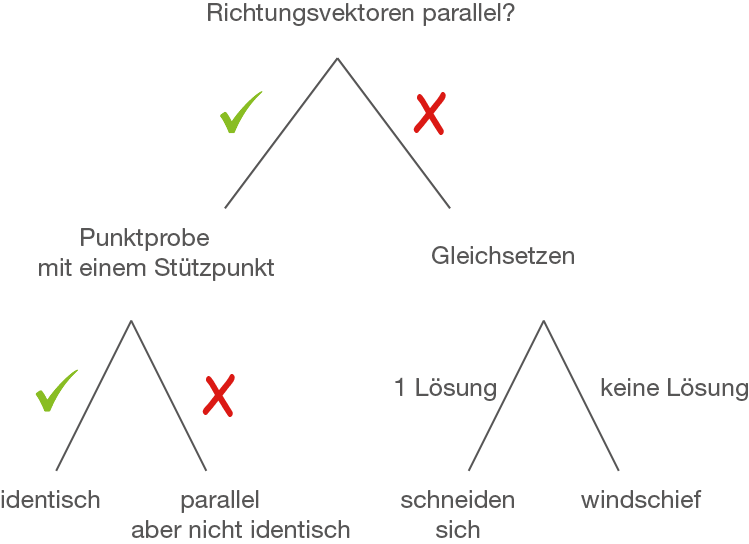
Vorgehen

Überprüfe die Geraden auf Parallelität. Überprüfe dazu, ob die beiden Richtungsvektoren linear abhängig sind.

Sind die Geraden parallel, so führe eine Punktprobe durch:
- Liegt der Stützpunkt der einen Gerade auch auf der anderen Gerade? Dann sind sie identisch
- Liegt der Stützpunkt der einen Gerade nicht auf der zweiten Gerade? Dann sind sie parallel aber nicht identisch

Sind sie nicht parallel, dann bestimme die Schnittpunkte der beiden Geraden durch Gleichsetzen.

Das LGS hat keine Lösung: Sie sind windschief.

Das LGS hat eine Lösung: Die Geraden schneiden sich.

Diagramm zur Prüfung der Parallelität von Richtungsvektoren mit verschiedenen Lösungsansätzen.

Untersuche die gegenseitige Lage der beiden Geraden.

$g:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} 1 \\ -2 \\ 1 \\ \end{array}} \right)+ r\left( {\begin{array}{*{20}r} -3 \\ 2 \\ 1 \\ \end{array}} \right)$

$h:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} 1 \\ -4 \\ 3 \\ \end{array}} \right)+ s\left( {\begin{array}{*{20}r} -2 \\ 1 \\ 1 \\ \end{array}} \right)$

$g:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} 4 \\ 5 \\ 1 \\ \end{array}} \right)+ r\left( {\begin{array}{*{20}r} 1 \\ 2 \\ 3 \\ \end{array}} \right)$

$h:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} 3 \\ 4 \\ 2 \\ \end{array}} \right)+ s\left( {\begin{array}{*{20}r} 5 \\ 9 \\ 8 \\ \end{array}} \right)$

$g:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} 2 \\ 5 \\ 1 \\ \end{array}} \right)+ r\left( {\begin{array}{*{20}r} 4 \\ 6 \\ 2 \\ \end{array}} \right)$

$h:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} -6 \\ 15 \\ 1 \\ \end{array}} \right)+ s\left( {\begin{array}{*{20}r} 2 \\ 3 \\ 1 \\ \end{array}} \right)$

$g:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} 4 \\ 3 \\ 1 \\ \end{array}} \right)+ r\left( {\begin{array}{*{20}r} 2 \\ 5 \\ 4 \\ \end{array}} \right)$

$h:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} 4 \\ 6 \\ 2 \\ \end{array}} \right)+ s\left( {\begin{array}{*{20}r} 6 \\ 15 \\ 12 \\ \end{array}} \right)$

$g:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} 2 \\ -5 \\ 1 \\ \end{array}} \right)+ r\left( {\begin{array}{*{20}r} 16 \\ 20 \\ 4 \\ \end{array}} \right)$

$h:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} -6 \\ -15 \\ -1 \\ \end{array}} \right)+ s\left( {\begin{array}{*{20}r} 4 \\ 5 \\ 1 \\ \end{array}} \right)$

$g:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} 3 \\ 2 \\ 1 \\ \end{array}} \right)+ r\left( {\begin{array}{*{20}r} 4 \\ 6 \\ 8 \\ \end{array}} \right)$

$h:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} 7 \\ 3 \\ 3 \\ \end{array}} \right)+ s\left( {\begin{array}{*{20}r} 0 \\ 5 \\ 6 \\ \end{array}} \right)$

Bestimme den Parameter $a$ so, dass die Geraden sich schneiden.

$g:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} 1 \\ 0 \\ 4 \\ \end{array}} \right)+ r\left( {\begin{array}{*{20}r} 4 \\ 0 \\ 1 \\ \end{array}} \right)$

$h:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} 7 \\ -1 \\ 1 \\ \end{array}} \right)+ s\left( {\begin{array}{*{20}r} 0 \\ 1 \\ 2a \\ \end{array}} \right)$

$g:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} 1 \\ 3 \\ 2 \\ \end{array}} \right)+ r\left( {\begin{array}{*{20}r} 8 \\ 2 \\ 2a \\ \end{array}} \right)$

$h:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} 4 \\ 6 \\ 3 \\ \end{array}} \right)+ s\left( {\begin{array}{*{20}r} 9 \\ 6 \\ 5 \\ \end{array}} \right)$

$g:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} 3 \\ 2 \\ 4 \\ \end{array}} \right)+ r\left( {\begin{array}{*{20}r} 4 \\ a \\ 7 \\ \end{array}} \right)$

$h:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} 4 \\ 3 \\ 2 \\ \end{array}} \right)+ s\left( {\begin{array}{*{20}r} 6 \\ 4 \\ 6 \\ \end{array}} \right)$

$g:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} 5 \\ 8 \\ 6 \\ \end{array}} \right)+ r\left( {\begin{array}{*{20}r} 7 \\ a \\ 2a \\ \end{array}} \right)$

$h:\;\overrightarrow{x} = \left( {\begin{array}{*{20}r} 4 \\ 3 \\ 2 \\ \end{array}} \right)+ s\left( {\begin{array}{*{20}r} 5 \\ 2 \\ 1 \\ \end{array}} \right)$

Zeige, dass die drei Geraden jeweils parallel zueinander sind.

$g:\overrightarrow{x}=\left(\begin{array}{r} 2\\ 7\\ 4\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 2\\ 1\\ -1\\ \end{array}\right)$

$i:\overrightarrow{x}=\left(\begin{array}{r} 2\\ 4\\ 0\\ \end{array}\right)+t\cdot\left(\begin{array}{r} 4\\ 2\\ -2\\ \end{array}\right)$

$h:\overrightarrow{x}=\left(\begin{array}{r} 0\\ 1\\ 2\\ \end{array}\right)+s\cdot\left(\begin{array}{r} -6\\ -3\\ 3\\ \end{array}\right)$

$g:\overrightarrow{x}=\left(\begin{array}{r} 1\\ 2\\ 3\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 15\\ -6\\ 9\\ \end{array}\right)$

$i:\overrightarrow{x}=\left(\begin{array}{r} 0\\ 4\\ 0\\ \end{array}\right)+t\cdot\left(\begin{array}{r} 10\\ -4\\ 6\\ \end{array}\right)$

$h:\overrightarrow{x}=\left(\begin{array}{r} -2\\ 3\\ 7\\ \end{array}\right)+s\cdot\left(\begin{array}{r} -5\\ 2\\ -3\\ \end{array}\right)$

$g:\overrightarrow{x}=\left(\begin{array}{r} -1\\ 1\\ 1\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 0\\ 4\\ 8\\ \end{array}\right)$

$i:\overrightarrow{x}=\left(\begin{array}{r} -3\\ 3\\ 3\\ \end{array}\right)+t\cdot\left(\begin{array}{r} 0\\ 3\\ 6\\ \end{array}\right)$

$h:\overrightarrow{x}=\left(\begin{array}{r} 2\\ -2\\ -2\\ \end{array}\right)+s\cdot\left(\begin{array}{r} 0\\ -1\\ -2\\ \end{array}\right)$

$g:\overrightarrow{x}=\left(\begin{array}{r} 3\\ 2\\ -4\\ \end{array}\right)+r\cdot\left(\begin{array}{r} -3\\ 2\\ 5\\ \end{array}\right)$

$i:\overrightarrow{x}=\left(\begin{array}{r} 1\\ 2\\ 3\\ \end{array}\right)+t\cdot\left(\begin{array}{r} 6\\ -4\\ -10\\ \end{array}\right)$

$h:\overrightarrow{x}=s\cdot\left(\begin{array}{r} -\frac{5}{2}\\ \frac{5}{3}\\ \frac{25}{6}\\ \end{array}\right)$

Bestimme $k$ so, dass die beiden Geraden parallel sind.

$g:\overrightarrow{x}=\left(\begin{array}{r} 1\\ 3\\ 1\\ \end{array}\right)+r\cdot\left(\begin{array}{r} k\\ 2\\ 4\\ \end{array}\right)$

$h:\overrightarrow{x}=\left(\begin{array}{r} 2\\ -1\\ 4\\ \end{array}\right)+s\cdot\left(\begin{array}{r} 3\\ 1\\ 2\\ \end{array}\right)$

$g:\overrightarrow{x}=\left(\begin{array}{r} -1\\ 5\\ 0\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 1\\ 2k\\ 2\\ \end{array}\right)$

$h:\overrightarrow{x}=\left(\begin{array}{r} 0\\ 2\\ 2\\ \end{array}\right)+s\cdot\left(\begin{array}{r} 3\\ 3\\ 6\\ \end{array}\right)$

$g:\overrightarrow{x}=\left(\begin{array}{r} -4\\ 1\\ 1\\ \end{array}\right)+r\cdot\left(\begin{array}{r} k\\ 2k\\ 9\\ \end{array}\right)$

$h:\overrightarrow{x}=\left(\begin{array}{r} 0\\ 0\\ 1\\ \end{array}\right)+s\cdot\left(\begin{array}{r} 2\\ 4\\ 6\\ \end{array}\right)$

$g:\overrightarrow{x}=\left(\begin{array}{r} 1\\ 0\\ -3\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 2\\ k\\ 0\\ \end{array}\right)$

$h:\overrightarrow{x}=\left(\begin{array}{r} 0\\ 2\\ 5\\ \end{array}\right)+s\cdot\left(\begin{array}{r} 1\\ 4\\ 0\\ \end{array}\right)$

Bestimme $m$ so, dass die beiden Geraden senkrecht aufeinander stehen.

$g:\overrightarrow{x}=\left(\begin{array}{r} 0\\ -1\\ 2\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 2\\ m\\ 1\\ \end{array}\right)$

$h:\overrightarrow{x}=\left(\begin{array}{r} -2\\ 1\\ 0\\ \end{array}\right)+s\cdot\left(\begin{array}{r} 1\\ -1\\ 1\\ \end{array}\right)$

$g:\overrightarrow{x}=\left(\begin{array}{r} -5\\ 4\\ 4\\ \end{array}\right)+r\cdot\left(\begin{array}{r} m\\ 1\\ 4\\ \end{array}\right)$

$h:\overrightarrow{x}=\left(\begin{array}{r} -1\\ 0\\ 2\\ \end{array}\right)+s\cdot\left(\begin{array}{r} 2\\ -2\\ -1\\ \end{array}\right)$

$g:\overrightarrow{x}=\left(\begin{array}{r} -6\\ 0\\ 4\\ \end{array}\right)+r\cdot\left(\begin{array}{r} m\\ 2m\\ 1\\ \end{array}\right)$

$h:\overrightarrow{x}=\left(\begin{array}{r} -2\\ 2\\ 0\\ \end{array}\right)+s\cdot\left(\begin{array}{r} 4\\ 2\\ -4\\ \end{array}\right)$

$g:\overrightarrow{x}=\left(\begin{array}{r} 0\\ 1\\ 0\\ \end{array}\right)+r\cdot\left(\begin{array}{r} 2\\ 1\\ -4\\ \end{array}\right)$

$h:\overrightarrow{x}=\left(\begin{array}{r} 4\\ 3\\ -8\\ \end{array}\right)+s\cdot\left(\begin{array}{r} m\\ -m\\ 1\\ \end{array}\right)$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Die Geraden können sich schneiden, parallel, identisch oder windschief sein.

$\begin{array}[t]{rll} \left( {\begin{array}{*{20}r} 1 \\ -2 \\ 1 \\ \end{array}} \right)+ r\left( {\begin{array}{*{20}r} -3 \\ 2 \\ 1 \\ \end{array}} \right)=\;... \end{array}$