Vermischte Aufgaben

Überprüfe, ob das Dreieck $ABC$ gleichschenklig oder gleichseitig ist.

$A(1\mid 2\mid 1),\;$ $B(2\mid 1\mid 1),\;$ $C(3\mid 3\mid 2)$

$A(1\mid -2\mid 2),\;$ $B(3\mid 2\mid 1),\;$ $C(3\mid 0\mid 3)$

$A(3\mid 0\mid 5),\;$ $B(3\mid 2\mid 3), \;$ $C(5\mid 0\mid 3)$

$A(0\mid 0\mid 6),\;$ $B(2\mid 0\mid 4), \;$ $C(4\mid 3\mid 8)$

$A(1\mid 1\mid 1),\;$ $B(2\mid 2\mid 2),\;$ $C(3\mid 3\mid 3)$

$A(2\mid 1\mid 1),\;$ $B(0\mid 3\mid 1),\;$ $C(0\mid 1\mid 3)$

Überprüfe, ob das Dreieck $ABC$ rechtwinklig ist.

$A(8\mid 3\mid 6)$ , $\;$ $B(2\mid 3\mid 4)$ , $\;$ $C(4\mid 3\mid 8)$

$A(1\mid -1\mid -2)$ , $\;$ $B(4\mid 2\mid -2)$ , $\;$ $C(2\mid 4\mid -2)$

$A(3\mid 0\mid 5),\;$ $B(3\mid 2\mid 3),\;$ $C(5\mid 0\mid 3)$

$A(1\mid 1\mid 1),\;$ $B (2\mid 3\mid 4),\;$ $C(0\mid 0\mid 2)$

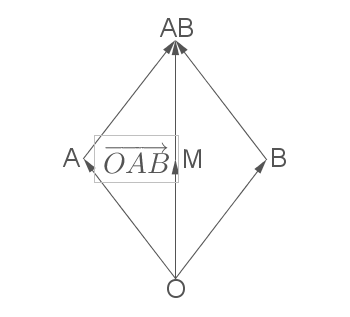
Berechne den Mittelpunkt $M$ der Strecke $AB$ .

$A(2\mid 4\mid 3), \;$ $B(0\mid -2\mid 5)$

$A(4\mid 5\mid -2), \;$ $B(2\mid 3\mid 6)$

Bestimme $B$ so, dass $M$ der Mittelpunkt der Strecke $AB$ ist.

$M(2\mid 5\mid 3),$ $A(1\mid 2\mid -3)$

$M(1\mid 3\mid -1),$ $A(2\mid 6\mid 1)$

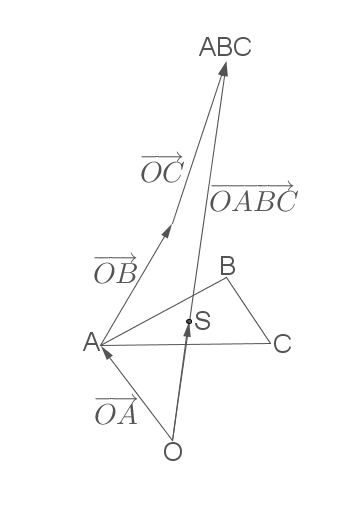
Bestimme den Schwerpunkt des Dreiecks $ABC.$

$A(1\mid 1\mid 5),$ $B(3\mid 1\mid 7),$ $C(5\mid 1\mid 3)$

$A(3\mid 4\mid 1),$ $B(0\mid 1\mid 3),$ $C(-3\mid 4\mid 5)$

Gegeben ist das Dreieck $ABC$ durch die Punkte $A(3\mid -3\mid 0)$ , $B(-4\mid -3\mid 0)$ und $C(-4\mid -3\mid 6)$ .
Weise nach, dass das Dreieck $ABC$ rechtwinklig ist und bestimme die Hypotenuse von $\Delta ABC$ , sowie dessen Flächeninhalt.

Betrachtet werden nun nur die Punkte $A$ und $B$ . Gemeinsam mit einem dritten Punkt $D$ , der in der
$x_1$ - $x_2$ -Ebene liegt, bilden sie ein Dreieck, das bei $B$ einen rechten Winkel hat und gleichschenklig ist. Es gibt zwei mögliche Punkte $D_1$ und $D_2$ , die diese Bedingung erfüllen. Berechnen Sie deren Koordinaten.

Gegeben ist das Dreieck mit den Punkten $A(1\mid 2\mid 0)$ , $B(-17\mid 8\mid -4)$ und $C(1\mid 4\mid 2)$ .

Zeige, dass das Dreieck gleichschenklig ist.

Wie müsste man einen Punkt $D$ wählen, sodass ein Parallelogramm entsteht?

Gegeben sind die Punkte $A(8\mid 2\mid 2)$ , $B(5\mid 2\mid 5)$ , $C(4\mid 6\mid 4)$ .
$A$ und $B$ und $C$ liegen in der Ebene $E$ .

Bestimme eine Koordinatengleichung von $E$ und die Schnittpunkte von $E$ mit den Koordinatenachsen.
Zeige, dass das Dreieck $ABC$ gleichschenklig und rechtwinklig ist.

In einem kartesischen Koordinatensystem sind die Punkte
$A(1\mid 2\mid 3)$ , $B(5\mid 0\mid -1)$ und $D(-1\mid 6\mid -1)$ gegeben.

Zeige, dass es einen Punkt $C$ gibt, für den das Viereck $ABCD$ ein Quadrat ist. Bestimme die Koordinaten von $C$ .

Das Quadrat $ABCD$ ist nun die Grundfläche einer Pyramide mit der Höhe $6$ LE. Der Fußpunkt der Pyramide ist der Mittelpunkt des Quadrates.
Bestimme die Koordinaten der beiden möglichen Pyramidenspitzen $S$ und $\(S$ .

10.

Drei Punkte $A$ , $B$ und $C$ liegen in einer Ebene, die nicht parallel zu einer der Koordinatenebenen verläuft.
Diese Punkte sollen drei der vier Eckpunkte der Grundfläche einer quadratischen Pyramide sein. Die Spitze der Pyramide befindet sich dabei senkrecht über dem Diagonalenschnittpunkt der quadratischen Grundfläche und ist 3 LE von diesem entfernt.
Beschreiben Sie ein Verfahren, um die Koordinaten der Spitze zu erhalten.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$A(1\mid 2\mid 1),\;$ $B(2\mid 1\mid 1),\;$ $C(3\mid 3\mid 2)$

$\overrightarrow{AB}$ = $\overrightarrow{OB}-\overrightarrow{OA}$ = $\begin{pmatrix} 2 - 0 \\ 1 - 0 \\ 1 - 0 \end{pmatrix}-\begin{pmatrix} 1 - 0 \\ 2 - 0 \\ 1 - 0 \end{pmatrix}$ = $\begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}-\begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix}$ = $\begin{pmatrix} 2 - 1 \\ 1 - 2 \\ 1 - 1 \end{pmatrix}$ = $\left(\begin{array}{r} 1 \\ -1 \\ 0 \end{array}\right)$

$\overrightarrow{AC}$ = $\overrightarrow{OC}-\overrightarrow{OA}$ = $\begin{pmatrix} 3 - 0 \\ 3 - 0 \\ 2 - 0 \end{pmatrix}-\begin{pmatrix} 1 - 0 \\ 2 - 0 \\ 1 - 0 \end{pmatrix}$ = $\begin{pmatrix} 3 \\ 3 \\ 2 \end{pmatrix}-\begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix}$ = $\begin{pmatrix} 3 - 1 \\ 3 - 2 \\ 2 - 1 \end{pmatrix}$ = $\begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}$

$\overrightarrow{BC}$ = $\overrightarrow{OC}-\overrightarrow{OB}$ = $\begin{pmatrix} 3 - 0 \\ 3 - 0 \\ 2 - 0 \end{pmatrix}-\begin{pmatrix} 2 - 0 \\ 1 - 0 \\ 1 - 0 \end{pmatrix}$ = $\begin{pmatrix} 3 \\ 3 \\ 2 \end{pmatrix}-\begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}$ = $\begin{pmatrix} 3 - 2 \\ 3 - 1 \\ 2 - 1 \end{pmatrix}$ = $\begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix}$

$\begin{array}{rlll} \overline{AB}&=\sqrt{2} \\[5pt] \overline{AC}&=\sqrt{6} \\[5pt] \overline{BC}&=\sqrt{6} \end{array}$

Vollständige Lösung anzeigen

Da $\overline{AC}=\overline{BC}=\sqrt{6}$ ist das Dreieck $ABC$ gleichschenklig.

$A(1\mid -2\mid 2), \;$ $B(3\mid 2\mid 1),\;$ $C(3\mid 0\mid 3)$

$\overrightarrow{AB}$ = $\left(\begin{array}{r} 2 \\ 4 \\ -1 \end{array}\right)$ $\quad$ $\overrightarrow{AC}$ = $\left(\begin{array}{r} 2 \\ 2 \\ 1 \end{array}\right)$ $\quad$ $\overrightarrow{BC}$ = $\left(\begin{array}{r} 0 \\ -2 \\ 2 \end{array}\right)$

$\begin{array}{rllll} \overline{AB}&=\sqrt{21} \\[5pt] \overline{AC}&=3 \\[5pt] \overline{BC}&=\sqrt{8} \end{array}$

Vollständige Lösung anzeigen

Da $\overline{AB}\neq\overline{AC}$ , $\overline{AC}\neq\overline{BC}$ und $\overline{BC}\neq\overline{AB}$ ist das Dreieck $ABC$ weder gleichschenklig noch gleichseitig.

$A(3\mid 0\mid 5),\;$ $B(3\mid 2\mid 3),\;$ $C(5\mid 0\mid 3)$

$\overrightarrow{AB}=\left(\begin{array}{r} 0 \\ 2 \\ -2 \end{array}\right)$ $\quad$ $\overrightarrow{AC}=\left(\begin{array}{r} 2 \\ 0 \\ -2 \end{array}\right)$ $\quad$ $\overrightarrow{BC}=\left(\begin{array}{r} 2 \\ -2 \\ 0 \end{array}\right)$

$\begin{array}{rlll} \overline{AB}&=\sqrt{8} \\[5pt] \overline{AC}&=\sqrt{8} \\[5pt] \overline{BC}&=\sqrt{8} \end{array}$

Vollständige Lösung anzeigen

Da $\overline{AB}=\overline{AC}=\overline{BC}=\sqrt{8}$ ist das Dreieck $ABC$ gleichseitig.

$A(0\mid 0\mid 6),\;$ $B(2\mid 0\mid 4),\;$ $C(4\mid 3\mid 8)$

$\overrightarrow{AB}=\left(\begin{array}{r} 2 \\ 0 \\ -2 \end{array}\right)$ $\quad$ $\overrightarrow{AC}=\left(\begin{array}{r} 4 \\ 3 \\ 2 \end{array}\right)$ $\quad$ $\overrightarrow{BC}=\left(\begin{array}{r} 2 \\ 3 \\ 4 \end{array}\right)$

$\begin{array}{rlll} \overline{AB}&=\sqrt{8} \\[5pt] \overline{AC}&=\sqrt{29} \\[5pt] \overline{BC}&=\sqrt{29} \end{array}$

Vollständige Lösung anzeigen

Da $\overline{AC}=\overline{BC}=\sqrt{29}$ ist das Dreieck $ABC$ gleichschenklig.

$A(1\mid 1\mid 1),\;$ $B(2\mid 2\mid 2),\;$ $C(3\mid 3\mid 3)$

$\overrightarrow{AB}$ = $\left(\begin{array}{r} 1 \\ 1 \\ 1 \end{array}\right)$ $\quad$ $\overrightarrow{AC}$ = $\left(\begin{array}{r} 2 \\ 2 \\ 2 \end{array}\right)$ $\quad$ $\overrightarrow{BC}$ = $\left(\begin{array}{r} 1 \\ 1 \\ 1 \end{array}\right)$

$\begin{array}{rlll} \overline{AB}&=\sqrt{3} \\[5pt] \overline{AC}&=\sqrt{12} \\[5pt] \overline{BC}&=\sqrt{3} \end{array}$

Vollständige Lösung anzeigen

Da $\overline{AB}=\overline{BC}=\sqrt{3}$ ist das Dreieck $ABC$ gleichschenklig.

$A(2\mid 1\mid 1),\;$ $B(0\mid 3\mid 1),\;$ $C(0\mid 1\mid 3)$

$\overrightarrow{AB}=\left(\begin{array}{r} -2 \\ 2 \\ 0 \end{array}\right)$ $\quad$ $\overrightarrow{AC}=\left(\begin{array}{r} -2 \\ 0 \\ 2 \end{array}\right)$ $\quad$ $\overrightarrow{BC}=\left(\begin{array}{r} 0 \\ -2 \\ 2 \end{array}\right)$

$\begin{array}{rlll} \overline{AB}&=\sqrt{8} \\[5pt] \overline{AC}&=\sqrt{8} \\[5pt] \overline{BC}&=\sqrt{8} \end{array}$

Vollständige Lösung anzeigen

Da $\overline{AB}=\overline{AC}$ = $\overline{BC}=\sqrt{8}$ ist das Dreieck $ABC$ gleichseitig.

$A(8\mid 3\mid 6),\;$ $B(2\mid 3\mid 4),\;$ $C(4\mid 3\mid 8)$

$\overrightarrow{AB}$ = $\left(\begin{array}{r} -6 \\ 0 \\ -2 \end{array}\right)$ $\quad$ $\overrightarrow{AC}$ = $\left(\begin{array}{r} -4 \\ 0 \\ 2 \end{array}\right)$ $\quad$ $\overrightarrow{BC}$ = $\left(\begin{array}{r} 2 \\ 0 \\ 4 \end{array}\right)$

$\begin{array}{rlll} \overrightarrow{AB}\cdot\overrightarrow{AC}&=20 \\[5pt] \overrightarrow{AB}\cdot\overrightarrow{BC}&=-20 \\[5pt] \overrightarrow{AC}\cdot\overrightarrow{BC}&=0 \end{array}$

Vollständige Lösung anzeigen

Da $\overrightarrow{AC}\cdot\overrightarrow{BC}=0$ stehen $\overrightarrow{AC}$ und $\overrightarrow{BC}$ senkrecht aufeinander und bei $C$ ist ein rechter Winkel.

$A(1\mid -1\mid -2)$ , $\; B(4\mid 2\mid -2)$ , $\; C(2\mid 4\mid -2)$

$\overrightarrow{AB}$ = $\left(\begin{array}{r} 3 \\ 3 \\ 0 \end{array}\right)$ $\quad$ $\overrightarrow{AC}$ = $\left(\begin{array}{r} 1 \\ 5 \\ 0 \end{array}\right)$ $\quad$ $\overrightarrow{BC}$ = $\left(\begin{array}{r} -2 \\ 2 \\ 0 \end{array}\right)$

$\begin{array}{rlll} \overrightarrow{AB}\cdot\overrightarrow{AC}&=18 \\[5pt] \overrightarrow{AB}\cdot\overrightarrow{BC}&=0 \\[5pt] \overrightarrow{AC}\cdot\overrightarrow{BC}&=8 \end{array}$

Vollständige Lösung anzeigen

Da $\overrightarrow{AB}\cdot\overrightarrow{BC}=0$ stehen $\overrightarrow{AB}$ und $\overrightarrow{BC}$ senkrecht aufeinander und bei $B$ ist ein rechter Winkel.

$A(3\mid 0\mid 5),\;$ $B(3\mid 2\mid 3),\;$ $C(5\mid 0\mid 3)$

$\overrightarrow{AB}$ = $\left(\begin{array}{r} 0 \\ 2 \\ -2 \end{array}\right)$ $\quad$ $\overrightarrow{AC}$ = $\left(\begin{array}{r} 2 \\ 0 \\ -2 \end{array}\right)$ $\quad$ $\overrightarrow{BC}$ = $\left(\begin{array}{r} 2 \\ -2 \\ 0 \end{array}\right)$

$\begin{array}{rlll} \overrightarrow{AB}\cdot\overrightarrow{AC}&=4 \\[5pt] \overrightarrow{AB}\cdot\overrightarrow{BC}&=-4 \\[5pt] \overrightarrow{AC}\cdot\overrightarrow{BC}&=4 \end{array}$

Vollständige Lösung anzeigen

Da $\overrightarrow{AB}\cdot\overrightarrow{AC}\neq\overrightarrow{AB}\cdot\overrightarrow{BC}\neq\overrightarrow{AC}\cdot\overrightarrow{BC}\neq 0$ hat das Dreieck $ABC$ keinen rechten Winkel.

$A(1\mid 1\mid 1),\;$ $B (2\mid 3\mid 4),\;$ $C(0\mid 0\mid 2)$

$\overrightarrow{AB}$ = $\left(\begin{array}{r} 1 \\ 2 \\ 3 \end{array}\right)$ $\quad$ $\overrightarrow{AC}$ = $\left(\begin{array}{r} -1 \\ -1 \\ 1 \end{array}\right)$ $\quad$ $\overrightarrow{BC}$ = $\left(\begin{array}{r} -2 \\ -3 \\ -2 \end{array}\right)$

$\begin{array}{rlll} \overrightarrow{AB}\cdot\overrightarrow{AC}=&=0 \\[5pt] \overrightarrow{AB}\cdot\overrightarrow{BC}&=-14 \\[5pt] \overrightarrow{AC}\cdot\overrightarrow{BC}&=3 \end{array}$

Vollständige Lösung anzeigen

Da $\overrightarrow{AB}\cdot\overrightarrow{AC}=0$ stehen $\overrightarrow{AB}$ und $\overrightarrow{AC}$ senkrecht aufeinander und bei $A$ ist ein rechter Winkel.

$A(2\mid 4\mid 3), \;$ $B(0\mid -2\mid 5)$

$M=\overrightarrow{OM}$ = $\dfrac{1}{2}\overrightarrow{OAB}$ = $\dfrac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})$ = $\dfrac{1}{2}\left(\left(\begin{array}{r} 2 \\ 4 \\ 3 \end{array}\right)+\left(\begin{array}{r} 0 \\ -2 \\ 5\end{array}\right)\right)$ = $\dfrac{1}{2}\left(\begin{array}{r} 2 \\ 2 \\ 8 \end{array}\right)$ = $\left(\begin{array}{r} 1 \\ 1 \\ 4 \end{array}\right)$

Diagramm eines geometrischen Problems mit Punkten A, B, O und M sowie der Linie AB.

$A(4\mid 5\mid -2), \;$ $B(2\mid 3\mid 6)$

$M=\dfrac{1}{2}\left(\left(\begin{array}{r} 4 \\ 5 \\ -2 \end{array}\right)+\left(\begin{array}{r} 2 \\ 3 \\ 6\end{array}\right)\right)$ = $\dfrac{1}{2}\left(\begin{array}{r} 6 \\ 8 \\ 4 \end{array}\right)$ = $\left(\begin{array}{r} 3 \\ 4 \\ 2 \end{array}\right)$

$M(2\mid 5\mid 3),\;$ $A(1\mid 2\mid -3)$

$\overrightarrow{OM}$ = $\dfrac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})$

$B=\overrightarrow{OB}$ = $2\overrightarrow{OM}-\overrightarrow{OA}=2\left(\begin{array}{r} 2 \\ 5 \\ 3 \end{array}\right)- \left(\begin{array}{r} 1 \\ 2 \\ -3 \end{array}\right)$ = $\left(\begin{array}{r} 4 \\ 10 \\ 6 \end{array}\right)- \left(\begin{array}{r} 1 \\ 2 \\ -3 \end{array}\right)$ = $\left(\begin{array}{r} 3 \\ 8 \\ 9 \end{array}\right)$

$M(1\mid 3\mid -1),$ $A(2\mid 6\mid 1)$

$B=2\left(\begin{array}{r} 1 \\ 3 \\ -1 \end{array}\right)- \left(\begin{array}{r} 2 \\ 6 \\ 1 \end{array}\right)$ = $\left(\begin{array}{r} 2 \\ 6 \\ -2 \end{array}\right)- \left(\begin{array}{r} 2 \\ 6 \\ 1 \end{array}\right)$ = $\left(\begin{array}{r} 0 \\ 0 \\ -3 \end{array}\right)$

$A(1\mid 1\mid 5),$ $B(3\mid 1\mid 7),$ $C(5\mid 1\mid 3)$

$\begin{array}{rll} S=&\overrightarrow{OS}\, =\, \dfrac{1}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}) \\[5pt] =& \dfrac{1}{3}\left(\left(\begin{array}{r} 1 \\ 1 \\ 5\end{array}\right)+\left(\begin{array}{r} 3 \\ 1 \\ 7\end{array}\right)+\left(\begin{array}{r} 5 \\ 1 \\ 3\end{array}\right)\right) \\[5pt] =&\dfrac{1}{3}\left(\begin{array}{r} 9 \\ 3 \\ 15\end{array}\right)\,=\,\left(\begin{array}{r} 3 \\ 1 \\ 5\end{array}\right) \end{array}$

Geometrische Darstellung von Vektoren und Punkten in einem Koordinatensystem.

$A(3\mid 4\mid 1),$ $B(0\mid 1\mid 3),$ $C(-3\mid 4\mid 5)$

$S=\dfrac{1}{3}\left(\left(\begin{array}{r} 3 \\ 4 \\ 1\end{array}\right)+\left(\begin{array}{r} 0 \\ 1 \\ 3\end{array}\right)+\left(\begin{array}{r} -3 \\ 4 \\ 5\end{array}\right)\right)$ = $\dfrac{1}{3}\left(\begin{array}{r} 0 \\ 9 \\ 9\end{array}\right)$ = $\left(\begin{array}{r} 0 \\ 3 \\ 3\end{array}\right)$

$A(3\mid -3\mid 0),$ $B(-4\mid -3\mid 0),$ $C(-4\mid -3\mid 6)$

$\blacktriangleright$ Nachweisen, dass $ABC$ rechtwinklig ist

1. Schritt: Aufstellen der Vektoren, die die Seiten des Dreiecks beschreiben

$\overrightarrow{AB}=\left( {\begin{array}{*{20}r} -4 \\ { - 3} \\ 0 \\ \end{array}} \right)-\left( {\begin{array}{*{20}r} 3 \\ { - 3} \\ 0 \\ \end{array}} \right)=\left( {\begin{array}{*{20}r} -7 \\ { 0} \\ 0 \\ \end{array}} \right)$

$\overrightarrow{AC}=\left( {\begin{array}{*{20}r} -4 \\ { - 3} \\ 6 \\ \end{array}} \right)-\left( {\begin{array}{*{20}r} 3 \\ { - 3} \\ 0 \\ \end{array}} \right)=\left( {\begin{array}{*{20}r} -7 \\ { 0} \\ 6 \\ \end{array}} \right)$

$\overrightarrow{BC}=\left( {\begin{array}{*{20}r} -4 \\ { - 3} \\ 6 \\ \end{array}} \right)-\left( {\begin{array}{*{20}r} -4 \\ { - 3} \\ 0 \\ \end{array}} \right)=\left( {\begin{array}{*{20}r} 0 \\ { 0} \\ 6 \\ \end{array}} \right)$

2. Schritt: Überprüfen auf rechte Winkel

$\overrightarrow{AB}\cdot\overrightarrow{AC}$ = $\left( {\begin{array}{*{20}r} -7 \\ { 0} \\ 0 \\ \end{array}} \right)\cdot\left( {\begin{array}{*{20}r} -7 \\ { 0} \\ 6 \\ \end{array}} \right)$ = $-7\cdot(-7)+ 0\cdot 0+0\cdot6$ = $49\neq0$

$\Rightarrow \scriptsize \text{kein rechter Winkel}$

$\overrightarrow{AB}\cdot\overrightarrow{BC}$ = $\left( {\begin{array}{*{20}r} -7 \\ { 0} \\ 0 \\ \end{array}} \right)\cdot\left( {\begin{array}{*{20}r} 0 \\ { 0} \\ 6 \\ \end{array}} \right)$ = $-7\cdot0+0\cdot 0+0\cdot6$ = $0$

$\Rightarrow \scriptsize \text{rechter Winkel}$

$\overrightarrow{AC}\cdot\overrightarrow{BC}$ = $\left( {\begin{array}{*{20}r} -7 \\ { 0} \\ 6 \\ \end{array}} \right)\cdot\left( {\begin{array}{*{20}r} 0 \\ { 0} \\ 6 \\ \end{array}} \right)$ = $-7\cdot0+0\cdot 0+6\cdot6$ = $36\neq0$

$\Rightarrow \scriptsize \text{kein rechter Winkel}$

3. Schritt: Bestimmung der Hypotenuse

Die Hypotenuse ist die Längste Seite des Dreiecks

$\overline{AB}=\left| \overrightarrow{AB}\right|$ = $\sqrt{(-7)^2+0^2+0^2}=7$

$\overline{AC}=\left| \overrightarrow{AC}\right|$ = $\sqrt{(-7)^2+0^2+6^2}=\sqrt{49+36}$ = $\sqrt{85}\approx9,22$

$\overline{BC}=\left| \overrightarrow{BC}\right|$ = $\sqrt{0^2+0^2+6^2}$ = $\sqrt{36}=6$

Somit ist $\overline{AC}$ die Hypotenuse.

4. Schritt: Bestimmung Flächeninhalt des rechtwinkligen Dreiecks

$A_{\Delta}=\dfrac{1}{2}\cdot 7\cdot6=21$ FE

$\blacktriangleright$ Bestimmung der Punkte $D_1$ und $D_2$

Da $D_{1,2}$ in der $x_1,x_2$ -Fläche liegen sollen, gilt für sie $D_{1,2}(x_1\mid x_2\mid 0)$ .

Es müssen zwei Bedingungen gelten:

$\overrightarrow{AB}\cdot\overrightarrow{BD_{1,2}}=0$ (Bedingung für rechtwinklig) und

$\left| \overrightarrow{AB}\right|$ = $\left| \overrightarrow{BD_{1,2}}\right|$ (Bedingung für gleichschenklig)

Bedingung für rechtwinklig

$\overrightarrow{BD_{1,2}}$ = $\left( {\begin{array}{*{20}r} x_1 \\ { x_2} \\ 0 \\ \end{array}} \right)-\left( {\begin{array}{*{20}r} -4 \\ { - 3} \\ 0 \\ \end{array}} \right)$ = $\left( {\begin{array}{*{20}r} x_1+4 \\ {x_2+3} \\ 0 \\ \end{array}} \right)$

$\begin{array}{rl} \overrightarrow{AB}\cdot\overrightarrow{BD_{1,2}}&=0 \end{array}$

Vollständige Lösung anzeigen

Aus $-28-7x_1=0$ folgt $-28=7x_1\;\Rightarrow\; x_1=-4$

Bedingung für gleichschenklig

$\left| \overrightarrow{AB}\right|$ = $\sqrt{(-7)^2}=7$ = $\left| \overrightarrow{BD_{1,2}}\right|$ = $\sqrt{(x_1+4)^2+(x_2+3)^2}$

mit $x_1=-4$ folgt

$\sqrt{(-4+4)^2+(x_2+3)^2}$ = $\sqrt{(x_2+3)^2}$ = $7$

$\sqrt{(x_2+3)^2}\\[5pt]$ wird genau dann $=7$ , wenn $(x_2+3)=\pm7$ ist.
Dies ist für $x_2=4$ und $x_2=-10$ der Fall.

Somit gibt es zwei mögliche Punkte $D_{1,2}$ , die die Bedingungen erfüllen.

$D_1(-4\mid 4\mid 0)$ und $D_2(-4\mid -10\mid 0)$ .

$A(1\mid 2\mid 0)$ , $B(-17\mid 8\mid -4)$ , $C(1\mid 4\mid 2)$

Bestimmen der Vektoren, die die Seiten des Dreiecks beschreiben:

$\overrightarrow{AB}$ = $\left( {\begin{array}{*{20}r} -17 \\ { 8} \\ -4 \\ \end{array}} \right)-\left( {\begin{array}{*{20}r} 1 \\ { 2} \\ 0 \\ \end{array}} \right)$ = $\left( {\begin{array}{*{20}r} -18 \\ { 6} \\ -4 \\ \end{array}} \right)$

$\overrightarrow{AC}$ = $\left( {\begin{array}{*{20}r} 1 \\ { 4} \\ 2 \\ \end{array}} \right)-\left( {\begin{array}{*{20}r} 1 \\ { 2} \\ 0 \\ \end{array}} \right)$ = $\left( {\begin{array}{*{20}r} 0 \\ { 2} \\ 2 \\ \end{array}} \right)$

$\overrightarrow{BC}$ = $\left( {\begin{array}{*{20}r} 1 \\ { 4} \\ 2 \\ \end{array}} \right)-\left( {\begin{array}{*{20}r} -17 \\ { 8} \\ -4 \\ \end{array}} \right)$ = $\left( {\begin{array}{*{20}r} 18 \\ { -4} \\ 6 \\ \end{array}} \right)$

Damit das Dreieck gleichschenklig ist müssen zwei Seiten gleich lang sein.

$\left|\overrightarrow{AB}\right|$ = $\sqrt{(-18)^2+6^2+(-4)^2}=\sqrt{376}$

$\left|\overrightarrow{AC}\right|$ = $\sqrt{0^2+2^2+2^2}=\sqrt{8}$

$\left|\overrightarrow{BC}\right|$ = $\sqrt{18^2+(-4)^2+6^2}=\sqrt{376}$

Somit sind $\overline{AB}$ und $\overline{BC}$ gleich lang und damit ist das Dreieck gleichschenklig.

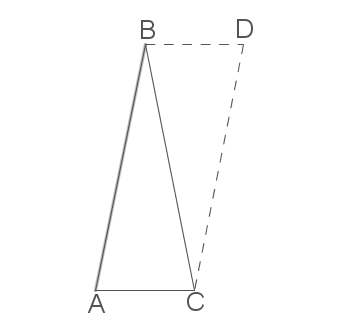
Bestimmung eines Punktes $D$

Für $D$ gilt zum Beispiel: $\overrightarrow{OA}+\overrightarrow{AC}+\overrightarrow{AB}$ .

$\overrightarrow{OD}$ = $\left(\begin{array}{r} 1\\ 2\\ 0\\ \end{array}\right)+\left( {\begin{array}{*{20}r} 0 \\ { 2} \\ 2 \\ \end{array}} \right)+\left( {\begin{array}{*{20}r} -18 \\ { 6} \\ -4 \\ \end{array}} \right)$ = $\left(\begin{array}{r} -17\\ 10\\ -2\\ \end{array}\right)$

$\;\Rightarrow\; D(-17\mid 10\mid -2)$

Es sind weitere Lösungen für den Punkt D möglich.

Geometrische Darstellung eines Dreiecks mit den Punkten A, B, C und D.

Gegeben sind die Punkte $A(8\mid 2\mid 2)$ , $B(5\mid 2\mid 5)$ , $C(4\mid 6\mid 4)$ .

$\blacktriangleright$ Bestimmung einer Koordinatengleichung von $E$

Da $A$ , $B$ und $C$ in der Ebene $E$ liegen bestimmt man über die Punkte zwei Spannvektoren der Ebene.

$\overrightarrow{AB}$ = $\left(\begin{array}{r} 5\\ 2\\ 5\\ \end{array}\right)-\left(\begin{array}{r} 8\\ 2\\ 2\\ \end{array}\right)$ = $\left(\begin{array}{r} -3\\ 0\\ 3\\ \end{array}\right)$

$\overrightarrow{AC}$ = $\left(\begin{array}{r} 4\\ 6\\ 4\\ \end{array}\right)-\left(\begin{array}{r} 8\\ 2\\ 2\\ \end{array}\right)$ = $\left(\begin{array}{r} -4\\ 4\\ 2\\ \end{array}\right)$

Mit $\overrightarrow{OA}$ als Stützvektor ergibt sich die Parameterform von $E$ mit

$E$ : $\overrightarrow{x}$ = $\left(\begin{array}{r} 8\\ 2\\ 2\\ \end{array}\right)+s\cdot\left(\begin{array}{r} -3\\ 0\\ 3\\ \end{array}\right)+t\cdot\left(\begin{array}{r} -4\\ 4\\ 2\\ \end{array}\right)$ $\quad s,t\in\mathbb{R}$

Für die Koordinatenform von $E$ braucht man einen Normalenvektor $\overrightarrow{n}$ von $E$

$\blacktriangleright$ Berechnung eines Normalenvektors von $E$ mit dem Kreuzprodukt (Formel s. Skript)

$\left(\begin{array}{r} -3\\ 0\\ 3\\ \end{array}\right)\times\left(\begin{array}{r} -4\\ 4\\ 2\\ \end{array}\right)$ = $\left(\begin{array}{r} 0\cdot2-4\cdot3\\ 3\cdot(-4)-2\cdot(-3)\\ -3\cdot4-(-4)\cdot0\\ \end{array}\right)$ = $\left(\begin{array}{r} -12\\ -6\\ -12\ \end{array}\right)$ = $-6\cdot\left(\begin{array}{r} 2\\ 1\\ 2\\ \end{array}\right)$

Vorläufige Koordinatengleichung von $E$

$E$ : $2x_1+x_2+2x_3=d$

Einsetzen des Punktes $A(8\mid 2\mid 2)$ liefert

$E$ : $2\cdot8+2+2\cdot2=22=d$

$\Rightarrow\;\;2x_1+x_2+2x_3=22$

$\blacktriangleright$ Berechnung der Schnittpunkte $E$ mit den Koordinatenachsen (Spurpunkte)

Für den Schnittpunkte mit der $x_1$ -Achse gilt $x_2=0$ und $x_3=0$

$2x_1+0+2\cdot0=22$ $\Rightarrow\;x_1=11$ $\Rightarrow S_1(11\mid 0\mid 0)$

Für den Schnittpunkte mit der $x_2$ -Achse gilt $x_1=0$ und $x_3=0$

$2\cdot0+x_2+2\cdot0=22$ $\Rightarrow\;x_2=22$ $\Rightarrow S_2(0\mid 22\mid 0)$

Für den Schnittpunkte mit der $x_3$ -Achse gilt $x_1=0$ und $x_2=0$

$2\cdot0+0+2\cdot x_3=22$ $\Rightarrow\;x_3=11$ $\Rightarrow S_3(0\mid 0\mid 11)$

$\blacktriangleright$ Nachweis, dass das Dreieck $ABC$ gleichschenklig ist

Ein Dreieck ist gleichschenklig, wenn zwei Seiten gleich lang sind.

$\begin{array}{rlll} \overrightarrow{AB}=&\left(\begin{array}{r} -3\\ 0\\ 3\\ \end{array}\right) \left|\overrightarrow{AB}\right|&=\sqrt{18} \\[5pt] \overrightarrow{AC}=&\left(\begin{array}{r} -4\\ 4\\ 2\\ \end{array}\right) \left|\overrightarrow{AC}\right|&=6 \\[5pt] \overrightarrow{BC}=&\left(\begin{array}{r} -1\\ 4\\ -1\\ \end{array}\right) \left|\overrightarrow{BC}\right|&=\sqrt{18} \end{array}$

Vollständige Lösung anzeigen

Damit gilt $\left|\overrightarrow{BC}\right|$ = $\left|\overrightarrow{AB}\right|$ = $\sqrt{18}$ . Das Dreieck $ABC$ ist somit gleichschenklig.

$\blacktriangleright$ Nachweis, dass das Dreieck $ABC$ rechtwinklig ist

Zeige, dass zwei der drei Dreiecksseiten einen rechten Winkel einschließen. Dies ist der Fall, wenn ihr Skalarprodukt den Wert Null annimmt.

Behauptung: Die Vektoren $\overrightarrow{AB}$ und $\overrightarrow{BC}$ schließen im Punkt $B$ einen rechten Winkel ein.

$\overrightarrow{AB}\circ\overrightarrow{BC}=$ $\begin{pmatrix}-3\\0\\3\end{pmatrix}\circ\begin{pmatrix}-1\\4\\-1\end{pmatrix}$ = $-3\cdot(-1)+0\cdot4+3\cdot(-1)$ $=3-3=0$

Das Dreieck $ABC$ ist somit rechtwinklig.

Die Punkte $A(1\mid 2\mid 3)$ , $B(5\mid 0\mid -1)$ und $D(-1\mid 6\mid -1)$ bilden ein gleichschenkliges rechtwinkliges Dreieck. Die Vektoren, die die Seiten dieses Dreiecks beschreiben lauten

$\overrightarrow{AB}$ = $\left(\begin{array}{r} 4\\ -2\\ -4\\ \end{array}\right)$ $\quad\overrightarrow{AD}$ = $\left(\begin{array}{r} -2\\ 4\\ -4\\ \end{array}\right)$ $\quad\overrightarrow{BD}$ = $\left(\begin{array}{r} -6\\ 6\\ 0\\ \end{array}\right)$

Es gilt

$\overrightarrow{AB}\circ\overrightarrow{AD}$ = $\left(\begin{array}{r} 4\\ -2\\ -4\\ \end{array}\right)\circ\left(\begin{array}{r} -2\\ 4\\ -4\\ \end{array}\right)=0$

$\left|\overrightarrow{AB}\right|$ = $\sqrt{4^2+(-2)^2+(-4)^2}$ = $\sqrt{36}$ $=6$ $=\left|\overrightarrow{AD}\right|$

Der Punkt $C$ soll nun die drei Punkte zu einem Quadrat ergänzen.

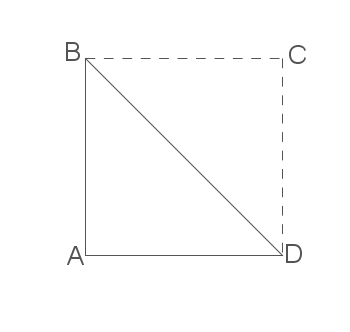Diagramm eines Rechtecks mit Punkten A, B, C und D sowie einer diagonalen Linie.

Es muss gelten

$\overrightarrow{OC}$ = $\overrightarrow{OB}+\overrightarrow{AD}$ = $\left(\begin{array}{r} 5\\ 0\\ -1\\ \end{array}\right)+\left(\begin{array}{r} -2\\ 4\\ -4\\ \end{array}\right)$ = $\left(\begin{array}{r} 3\\ 4\\ -5\\ \end{array}\right)\;\;\Rightarrow\;\;C(3\mid 4\mid -5)$

Der Mittelpunkt $M$ des Quadrates ist der Mittelpunkt der Strecke $\overline{BD}$

$\overrightarrow{OM}$ = $\overrightarrow{OB}+\dfrac{1}{2}\overrightarrow{BD}$ = $\left(\begin{array}{r} 5\\ 0\\ -1\\ \end{array}\right)+\dfrac{1}{2}\cdot\left(\begin{array}{r} -6\\ 6\\ 0\\ \end{array}\right)$ = $\left(\begin{array}{r} 2\\ 3\\ -1\\ \end{array}\right)\;\;\Rightarrow\;\;M(2\mid 3\mid -1)$

Berechnung der Punkte $S$ und $\(S$

Die Punkte $S$ und $\(S$ haben den Abstand $6$ LE zu der Ebene $H$ , in der das Quadrat liegt.

Bestimmung einer Koordinatengleichung von $H$ :

$\begin{array}[t]{rll} \text{I}&\overrightarrow{n}\circ\overrightarrow{AB}=... \\[5pt] \text{II}&\overrightarrow{n}\circ\overrightarrow{AD}=... \\[5pt]\hline \end{array}$

Vollständige Lösung anzeigen

Wählt man $n_1=2$ so ergibt sich $n_2=2$ und $n_3=1$ (eingesetzt in Ⅰ).

Es ergibt sich die vorläufige Koordinatenform von $H$ mit $H$ : $2x+2y+z=d$ .

Setzt man den Punkt $B$ der auf $H$ liegt in die Koordinatengleichung ein, so ergibt sich

$2\cdot5+2\cdot0-1=9$ $\Rightarrow\;$ $H$ : $2x+2y+z=9$

Ein Normaleneinheitsvektor (Länge $=1$ LE) der Ebene $H$ ist:

$\overrightarrow{n_0}$ = $\dfrac{1}{\sqrt{2^2+2^2+1^2}}\cdot\left(\begin{array}{r} 2\\ 2\\ 1\\ \end{array}\right)$ = $\dfrac{1}{3}\cdot\left(\begin{array}{r} 2\\ 2\\ 1\\ \end{array}\right)$

Für eine Pyramide mit dem Quadrat $ABCD$ als Grundfläche und der Höhe $6$ ergeben sich somit als mögliche Pyramidenspitzen

$\overrightarrow{OS}$ = $\overrightarrow{OM}+6\cdot\overrightarrow{n_0}$ = $\left(\begin{array}{r} 2\\ 3\\ -1\\ \end{array}\right)+\dfrac{1}{3}\cdot6\cdot\left(\begin{array}{r} 2\\ 2\\ 1\\ \end{array}\right)$ = $\left(\begin{array}{r} 6\\ 7\\ 1\\ \end{array}\right)\;\Rightarrow\;S(6\mid 7\mid 1)$

$\overrightarrow{OS}$ = $\overrightarrow{OM}-6\cdot\overrightarrow{n_0}$ = $\left(\begin{array}{r} 2\\ 3\\ -1\\ \end{array}\right)-\dfrac{1}{3}\cdot6\cdot\left(\begin{array}{r} 2\\ 2\\ 1\\ \end{array}\right)$ = $\left(\begin{array}{r} -2\\ -1\\ -3\\ \end{array}\right)\;\Rightarrow\;S(-2\mid -1\mid -3)$

10.

Um die Spitze der Pyramide zu berechnen, sollten die folgenden Schritte gemacht werden:

Die drei Eckpunkte der quadratischen Grundfläche werden mit einem vierten Punkt $D$ zu einem Quadrat ergänzt. $D$ ergibt sich dabei aus einer Vektorkette der anderen Punkte.
Der Diagonalenschnittpunkt $M$ dieses Quadrates wird ebenfalls mit einer Vektorkette bestimmt.
Von der Ebene $E$ wird der Normalenvektor gebildet und daraus der Normaleneinheitsvektor (Vektor mit derselben Richtung, aber einer Länge von genau 1) gebildet.
Mithilfe des Normaleneinheitsvektors wird vom Punkt $M$ aus drei Schritte nach oben gegangen. Durch diese Vektorkette ergeben sich letztlich die Koordinaten der Pyramidenspitze $S$ .

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?