Maximaler Umfang

Einführung

Bei Extremwertaufgaben mit Nebenbedingung benötigst du eine Zielfunktion, die du minimieren bzw. maximieren kannst.

Gehe folgendermaßen vor:

Fertige eine Skizze an.

Suche die Größe, die minimal bzw. maximal werden soll. Das ist hier der Umfang, schreibe die geometrische Formel dieses Umfangs auf.

Stelle die Nebenbedingung auf. Überlege dir wie die Variablen der gesuchten Größe zusammenhängen.
Falls ein entscheidender Punkt im Koordinatensystem auf dem Graphen liegt, schreibe ihn mit Hilfe des Funktionsterms des Graphen.

Bilde nun die Zielfunktion, indem du die Nebenbedingung nach einer der Variablen auflöst und in den Term für die extremale Größe einsetzt. Vereinfache diesen Term so weit wie möglich und bestimme den Definitionsbereich der Zielfunktion.

Bestimme die absoluten Extremstellen der Zielfunktion. Vergiss dabei nicht, zu überprüfen, ob diese Kandidaten auch relative Extremstellen sind. Außerdem muss überprüft werden, ob an den Randstellen des Definitionsbereichs noch kleinere/größere Werte für die extremale Größe auftreten.

Stelle nun die Verbindung zur Aufgabenstellung her, indem du die zweite Variable und den Extremwert berechnest.

Beispiel mit Lösungsskizze

Gegeben ist die Funktion $f (x) = - x^2 + 4$ . Das Schaubild der Funktion $f$ schließt mit den Koordinatenachsen eine Fläche ein. In dieser Fläche soll ein Rechteck mit maximalem Umfang konstruiert werden. Das Rechteck liegt mit einer Kante auf der $x$ -Achse, mit einer anderen auf der $y$ -Achse.

Skizze

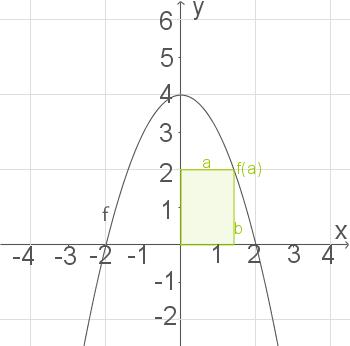
Größe, die maximal werden soll:
$U=2(a+b)$

Nebenbedingung:
$b=f(a)=-a^2+4$

Zielfunktion:
$U(a) =2(a+f(a))$ = $2(a+(-a^2 + 4))$ = $-2a^2 + 2a +8$ mit Definitionsbereich $\mathbb{D} = [0,2]$ .

Bestimme die absoluten Extremstellen der Zielfunktion.
$U(a) =-2a^2 + 2a +8$
$U‘(a) =-4a + 2$
$U‘‘(a) =-4$
$\begin{array}[t]{rll} U‘(a)&=&0 \\[5pt] 0&=&-4a + 2\\[5pt] a&=&0,5 \end{array}$
$U‘‘(0,5) =-4\lt 0$ es handelt sich also um ein Maximum.
Der maximale Wert ist somit: $U(0,5) = 8,5$
Überprüfen der Randstellen:
$U(0)$ = $8 \lt 8,5$
$U(2)$ = $(-2) \cdot 4 + 4 +8$ = $4 \lt 8,5$

Für die Seite $b$ gilt dann: $b = -0,5^2 + 4 = 3,75$ .
Der maximale Umfang beträgt somit $8,5$ .

Den maximalen Umfang bestimmen

Zunächst muss eine Funktion entwickelt werden, mit der wir den Umfang eines solchen Rechtecks berechnen können. Hierfür verdeutlichen wir uns die Aufgabe noch einmal mit Hilfe einer Skizze (das eingezeichnete Rechteck ist nicht das ideale, sondern ein beliebiges!):

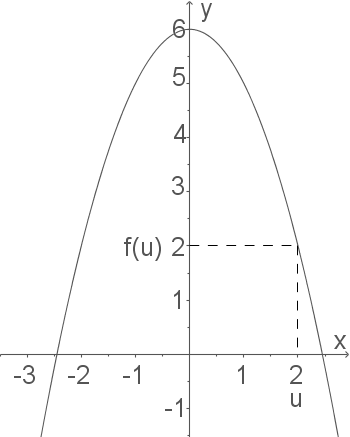Graf einer Parabel mit dem Scheitelpunkt bei (0, 6) und der x-Achse von -3 bis 2.

Die Kantenlängen des Rechtecks haben also die Länge $u$ und $f\left(u\right)$ .
Der Umfang berechnet sich immer dadurch, dass man die Längen aller Kanten addiert. In diesem Fall wäre der Umfang also:

$U\left(u\right)=2\cdot u+2\cdot f\left(u\right)$

Mit dieser Funktionsgleichung, die uns den Umfang in Abhängigkeit von $u$ angibt, können wir nun weiter rechnen und die Werte einsetzen:

$\begin{array}[t]{rll} U\left(u\right)=&2u+2\left(-u^2+6\right)\\ =&2u-2u^2+12\\ U\left(u\right)=&-2u^2+2u+12 \end{array}$

Um den maximalen Umfang zu berechnen, wird nun die Maximalstelle dieser Umfangsfunktion bestimmt:

$\begin{array}[t]{rll} U\left(u\right)=&-2u^2+2u+12\\ U‘\left(u\right)=&-4u+2\\ U‘‘\left(u\right)=&-4 \end{array}$

Maximalstelle berechnen über Nullstellen der ersten Ableitungsfunktion:

$\begin{array}[t]{rll} U‘\left(u\right)=&0\\ -4u+2=&0&\quad\mid\;-2\\ -4u=&-2&\quad\mid\;:\left(-4\right)\\ u=&\dfrac{1}{2} \end{array}$

Überprüfen der hinreichenden Bedingung:

$\begin{array}[t]{rll} f‘‘\left(\dfrac{1}{2}\right)=-4& <0:\;\small{\text{Maximum}} \end{array}$

Für $u=\dfrac{1}{2}$ wird der Umfang des Rechtecks also maximal. Den Umfang selbst liefert uns die Umfangfunktion:

$U\left(\dfrac{1}{2}\right)=12,5$

Vollständige Lösung anzeigen

Der maximale Umfang des Rechtecks beträgt $12,5$ LE.

Den maximalen Umfang bestimmen

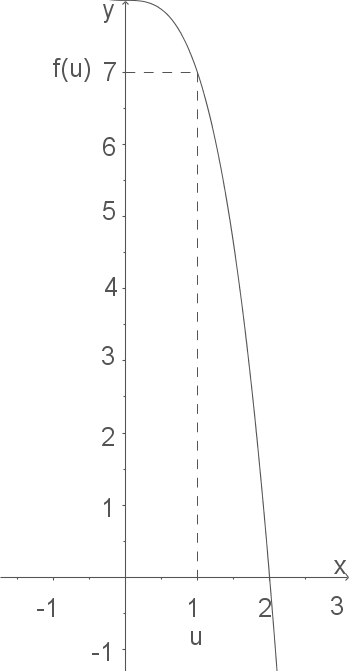Graph einer mathematischen Funktion mit Achsenbeschriftung und asymptotischem Verhalten.

$U\left(u\right)=2\cdot u+2\cdot f\left(u\right)$ wird zu:

$\begin{array}[t]{rll} U\left(u\right)=&2u+2\left(-u^3+8\right)\\ =&2u-2u^3+16\\ U\left(u\right)=&-2u^3+2u+16 \end{array}$

Um den maximalen Umfang zu berechnen, werden nun die Maximalstellen dieser Umfangsfunktion bestimmt:

$\begin{array}[t]{rll} U\left(u\right)=&-2u^3+2u+16\\ U‘\left(u\right)=&-6u^2+2\\ U‘‘\left(u\right)=&-12u \end{array}$

Maximalstelle bestimmen:

$\begin{array}[t]{rll} U‘\left(u\right)=&0\\ -6u^2+2=&0&\quad\mid\;-2\\ -6u^2=&-2&\quad\mid\;:\left(-6\right)\\ u^2=&\dfrac{1}{3}&\quad\mid\;\sqrt{\;}\\ u_{1,2}=&\pm\sqrt{\dfrac{1}{3}} \end{array}$

Überprüfen der hinreichenden Bedingung:

$f‘‘\left(\scriptsize{-\sqrt{\dfrac{1}{3}}}\right)=-12\cdot\left(\scriptsize{-\sqrt{\dfrac{1}{3}}}\right) >0$

Vollständige Lösung anzeigen

Für $u=\sqrt{\dfrac{1}{3}}$ wird der Umfang des Rechtecks also maximal. Den Umfang selbst liefert uns die Umfangfunktion:

$U\left(\sqrt{\dfrac{1}{3}}\right)\approx16,77$

Vollständige Lösung anzeigen

Der maximale Umfang des Rechtecks beträgt $16,77$ LE.

Den maximalen Umfang bestimmen

Nullstellen von $f$ bestimmen:

$\begin{array}[t]{rll} f\left(x\right)=&0\\ -x^2+4=&0&\quad\mid\;-4\\ -x^2=&-4&\quad\mid\;\cdot\left(-1\right)\\ x^2=&4&\quad\mid\;\sqrt{\;}\\ x_{1,2}=&\pm2 \end{array}$

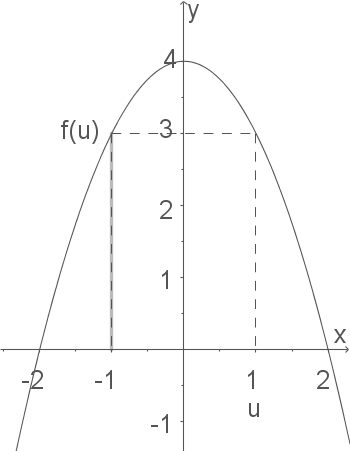Graf einer Parabel mit Achsenbeschriftung und Markierungen für Werte auf der y-Achse.

Die Länge der Grundkante wäre in diesem Falle also $2u$ , die Längen der anderen Kante jeweils $f\left(u\right)$ . Der Umfang eines Rechtecks berechnet sich immer, indem alle Kantenlängen addiert werden, in diesem Falle also:

$\begin{array}[t]{rll} U\left(u\right)&=& 2\cdot 2u+2\cdot f\left(u\right)\\[5pt] U\left(u\right)&=& 4u+2\cdot f\left(u\right) \end{array}$

Mit dieser Funktionsgleichung, die uns den Umfang in Abhängigkeit von $u$ angibt, können wir nun weiter rechnen und die Werte einsetzen:

$\begin{array}[t]{rll} U\left(u\right)=&4u+2\left(-u^2+4\right)\\ =&4u-2u^2+8\\ U\left(u\right)=&-2u^2+4u+8 \end{array}$

Um den maximalen Umfang zu berechnen, wird nun die Maximalstelle dieser Umfangsfunktion bestimmt:

$\begin{array}[t]{rll} U\left(u\right)=&-2u^2+4u+8\\ U‘\left(u\right)=&-4u+4\\ U‘‘\left(u\right)=&-4 \end{array}$

Extremstellen bestimmen:

$\begin{array}[t]{rll} U‘\left(u\right)=&0\\ -4u+4=&0&\quad\mid\;-4\\ -4u=&-4&\quad\mid\;:\left(-4\right)\\ u=&1 \end{array}$

Überprüfen der hinreichenden Bedingung:

$\begin{array}[t]{rll} f‘‘\left(1\right)=&-4 &\lt 0:\;\small{\text{Maximum}} \end{array}$

Für $u=1$ wird der Umfang des Rechtecks also maximal. Den Umfang selbst liefert uns die Umfangfunktion:

$\begin{array}[t]{rll} U\left(1\right)=&-2\cdot1^2+4\cdot1+8\\ =&-2+4+8\\ U\left(1\right)=&10 \end{array}$

Der maximale Umfang des Rechtecks beträgt $10$ LE.

Den maximalen Umfang bestimmen

Auch, wenn wir keine genaue Vorstellung des Schaubilds haben, skizzieren wir das Szenario kurz:

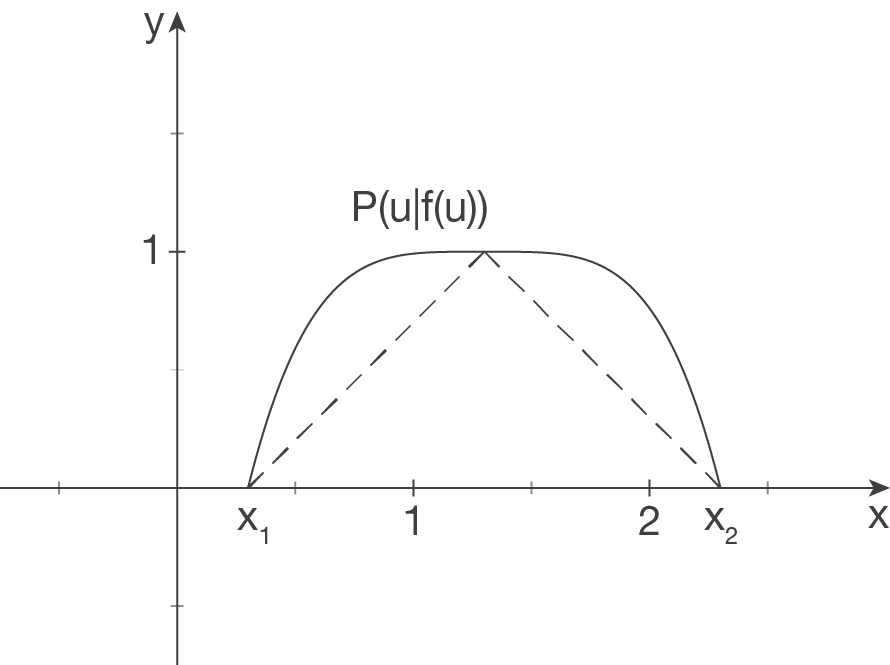Graph einer Funktion mit Achsenbezeichnungen und einer Kurve, die ein Maximum zeigt.

Die Länge der Grundkante ist bereits bekannt, sie beträgt $x_2-x_1$ LE.
Die Länge der Seitenkanten allerdings muss noch berechnet werden. Dies geschieht mit Hilfe des Satzes von Pythagoras. Die Linke Kante nennen wir $s_1$ , die rechte $s_2$ .

Skizze zu $s_1$ :

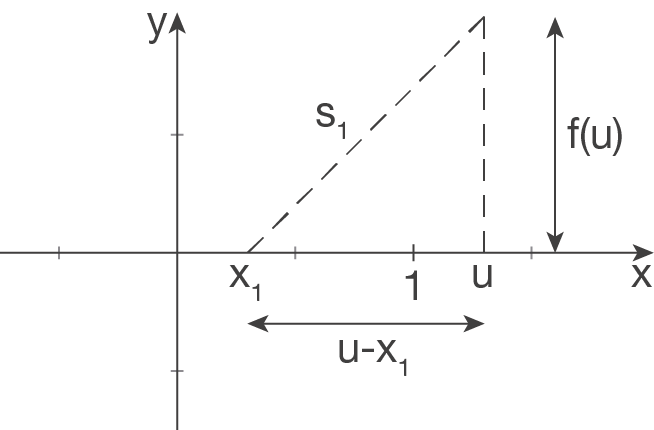
Diagramm mit Koordinatenachsen und einem rechtwinkligen Dreieck zur Veranschaulichung von Funktionen.

$\begin{array}[t]{rll} s_1=&\sqrt{\left(u-x_1\right)^2+\left(f\left(u\right)\right)^2}\\ \end{array}$

Skizze zu $s_2$ :

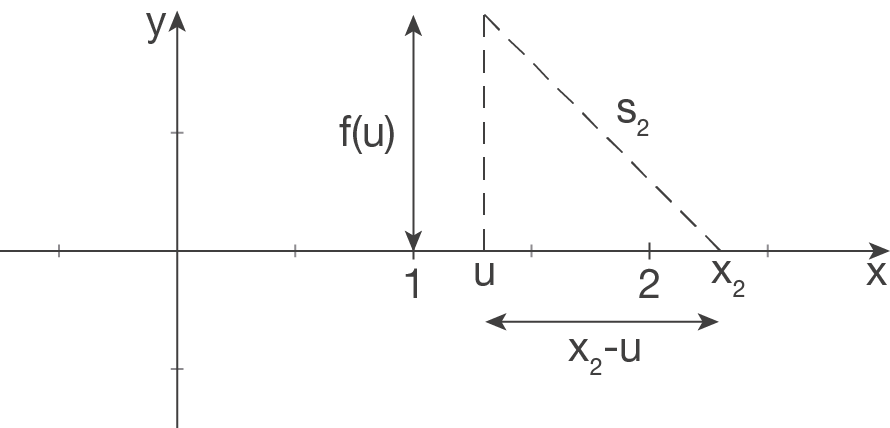
Diagramm eines Koordinatensystems mit Achsenbeschriftungen und einer Funktion f(u).

$\begin{array}[t]{rll} s_2=&\sqrt{\left(x_2-u\right)^2+\left(f\left(u\right)\right)^2} \end{array}$

$U=x_2-x_1+\sqrt{...}+\sqrt{...}$

Vollständige Lösung anzeigen

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?