Vermischte Aufgaben
1.
Berechne die Integrale.
![\(\displaystyle\int_{0}^{1} \left[\dfrac{3}{2}\cdot(3x-2)^{5}\right]\,\mathrm dx\)](https://mathjax.schullv.de/fdc80c74d0580aa487fdb126684b1da40b3c07521a631fdf939cb696805b2230?color=5a5a5a)
![\(\displaystyle\int_{1}^{2} \left[2\cdot\left(5x-8\right)^{3}\right]\,\mathrm dx\)](https://mathjax.schullv.de/27ec9d0a42dcb886691ba908250584c70f7091851ee3d60db7722cd893bb5e41?color=5a5a5a)
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
2.
Die Parabel mit der Gleichung 
schließt gemeinsam mit der 
-Achse eine Fläche vollständig ein.
Berechne den Inhalt dieser Fläche.
3.
Der Graph der Funktion 
mit 
, die -Achse und die beiden Geraden 
und 
schließen eine Fläche vollständig ein.
Zeichne den Graphen dieser Funktion in ein Koordinatensystem und berechne den Inhalt der
eingeschlossenen Fläche.
eingeschlossenen Fläche.
4.
Finde für die Funktion eine mögliche Stammfunktion 
.
a)
b)
c)
d)
5.
Die Parabel mit der Gleichung 
schließt zusammen mit der -Achse und der Geraden 
eine Fläche ein. Diese Fläche ist in zwei Teilflächen unterteilt.
Berechne den Inhalt der Gesamtfläche.
6.
Die Parabel mit der Gleichung 
und die Gerade 
, die parallel zur Tangente an an der Stelle 
ist und durch den Ursprung geht, schließen eine Fläche vollständig ein.
Bestimme deren Flächeninhalt.
7.
Begründe, warum die Funktion mit 
die Asymptote 
besitzt.
Berechne den Inhalt der Fläche, die vom Graphen von , dieser Asymptote und den Geraden 
und
eingeschlossen wird.
8.
Der Graph der Funktion mit 
schließt zusammen mit der Geraden 
und der 
-Achse eine Fläche ein, die nach links ins Unendliche reicht.
Zeichne den Graphen von und die Gerade in ein gemeinsames Koordinatensystem und zeige, dass der
Inhalt der Fläche einen endlichen Wert annimmt.
Inhalt der Fläche einen endlichen Wert annimmt.
9.
Bestimme diejenige Stammfunktion von mit 
, deren
Schaubild den Tiefpunkt auf der -Achse hat.
10.
Bestimme zu mit
die Integralfunktion 
mit 
.
11.
Bestimme zu mit 
die Integralfunktion mit 
.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
Vollständige Lösung anzeigen
b)
c)
d)
e)
f)
g)
h)
i)
j)
2.
1. Schritt: Grenzen des Integrals berechnen:
Die Fläche wird vom Graphen von
und der -Achse vollständig eingeschlossen. Die Grenzen des Integrals sind also die Nullstellen der Funktion .
2. Schritt: Flächeninhalt berechnen:
3.
1. Schritt: Besondere Punkte des Graphen berechnen:
Teil der Aufgabe ist es, den Graphen von
zu zeichnen. Untersuche also zunächst die Funktion auf Nullstellen und Extremstellen.
Nullstellen bestimmen:
Extremstellen bestimmen:
Die ersten zwei Ableitungen der Funktion
haben die Gleichungen
und 
. Aus dem notwendigen Kriterium für
Extremstellen folgt:
Mit 
ist das
hinreichende Kriterium für ein Maximum erfüllt. Berechne die zugehörige
-Koordinate:
.
Der Graph von besitzt den Hochpunkt 
.
Graph skizzieren:
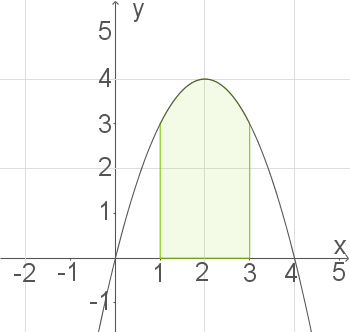2. Schritt: Flächeninhalt berechnen:
4.
a)
b)
c)
d)
5.
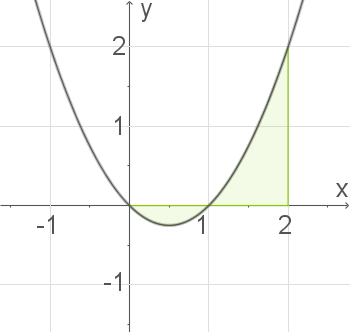
1. Schritt: Grenzen des Integrals berechnen:
Die Fläche wird vom Graphen von
und der -Achse vollständig eingeschlossen. Die Grenzen des Integrals sind also die Nullstellen der Funktion .
![\(\begin{array}{llllllll}
x^2-x&=0\\[3pt]
x(x-1)&=0\\[3pt]
x_1&=0\\[3pt]
x_2&=1
\end{array}\)](https://mathjax.schullv.de/7893c9722006981d494ee9d13d62778734f46e7c4667f1c605a007db55764502?color=5a5a5a)
2. Schritt: Flächeninhalt berechnen:
Die Gesamtfläche beträgt somit:
FE
6.
1. Schritt: Funktionsgleichung der Parabel bestimmen:
Die Gerade verläuft parallel zur Tangenten, die den Graphen von an der Stelle berührt.
Parallele Geraden besitzen die gleiche Steigung. Bestimme also die Steigung der Tangenten mit der ersten Ableitung:![\(\begin{array}{rlll}
f(x)&=-x^2+8\\[3pt]
f‘(x)&=-2x\\[3pt]
f‘(-1)&=2=m
\end{array}\)](https://mathjax.schullv.de/43ecbb7267f78c3be392938bb593d3a0e099805c15248d75e5470d528f71aa9b?color=5a5a5a)
Die Gerade verläuft durch den
Ursprung und hat damit die Funktionsgleichung 
.
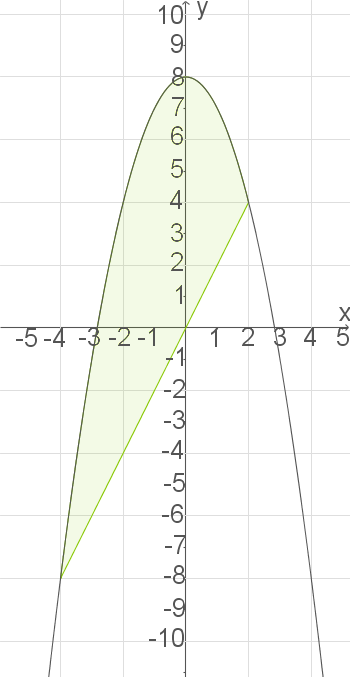2. Schritt: Flächeninhalt berechnen:
Die Fläche wird vom Graphen von und
der Geraden vollständig eingeschlossen. Berechne deren Schnittstellen durch Gleichsetzen.
Für den Inhalt der Fläche gilt dann:
Parallele Geraden besitzen die gleiche Steigung. Bestimme also die Steigung der Tangenten mit der ersten Ableitung:
7.
1. Schritt: Gleichung der Asymptote begründen:
Das Schaubild der Funktion mit hat die Gerade
als Asymptote, da für 
gilt:
Daher gilt: 
.
Die Gerade ist somit Asymptote.
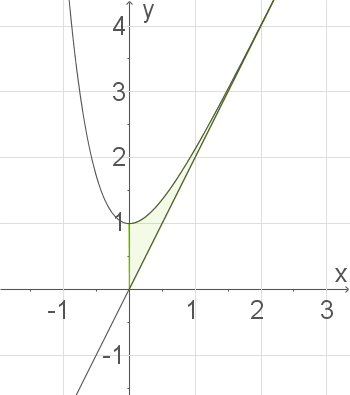2. Schritt: Flächeninhalt berechnen:
Die Fläche wird vom Graphen von , der Asymptoten und den Geraden und eingeschlossen. Berechne deren Schnittstellen durch Gleichsetzen.
8.
1. Schritt: Graph zeichnen:
Der Graph von mit 
entsteht aus dem Graphen der 
-Funktion durch Spiegelung an der -Achse und anschließende Verschiebung um 
LE nach oben.
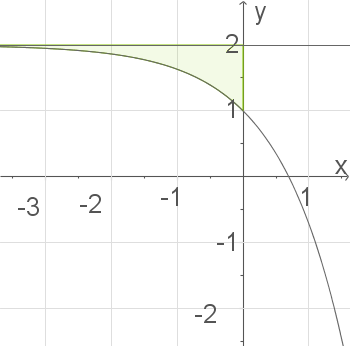2. Schritt: Flächeninhalt berechnen:
Die Fläche wird eingeschlossen vom Graphen von , der Geraden und der -Achse. Die untere Grenze des Integrals ist 
mit 
.
![\(\begin{array}{rlll}
A(a)&=\left|\displaystyle\int_{a}^{0}(2-f(x))\,\mathrm dx\right|\\[6pt]
&=\left|\displaystyle\int_{a}^{0}(2-(2-\mathrm{e}^{x}))\,\mathrm dx\right|\\[6pt]
&=\left|\displaystyle\int_{a}^{0}\mathrm{e}^{x}\,\mathrm dx\right|\\[6pt]
&=\left[\mathrm{e}^{x}\right]_a^0=1-\mathrm{e}^{a}
\end{array}\)](https://mathjax.schullv.de/c792a3350ec2c4688885273fd57930780c711c0da32fc9fad465b3c1a36c0aa4?color=5a5a5a)
Die Fläche reicht nach links ins Unendliche. Betrachte also 
mit 
:
Der Inhalt der Fläche nimmt einen endlichen Wert an.
9.
Stammfunktion bestimmen
Als allgemeine Gleichung
der Stammfunktion von erhältst du: 
.
Der Graph von soll einen Tiefpunkt auf der -Achse besitzen. Berechne also die Extremstellen von . Diese sind
die Nullstellen von (da 
).
![\(\begin{array}{rlll}
f(x)&=x^3-4x=0\\[3pt]
x(x^2-4)&=0\\[3pt]
x_1&=0\\[3pt]
x_{2,3}&=\pm2
\end{array}\)](https://mathjax.schullv.de/48f8198f2cc710490e5dafb8e10f949296a4f5b69faa0c63661b939d9c73c7aa?color=5a5a5a)
Das Einsetzen der Extremstellen in
liefert:
(0|0)
(-2|-4+c)
(2|-4+c)
Der bzw. die Tiefpunkte liegen auf der
-Achse, wenn gilt:
Die gesuchte Stammfunktion ist:
10.
Für die Integralfunktion ergibt sich:
11.
Für die Integralfunktion ergibt sich: