Mehrstufige Zufallsexperimente
Ein mehrstufiges Zufallsexperiment ist sozusagen die Hintereinanderschaltung mehrerer einstufiger Zufallsexperimente. Die Ergebnismenge eines mehrstufigen Zufallsexperiment mit 
Stufen ergibt sich wie folgt, dabei sind 
, ..., 
die Ergebnismengen der jeweiligen Stufe:
Beispiele
Folgende sind mehrstufige Zufallsexperimente:- Mehrmaliges Werfen einer Münze und notieren der einzelnen Ergebnisse
- Mehrmaliges Drehen eines Glücksrads und notieren der einzelnen Ergebnisse
- Mehrmaliges Werfen eines Würfels und notieren der einzelnen Ergebnisse
Vollständige Lösung anzeigen
1.
Es wird zweimal gewürfelt. Gib die Ergebnismenge an.
Könnte man das Zufallsexperiment auch durch eine Urnenziehung mit bzw. ohne Zurücklegen darstellen?
Könnte man das Zufallsexperiment auch durch eine Urnenziehung mit bzw. ohne Zurücklegen darstellen?
2.
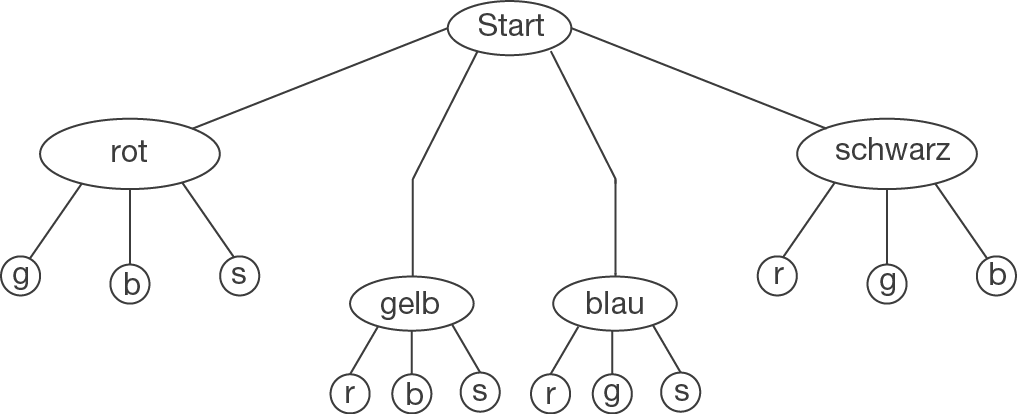
Aus einer Urne mit vier Kugeln (rot, gelb, blau, schwarz) wird zweimal ohne Zurücklegen gezogen.
Gib die Ergebnismenge an und zeichne ein passendes Baumdiagramm.
Gib die Ergebnismenge an und zeichne ein passendes Baumdiagramm.
3.
In einem McDonald‘s Restaurant steht ein Glücksrad mit sechs Gewinnfeldern. Dreht man das Rad, so zeigt ein Zeiger auf genau einen Gutschein (Big Mac, kleines Getränk, Happy Meal, Cheeseburger, kleine Pommes, Kaffee).
Peter darf zweimal drehen. Gib die Ergebnismenge an.
Peter darf zweimal drehen. Gib die Ergebnismenge an.
4.
Martin überführt auf dem Weg zur Arbeit jeden Morgen zwei Ampeln, die unabhängig voneinander geschaltet sind.
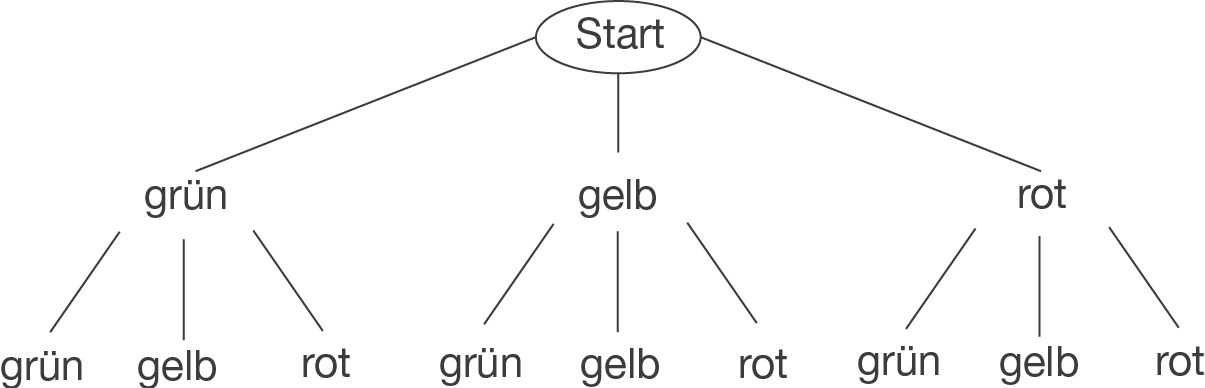
Gib die Ergebnismenge für die verschiedenen Ampelfarben an und zeichne ein passendes Baumdiagramm.
Gib die Ergebnismenge für die verschiedenen Ampelfarben an und zeichne ein passendes Baumdiagramm.
5.
Aus einer Urne mit vier roten und vier schwarzen Kugeln werden zwei Kugeln ohne Hinsehen gezogen.
Führe den Zufallsversuch auf zwei verschiedene Arten durch und gib die Ergebnismenge
an:
Führe den Zufallsversuch auf zwei verschiedene Arten durch und gib die Ergebnismenge
a)
Es kommt auf die Reihenfolge an.
b)
Es kommt nicht auf die Reihenfolge an.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
Ergebnismenge angeben
Darstellung im Urnenmodell
In einer Urne befinden sich
Kugeln, die mit 
bis beschriftet sind. Es wird zwei Mal mit Zurücklegen gezogen.
Darstellung im Urnenmodell
In einer Urne befinden sich
2.
Ergebnismenge angeben und Baumdiagramm zeichnen
(rot 
r, gelb g, blau b, schwarz s)
Ein mögliches Baumdiagramm ist:
3.
Ergebnismenge angeben
(Big Mac B, Getränk G, Happy Meal H, Cheeseburger C, kleine Pommes P, Kaffee K)
Ohne Berücksichtigung der Reihenfolge ergibt sich die Ergebnismenge
4.
Ergebnismenge angeben und Baumdiagramm zeichnen
(grün gr, gelb ge, rot r)
Die Ergebnismenge ist:
5.
Ergebnismenge angeben
a)
Im ersten Fall gibt es die Ergebnisse:
Die Ergebnismenge ist also 
| „beide Kugeln rot“ | (rr) |
| „erste Kugel rot, zweite schwarz“ | (sr) |
| „erste Kugel schwarz, zweite rot“ | (rs) |
| „beide Kugeln schwarz“ | (ss) |
b)
Im zweiten Fall kann man nur nach der Farbe unterscheiden, die Ergebnismenge besteht daher nur aus drei Elementen:
