Vermischte Aufgaben

Gegeben sind die zwei Geraden

$g:\; \overrightarrow x = \left( \begin{array}{r} 1 \\ 0 \\ 1 \\ \end{array} \right) + s\left( \begin{array}{c} 2 \\ a \\ a^2 \\ \end{array} \right)$ und $h:\;\overrightarrow x = \left( \begin{array}{c} 2\\ 3 \\ a^2-a+1 \\ \end{array} \right) + t\left( \begin{array}{c} 2 \\ a^2 \\ a \\ \end{array} \right)$ .

Untersuchen Sie für welche $a\in\mathbb{R}$ die beiden Geraden parallel sind. Sind die Geraden echt parallel oder identisch?

Geben Sie eine Gleichung für eine Gerade an, die

identisch mit $g$ ist

$g$ schneidet

parallel zu $g$ ist

windschief zu $g$ ist

$g:\;\overrightarrow{x}=\left( {\begin{array}{*{20}r} 1 \\ 0 \\ 1 \\ \end{array}} \right)+t\left( {\begin{array}{*{20}r} 3 \\ 2 \\ 0 \\ \end{array}} \right)$

$g:\;\overrightarrow{x}=\left( {\begin{array}{*{20}r} 1 \\ 1 \\ 2 \\ \end{array}} \right)+t\left( {\begin{array}{*{20}r} 3 \\ 4 \\ -1 \\ \end{array}} \right)$

Gibt es ein $t$ , sodass sich $g$ und $h$ schneiden (parallel, identisch oder windschief sind)? Wenn ja welches?

$g:\;\overrightarrow{x}=\left( {\begin{array}{*{20}r} 1 \\ 2 \\ t \\ \end{array}} \right)+s\left( {\begin{array}{*{20}r} -1 \\ 4 \\ 5 \\ \end{array}} \right)$ , $\qquad$ $h:\;\overrightarrow{x}=\left( {\begin{array}{*{20}r} 3t \\ 2 \\ -1 \\ \end{array}} \right)+r\left( {\begin{array}{*{20}r} -1 \\ -2 \\ -4 \\ \end{array}} \right)$ .

$g:\;\overrightarrow{x}=s\left( {\begin{array}{*{20}r} -32 \\ t \\ -2 \\ \end{array}} \right)$ , $\qquad$ $h:\;\overrightarrow{x}=r\left( {\begin{array}{*{20}r} -2t \\ 4 \\ 1 \\ \end{array}} \right)$ .

Gegeben ist eine Gerade $g:\;\overrightarrow{x}=\overrightarrow{p}+s\cdot\overrightarrow{u} \quad s\in\mathbb{R}$ .

Geben Sie einen Richtungsvektor $\overrightarrow{u}$ an, sodass die Gerade $g$

parallel zur $x_2$ -Achse ist.

parallel zur $x_1x_2$ -Ebene ist.

orthogonal zur Ebene $H:\; 2x_1+4x_2=3$ ist.

parallel zur Ebene $H:\; 2x_1+4x_2=3$ ist.

Gegeben sind die Punkte $A(0 \mid 2 \mid 1)$ , $B(-5 \mid 7 \mid 11)$ , $C(0 \mid 0 \mid 0)$ und $D(4 \mid -4 \mid 7)$ .

Die Gerade $g$ geht durch die Punkte $A$ und $B$ . Die Gerade $h$ durch die Punkte $C$ und $D$ .

Stellen Sie eine Geradengleichung von $g$ und $h$ auf. Wie liegen die beiden Geraden zueinander?

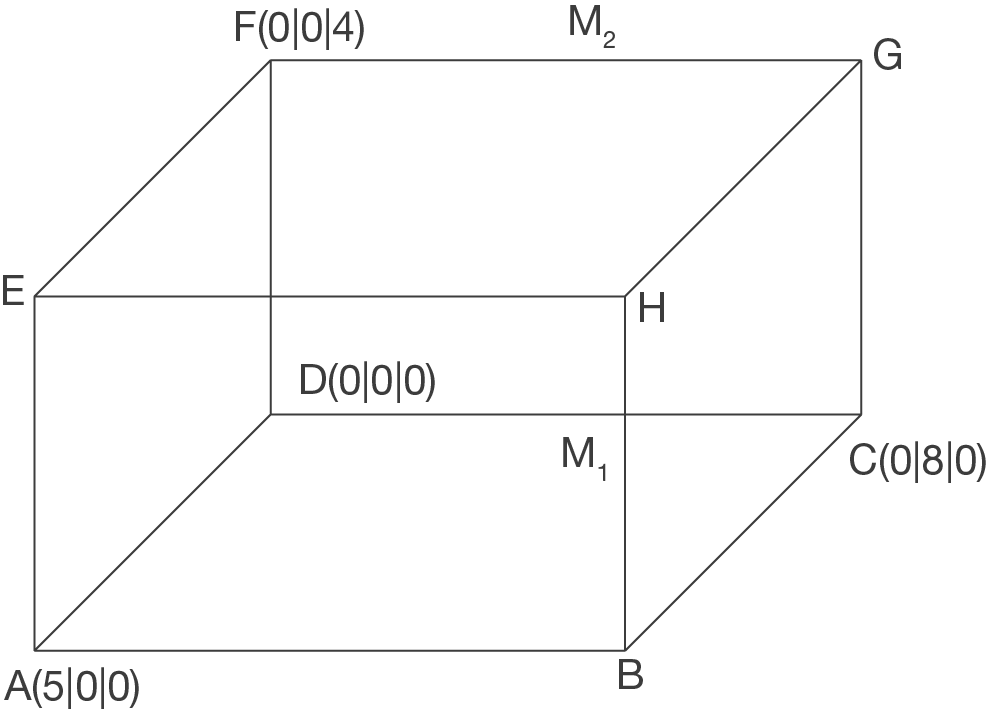
Ein Quader ist wie in der Figur unten gegeben. $M_1$ und $M_2$ sind Mittelpunkte der zugehörigen Kanten

3D-Diagramm eines Quaders mit beschrifteten Punkten und Koordinaten.

Welche Lage haben die Geraden $g$ durch $AG$ und $h$ durch $M_1M_2$ zueinander? Begründe rechnerisch.

Geben Sie eine Koordinatengleichung der Ebene an, die $D$ , $E$ und $G$ enthält.

Gegeben sind Ebenen $E$ , $F$ , $G$ und $H$ mit

$E:\;-3x+2y-7z=2$

$F:\;9x-6y+21z=0$

$G:\;\dfrac{1}{2}x-4y=1$

$H:\;x+2y-z=5$

Wie liegen $E$ und $F$ zueinander? Begründe ohne weitere Rechnung.

Was müsste man auf der rechten Seite der Koordinatengleichung ändern, damit $E$ und $F$ identisch sind?

Welche besondere Lage hat die Ebene $G$ im Koordinatensystem? Begründe.

Bestimmen Sie die Schnittgerade von $E$ und $H$ .

Die Ebene $E$ geht durch die Punkte $A(1,5\, \mid \,0\, \mid \,0)$ , $B(0\, \mid \,3\, \mid \,0)$ und $C(0\, \mid \,0\, \mid \,6)$ .

Untersuchen Sie, ob die Gerade $g$ : $\vec{x}=\begin{pmatrix} -4 \\ 2 \\ 3 \end{pmatrix}+t\begin{pmatrix} -2 \\ 3 \\ 2 \end{pmatrix};$ $t \in \mathbb{R}$ parallel zur Ebene $E$ verläuft.

$\scriptsize{\text{ Aus dem Pflichtteil 2008}}$

Gegeben sind die beiden Ebenen $E_1$ : $(\vec{x}-\vec{p}_1) \cdot \vec{n}_1=0$ und $E_2$ : $(\vec{x}-\vec{p}_2) \cdot \vec{n}_2=0$ .

Beschreiben Sie ein Verfahren, mit dem man anhand dieser Normalengleichungen die gegenseitige Lage der beiden Ebenen untersuchen kann.

$\scriptsize{\text{ Aus dem Pflichtteil 2008}}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Damit die Geraden $g$ und $h$ parallel sind, müssen ihre Richtungsvektoren linear abhängig sein.

$\left( {\begin{array}{*{20}c} 2 \\ a \\ a^2 \\ \end{array}} \right)$ = $k \cdot \left( {\begin{array}{*{20}c} 2 \\ a^2 \\ a \\ \end{array}} \right)$

$\begin{array}{rrll} &2=&2k&\quad \Rightarrow\; k=1\\[5pt] \quad\Rightarrow\;&a=&ka^2& \\[5pt] &a^2=&ka& \\[5pt] \end{array}$

Mit $k=1$ muss für die zweite und dritte Gleichung $a=a^2 \Leftrightarrow a^2=a$ gelten.

Diese Gleichung ist für $a=0$ und $a=1$ erfüllt.

Für diese Werte von $a$ sind die Richtungsvektoren somit linear abhängig.

Um zu überprüfen, ob die Geraden identisch sind, setzt man die Werte in die Geradengleichungen ein und überprüft, ob der Stützvektor von $g$ (also der Punkt $(1 \mid 0 \mid 1)$ ) auf $h$ liegt.

$a=0$ : $\qquad$ $h:\;\overrightarrow x$ = $\left( \begin{array}{r} 2\\ 3 \\ 1 \\ \end{array} \right) + t\left( \begin{array}{r} 2 \\ 0 \\ 0\\ \end{array} \right)$

Punkt $(1 \mid 0 \mid 1)$ einsetzen:

$\left( \begin{array}{r} 1\\ 0 \\ 1 \\ \end{array} \right)=\left( \begin{array}{r} 2\\ 3 \\ 1 \\ \end{array} \right) + t\left( \begin{array}{r} 2 \\ 0 \\ 0\\ \end{array} \right)$

$\begin{array}{rll} &1=&1& \\[5pt] \end{array}$

Vollständige Lösung anzeigen

Der Punkt liegt für $a=0$ nicht auf der Geraden $h$ .

$a=1$ : $\qquad$ $h:\;\overrightarrow x$ = $\left( \begin{array}{r} 2\\ 3 \\ 1 \\ \end{array} \right) + t\left( \begin{array}{r} 2 \\ 1 \\ 1\\ \end{array} \right)$

Punkt $(1 \mid 0 \mid 1)$ einsetzen:

$\left( \begin{array}{r} 1\\ 0 \\ 1 \\ \end{array} \right)$ = $\left( \begin{array}{r} 2\\ 3 \\ 1 \\ \end{array} \right) + t\left( \begin{array}{r} 2 \\ 1 \\ 1\\ \end{array} \right)$

$\begin{array}{rll} &1=&2+t&\quad\Rightarrow\;t=-1\\[5pt] \quad\Rightarrow\;&0=&3+t&\quad\Rightarrow\;t=-3 \\[5pt] &1=&1+t& \quad\Rightarrow\;t=0\\[5pt] \end{array}$

Der Punkt liegt für $a=1$ nicht auf der Geraden $h$ .

Somit sind die Geraden für $a=0$ und $a=1$ echt parallel.

$g:\;\overrightarrow{x}$ = $\left( {\begin{array}{*{20}r} 1 \\ 0 \\ 1 \\ \end{array}} \right)+t\left( {\begin{array}{*{20}r} 3 \\ 2 \\ 0 \\ \end{array}} \right)$

$\blacktriangleright$ Identisch mit $g$

Sind Geraden identisch, so haben sie unendlich viele Punkte gemeinsam und ihre Richtungsvektoren sind linear abhängig.

$t=2$ eingesetzt in $g$ liefert den Ortsvektor eines weiteren Punktes auf der Geraden:

$\left( {\begin{array}{*{20}r} 1 \\ 0 \\ 1 \\ \end{array}} \right)+2\left( {\begin{array}{*{20}r} 3 \\ 2 \\ 0 \\ \end{array}} \right)$ = $\left( {\begin{array}{*{20}r} 7 \\ 4 \\ 1 \\ \end{array}} \right)$

Identische Gerade: z.B. $g‘:\;\overrightarrow x$ = $\left( {\begin{array}{*{20}r} 7 \\ 4 \\ 1 \\ \end{array}} \right)+s\left( {\begin{array}{*{20}r} 6 \\ 4 \\ 0 \\ \end{array}} \right)$

$\blacktriangleright$ Gerade, die g schneidet

Damit sich die Geraden schneiden, müssen die Geraden linear unabhängige Richtungsvektoren haben und einen Punkt gemeinsam.

Linear unabhängig Vektor zu $\left( {\begin{array}{*{20}r} 3 \\ 2 \\ 0 \\ \end{array}} \right)$ ist z.B. $\left( {\begin{array}{*{20}r} 0 \\ 0 \\ 1 \\ \end{array}} \right)$

Als gemeinsamer Schnittpunkt bietet sich der Punkt $(1 \mid 0 \mid 1)$ auf der Geraden $g$ an.

Die Gleichung einer Geraden, die $g$ schneidet lautet z.B. $g‘:\;\overrightarrow x$ = $\left( {\begin{array}{*{20}r} 1 \\ 0 \\ 1 \\ \end{array}} \right)+s\left( {\begin{array}{*{20}r} 0 \\ 0 \\ 1 \\ \end{array}} \right)$

$\blacktriangleright$ Parallel zu $g$

Parallele Geraden haben linear abhängige Richtungsvektoren, aber keine Punkte gemeinsam.

$\left( {\begin{array}{*{20}r} -3 \\ -2 \\ 0 \\ \end{array}} \right)$ und $\left( {\begin{array}{*{20}r} 3 \\ 2 \\ 0 \\ \end{array}} \right)$ sind linear abhängig.

Der Punkt $P(1 \mid 2 \mid 3)$ liegt nicht auf $g$ .

Die Gleichung einer Geraden die parallel zu $g$ ist lautet z.B. $g‘:\;\overrightarrow x=\left( {\begin{array}{*{20}r} 1 \\ 2 \\ 3 \\ \end{array}} \right)+s\left( {\begin{array}{*{20}r} -3 \\ -2 \\ 0 \\ \end{array}} \right)$

$\blacktriangleright$ Windschief zu $g$

Windschiefe Geraden haben linear unabhängige Richtungsvektoren und keinen Punkt gemeinsam.

Der Punkt $P(1 \mid 2 \mid 3)$ liegt nicht auf $g$ und der Vektor $\left( {\begin{array}{*{20}r} 0 \\ 0 \\ 1 \\ \end{array}} \right)$ ist linear unabhängig zu dem Richtungsvektor von $g$ .

Eine mögliche Gleichung der zu $g$ windschiefen Geraden $g‘$ lautet somit

$g‘:\;\overrightarrow x$ = $\left( {\begin{array}{*{20}r} 1 \\ 2 \\ 3 \\ \end{array}} \right)+s\left( {\begin{array}{*{20}r} 0 \\ 0 \\ 1 \\ \end{array}} \right)$

$g:\;\overrightarrow{x}$ = $\left( {\begin{array}{*{20}r} 1 \\ 1 \\ 2 \\ \end{array}} \right)+t\left( {\begin{array}{*{20}r} 3 \\ 4 \\ -1 \\ \end{array}} \right)$

$\blacktriangleright$ Identisch mit $g$

z.B. $g‘:\;\overrightarrow x$ = $\left( {\begin{array}{*{20}r} 1 \\ 1 \\ 2 \\ \end{array}} \right)+s\left( {\begin{array}{*{20}r} 6 \\ 8 \\ -2 \\ \end{array}} \right)$

$\blacktriangleright$ Gerade, die g schneidet

Ein linear unabhängig Vektor zu $\left( {\begin{array}{*{20}r} 3 \\ 4 \\ -1 \\ \end{array}} \right)$ ist z.B. $\left( {\begin{array}{*{20}r} -1 \\ 0 \\ -1 \\ \end{array}} \right)$

Die Gleichung einer Geraden, die $g$ schneidet lautet z.B. $g‘:\;\overrightarrow x=\left( {\begin{array}{*{20}r} 1 \\ 1 \\ 2 \\ \end{array}} \right)+s\left( {\begin{array}{*{20}r} -1 \\ 0 \\ -1 \\ \end{array}} \right)$

$\blacktriangleright$ Parallel zu $g$

Der Punkt $P(1 \mid 0 \mid 0)$ liegt nicht auf $g$ .

Die Gleichung einer Geraden die parallel zu $g$ ist lautet z.B. $g‘:\;\overrightarrow x=\left( {\begin{array}{*{20}r} 1 \\ 0 \\ 0 \\ \end{array}} \right)+s\left( {\begin{array}{*{20}r} -3 \\ -4 \\ 1 \\ \end{array}} \right)$

$\blacktriangleright$ Windschief zu $g$

Der Punkt $P(1 \mid 0 \mid 0)$ liegt nicht auf $g$ und der Vektor $\left( {\begin{array}{*{20}r} -1 \\ 0 \\ -1 \\ \end{array}} \right)$ ist linear unabhängig zu dem Richtungsvektor von $g$ .

Eine mögliche Gleichung der zu $g$ windschiefen Geraden $g‘$ lautet somit

$g‘:\;\overrightarrow x$ = $\left( {\begin{array}{*{20}r} 1 \\ 0 \\ 0 \\ \end{array}} \right)+s\left( {\begin{array}{*{20}r} -1 \\ 0 \\ -1 \\ \end{array}} \right)$

$\blacktriangleright$ Überprüfen, ob $g$ und $h$ sich schneiden

Da die Richtungsvektoren linear unabhängig sind, muss man nur noch überprüfen, ob die Geraden sich für ein $t\in\mathbb{R}$ schneiden:

$\left( {\begin{array}{*{20}r} 1 \\ 2 \\ t \\ \end{array}} \right)+s\left( {\begin{array}{*{20}r} -1 \\ 4 \\ 5 \\ \end{array}} \right)$ = $\left( {\begin{array}{*{20}r} 3t \\ 2 \\ -1 \\ \end{array}} \right)+r\left( {\begin{array}{*{20}r} -1 \\ -2 \\ -4 \\ \end{array}} \right)$

Erhalte LGS:

$\begin{array}{lrll} Ⅰ& 1-s=&3t-r& \\[5pt] Ⅱ& 2+4s=&2-2r& \\[5pt] Ⅲ& t+5s=&-1-4r&\\[5pt] \end{array}$

Vollständige Lösung anzeigen

$-2s=r$ eingesetzt in Ⅰ:

$1-s=3t+2s \quad \Rightarrow \quad \dfrac{1}{3}-s=t$

Setze nun $r=-2s$ und $t=\frac{1}{3}-s$ ein in Gleichung Ⅲ:

$\begin{array}{rlll} \dfrac{1}{3}=&s \end{array}$

Vollständige Lösung anzeigen

Setzt zuletzt $s=\frac{1}{3}$ ein in $t=\frac{1}{3}-s$ und erhalte so den Wert für $t$ , für den ein Schnittpunkt existiert:

$t=\dfrac{1}{3}-\dfrac{1}{3}=0$

Für $t=0$ schneiden sich die Geraden.

$\blacktriangleright$ Zur Parallelität bzw. zur Identität

Die Geraden können nur identisch sein, wenn sie mindestens parallel sind. Wenn sie nicht parallel sind, dann kann die Identität gleich ausgeschlossen werden. Parallel verlaufen zwei Geraden, wenn ihre Richtungsvektoren linear abhängig, also Vielfache voneinander sind. Du erkennst, dass dies bei diesen beiden Geraden nicht der Fall ist:

Während die erste Koordinate der Richtungsvektoren übereinstimmt, liegt bei der zweiten Koordinate bereits eine Abweichung vor, auch die dritte Koordinate passt nicht ins Bild. Also können die Geraden für keine Wahl von $t$ parallel oder identisch sein.

Da nur für $t=0$ ein Schnittpunkt vorliegt und die Geraden weder windschief noch identisch sein können, folgt automatisch: Für alle Werte von $t$ mit $t\neq0$ sind die Geraden windschief. Parallel und identisch können die Geraden auch nicht sein, da die Richtungsvektoren linear unabhängig sind.

Schaut man sich die Richtungsvektoren an so sind diese linear abhängig, wenn gilt:

$\left( {\begin{array}{*{20}r} -32 \\ t \\ -2 \\ \end{array}} \right)$ = $k\cdot\left( {\begin{array}{*{20}r} -2t \\ 4 \\ 1 \\ \end{array}} \right)$

$\begin{array}{rrll} &-32=&-2tk&\\[5pt] \quad\Rightarrow\;&t=&4k&\\[5pt] &-2=&k& \\[5pt] \end{array}$

Setzt du $k=-2$ in die zweite Zeile ein erhältst du: $t=4\cdot\left(-2\right)=-8$

Mit $k=-2$ und $t=-8$ eingesetzt in die erste Gleichung ergibt sich $-32=-2\cdot\left(-8\right)\cdot\left(-2\right)$ $=-32$ . Damit sind die Richtungsvektoren von $g$ und $h$ für $t=-8$ linear abhängig. Für alle anderen $t$ sind die Richtungsvektoren linear unabhängig. Da die beiden Geraden durch den Ursprung gehen sind sie somit für $t=-8$ identisch. (Es gibt kein $t$ , so dass die Geraden parallel sind)

Für alle $t\in\mathbb{R}\setminus\left\{-8\right\}$ schneiden sich somit die zwei Geraden in einem Punkt. Da die Geraden beide durch den Ursprung gehen sind sie für kein $t$ windschief.

Für die Gerade $g:\;\overrightarrow{x}$ = $\overrightarrow{p}+s\cdot\overrightarrow{u}; \; s\in\mathbb{R}$ gilt:

Für $\overrightarrow{u}$ = $\left( {\begin{array}{*{20}r} 0 \\ { 1} \\ 0 \\ \end{array}} \right)$ ist $g$ parallel zur $x_2$ -Achse, da $\overrightarrow{u}$ auch ein Richtungsvektor der $x_2$ -Achse ist.

Für $\overrightarrow{u}=\left( {\begin{array}{*{20}r} 1\\ { 1} \\ 0 \\ \end{array}} \right)$ ist $g$ parallel zur $x_1x_2$ -Ebene.

Der Vektor $\overrightarrow{n}$ = $\left( {\begin{array}{*{20}r} 0 \\ { 0} \\ 1 \\ \end{array}} \right)$ steht senkrecht auf der $x_1x_2$ -Ebene und allen Geraden, die parallel zu dieser Ebene sind. Es gilt $\overrightarrow{u}\cdot\overrightarrow{n}=0$ .

Für $\overrightarrow{u}=\left( {\begin{array}{*{20}r} 2\\ { 4} \\ 0 \\ \end{array}} \right)$ ist $g$ Orthogonal zur Ebene $H:\; 2x_1+4x_2=3$ , da $\overrightarrow{u}$ ein Normalenvektor von $H$ ist.

Für $\overrightarrow{u}=\left( {\begin{array}{*{20}r} -4\\ { 2} \\ 0 \\ \end{array}} \right)$ ist $g$ parallel zur Ebene $H:\; 2x_1+4x_2=3$ ,

da der Vektor $\overrightarrow{n}$ = $\left( {\begin{array}{*{20}r} 2\\ { 4} \\ 0 \\ \end{array}} \right)$ ein Normalenvektor von $H$ ist und senkrecht auf $\overrightarrow{u}$ steht:

$\overrightarrow{u}\cdot\overrightarrow{n}$ = $-4\cdot2+2\cdot4+0\cdot0=0$ .

Bestimmung der Gerade $g$ durch $A(0 \mid 2 \mid 1)$ und $B(-5 \mid 7 \mid 11)$ :

$g:\overrightarrow {x}$ = $\left( \begin{array}{r} 0 \\ 2 \\ 1 \\ \end{array} \right) + s\left( \begin{array}{r} -5 \\ 5 \\ 10 \\ \end{array} \right)$

Vollständige Lösung anzeigen

Bestimmung der Geraden $h$ durch $C(0 \mid 0 \mid 0)$ und $D(4 \mid -4 \mid 7)$ :

$h:\overrightarrow {x}$ = $t\left( \begin{array}{r} 4 \\ -4 \\ 7 \\ \end{array} \right)$

Bestimmung der Lage der beiden Geraden:

$\left( \begin{array}{r} 0 \\ 2 \\ 1 \\ \end{array} \right) + s\left( \begin{array}{r} -5 \\ 5 \\ 10 \\ \end{array} \right)$ = $t\left( \begin{array}{r} 4\\ -4 \\ 7 \\ \end{array} \right)$

$\begin{array}{rrll} &0-5s=&4t&\\[5pt] \quad\Rightarrow\;&2+5s=&-4t&\quad\\[5pt] &1+10s=&7t&\quad\\[5pt] \end{array}$

Vollständige Lösung anzeigen

Setzt man $s=-\dfrac{4}{5}t$ in die zweite Gleichung ein, so erhält man:

$2+5\cdot\left(-\frac{4}{5}t\right)=-4t \;\Rightarrow\; 2=0$ (Widerspruch)

Das LGS ist somit nicht lösbar, was bedeutet, dass die Geraden sich nicht schneiden.

Somit können die Geraden nur noch parallel oder windschief zueinander liegen. Schaut man sich die Richtungsvektoren an, so sieht man dass diese linear unabhängig sind, da das Gleichungssystem

$\left( \begin{array}{r} -5 \\ 5 \\ 10 \\ \end{array} \right)$ = $t\left( \begin{array}{r} 4 \\ -4 \\ 7 \\ \end{array} \right)$

$\begin{array}{rrll} &-5=&4t&\quad\Rightarrow\; t=-\frac{5}{4}\\[5pt] \quad\Rightarrow\;&5=&-4t&\quad\Rightarrow\; t=-\frac{5}{4}\\[5pt] &10=&7t&\quad\Rightarrow\; t=\frac{10}{7}\\[5pt] \end{array}$

für alle $t\in\mathbb{R}$ nicht lösbar ist. Somit liegen die Geraden windschief zueinander.

Aus der Zeichnung liest man die Punkte $M_1(5 \mid 8 \mid 2)$ , $M_2(0 \mid 4 \mid 4)$ und $G(0 \mid 8 \mid 4)$ .

Aufstellen einer Geradengleichung durch $M_1$ und $M_2$ :

$h:$ $\overrightarrow{x}$ = $\left(\begin{array}{r} 0\\ 4\\ 4\\ \end{array}\right)+t\cdot\left(\begin{array}{r} 5-0\\ 8-4\\ 2-4\\ \end{array}\right)$ = $\left(\begin{array}{r} 0\\ 4\\ 4\\ \end{array}\right)+t\left(\begin{array}{r} 5\\ 4\\ -2\\ \end{array}\right)$

Eine Gerade durch $G$ und $A(5 \mid 0 \mid 0)$ ist

$g:$ $\overrightarrow{x}$ = $\left(\begin{array}{r} 5\\ 0\\ 0\\ \end{array}\right)+s\cdot\left(\begin{array}{r} 5-0\\ 0-8\\ 0-4\\ \end{array}\right)$ = $\left(\begin{array}{r} 5\\ 0\\ 0\\ \end{array}\right)+s\left(\begin{array}{r} 5\\ -8\\ -4\\ \end{array}\right)$

Schaut man sich die Richtungsvektoren der Geraden an, so gilt

$\left(\begin{array}{r} 5\\ 4\\ -2\\ \end{array}\right)\neq s\cdot\left(\begin{array}{r} 5\\ -8\\ -4\\ \end{array}\right)$ für alle $s\in\mathbb{R}$ .

Damit sind die Richtungsvektoren linear unabhängig. Die Geraden können sich also nur noch schneiden oder windschiefen zueinander liegen.

Gleichsetzen der beiden Geraden:

$\begin{array}{rrll} g\cap h: &\pmatrix{ -5\\ 4\\ 4}=&s\cdot\pmatrix{ 5\\ -8\\ -4}-t\cdot\pmatrix{ 5\\ 4 -2} \\ \end{array}$

Vollständige Lösung anzeigen

Damit erhalten wir das LGS:

$\begin{array}{lrll} Ⅰ& -5=&5s-5t&\quad\\[5pt] Ⅱ& 4=&-8s-4t&\quad\\[5pt] Ⅲ& 4=&-4s+2t&\\[5pt]\hline Ⅰ& -5=&5s-5t&\quad\\[5pt] Ⅱ& 4=&-8s-4t&\quad\\[5pt] Ⅲa& 12=&-16s&\\[5pt] \end{array}$

Vollständige Lösung anzeigen

$s=-\dfrac{3}{4}$ eingesetzt in die zweite Gleichung liefert $t=\dfrac{1}{2}$ . Setzt man $t$ und $s$ in die erste Gleichung ein, so ergibt sich

$-5$ = $5\cdot\left(-\frac{3}{4}\right)-5\cdot\frac{1}{2} \;\Leftrightarrow\;-5$ = $-6,25$ $\;\Rightarrow$ falsche Aussage.

Die Geraden liegen daher windschief zueinander.

Bestimmung einer Koordinatengleichung der Ebene durch $D(0 \mid 0 \mid 0)$ , $E(5 \mid 0 \mid 4)$ und $G(0 \mid 8 \mid 4)$

Bestimmung einer Parameterform der Ebene:

$E:\;\overrightarrow{x}$ = $s\left(\begin{array}{r} 5\\ 0\\ 4\\ \end{array}\right)+t\left(\begin{array}{r} 0\\ 8\\ 4\\ \end{array}\right)$

Ein Koordinatenvektor ergibt sich über das Kreuzprodukt:

$\left(\begin{array}{r} 5\\ 0\\ 4\\ \end{array}\right)\times\left(\begin{array}{r} 0\\ 8\\ 4\\ \end{array}\right)$ = $\left(\begin{array}{r} -32\\ -20\\ 40\\ \end{array}\right)$

Da der Normalenvektor nur von der Richtung abhängig ist und nicht von der Länge, kann der oben errechnete Vektor mit vier gekürzt werden. Daraus ergibt sich folgende Ebenengleichung:

$E:\;-8x-5y+10z=d$

Einsetzen des Punktes $D(0 \mid 0 \mid 0)$ liefert:

$E:\;-8x-5y+10z=0$

Schaut man sich die Normalenvektoren der Ebenen an, so gilt:

$\left(\begin{array}{r} -3\\ 2\\ -7\\ \end{array}\right)$ = $-\dfrac{1}{3}\cdot\left(\begin{array}{r} 9\\ -6\\ 21\\ \end{array}\right)$ $\;\Rightarrow\;$ linear abhängig

Damit können die Ebenen nur noch parallel oder identisch sein. Tatsächlich sind sie parallel.

Würde man allerdings aus der $2\,(=d_E)$ eine $0$ oder aus der $0\,(=d_F)$ eine $-6$ machen, so wären die Ebenen identisch zueinander.

Die Ebene $G$ ist parallel zur $z$ -Achse, da die $z$ -Koordinate des Normalenvektors $0$ ist.

Bestimmung der Schnittgeraden von $E$ und $H$

$\begin{array}{rrll} Ⅰ&-3x+2y-7z=&2&\quad\\[5pt] Ⅱ&x+2y-z=&5&\quad \\[5pt]\hline Ⅰ&-3x+2y-7z=&2&\quad\\[5pt] Ⅱ&8y-10z=&17&\quad\\[5pt] \end{array}$

Vollständige Lösung anzeigen

$y=\dfrac{17}{8}+\dfrac{5}{4}z$ und $z=t$ eingesetzt in Ⅰ ergibt:

$\begin{array}{rll} -\dfrac{3}{2}t+\dfrac{3}{4}=&x&\quad\\[5pt] \end{array}$

Vollständige Lösung anzeigen

Der Lösungsvektor $s$ ist somit

$\overrightarrow{s}$ = $\left(\begin{array}{r} -\frac{3}{2}t+\frac{3}{4}\\ \frac{17}{8}+\frac{5}{4}t\\ t\\ \end{array}\right)$

Somit ergibt sich als Schnittgerade $s$

$s:\;\overrightarrow{x}$ = $\left(\begin{array}{r} \frac{3}{4}\\ \frac{17}{8}\\ 0\\ \end{array}\right)+t\left(\begin{array}{r} -\frac{3}{2}\\ \frac{5}{4}\\ 1\\ \end{array}\right)$

Die Schnittpunkte der Ebene $E$ mit den Koordinatenachsen sind gegeben, damit kann man die Koordinatengleichung direkt aufstellen:

$E$ : $4x_1+2x_2+x_3=6$

Die Gerade $g$ und $E$ sind parallel, wenn sie keinen Schnittpunkt besitzen. Es wird daher versucht, ein Schnittpunkt zu berechnen:

$\begin{array}{rll} -9=&\;6 \end{array}$

Vollständige Lösung anzeigen

Diese Gleichung ist ein Widerspruch, somit existiert kein Schnittpunkt zwischen $g$ und $E$ und die Gerade $g$ ist damit parallel zur Ebene $E$ .

Ist das Produkt der beiden Normalenvektoren gleich Null (also $\vec{n}_1 \cdot \vec{n}_2 =0$ ), dann sind die beiden Ebenen orthogonal zueinander und schneiden sich in Form einer Schnittgeraden.

Sind $\vec{n}_1$ und $\vec{n}_2$ Vielfache voneinander und liegt ein Punkt, dessen Koordinaten genau dem Ortsvektor $\vec{p}_1$ entsprechen, auf der Ebene $E_2$ , so sind die beiden Ebenen identisch.

Sind $\vec{n}_1$ und $\vec{n}_2$ Vielfache voneinander und liegt ein Punkt, dessen Koordinaten genau dem Ortsvektor $\vec{p}_1$ entsprechen, nicht auf der Ebene $E_2$ , so sind die beiden Ebenen parallel zueinander.

In allen anderen Fällen schneiden sich die beiden Ebenen in einer Schnittgerade, sind dabei jedoch nicht orthogonal zueinander.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?