Uneigentliches Integral

Uneigentliche Integrale sind Integrale, bei denen mindestens eine der beiden Grenzen $\infty$ oder $-\infty$ ist, sie haben also folgende Form:

$\small \lim\limits_{a\to-\infty} \displaystyle\int_{a}^{b}f(x)\mathrm dx$ , $\qquad \small\lim\limits_{b\to\infty} \displaystyle\int_{a}^{b}f(x)\mathrm dx\qquad$ oder $\small\qquad\lim\limits_{b\to\infty} \lim\limits_{a\to-\infty} \displaystyle\int_{a}^{b}f(x)\mathrm dx$

Berechnung

Um den Wert eines solchen Integrals zu berechnen, berechne das Integral wie gewohnt und behandle dabei die jeweilige Grenze, die gegen $\infty$ oder $-\infty$ läuft wie eine Variable. Vereinfache den Term auf diese Weise so weit wie möglich und bilde zum Schluss den Grenzwert.

Beispiel

$\begin{array}[t]{rll} \lim\limits_{a\to-\infty} \displaystyle\int_{a}^{2}\mathrm e^x\mathrm dx&= \end{array}$

Vollständige Lösung anzeigen

Der Graph der Funktion $f$ und die $x$ -Achse schließen eine ins Unendliche reichende Fläche ein, die entweder nach unten durch $a$ oder nach oben durch $b$ begrenzt ist.
Berechne deren endlichen Flächeninhalt.

$f\left(x\right)=\dfrac{1}{x^2}$
$a=1; \;\; b\to\infty$

$f\left(x\right)=\mathrm e^x$
$a\to-\infty; \;\; b=0$

$f\left(x\right)=-\dfrac{2}{x^2}$
$a\to-\infty; \;\; b=-1$

$f\left(x\right)=\dfrac{1}{2}x^{-5}$
$a\to-\infty;\;\; b=-2$

Gegeben ist die Funktion $f$ mit $f(x)=\dfrac{1}{\sqrt{x}}$ , sowie die Parallele zur $y$ -Achse $x=4$ .
Zeige auf, dass der Inhalt der ins Unendliche reichenden Fläche, die vom Graphen von $f$ und der Geraden mit der Gleichung $x=4$ eingeschlossen wird, keinen endlichen Wert annimmt.

Gegeben ist die Funktion $f$ mit $f(x)=-\mathrm{e}^2+\mathrm{e}^{2x}, \;\; x\in\mathbb{R}$ .

Skizziere das Schaubild von $f$ .

Berechne den Inhalt der Fläche, die vom Schaubild von $f$ und den Koordinatenachsen vollständig eingeschlossen wird.

Die waagerechte Asymptote des Schaubilds von $f$ hat die Gleichung $y=-\mathrm e^2$ . Gemeinsam mit den Koordinaten und dem Schaubild von $f$ schließt die Asymptote eine Fläche ein, die ins Unendliche reicht. Zeige, dass diese Fläche einen endlichen Flächeninhalt besitzt und berechne diesen.

Das Schaubild von $f$ und die Koordinatenachsen schließen eine ins Unendliche reichende Fläche ein. Berechne jeweils deren endlichen Flächeninhalt.

$f(x)=\mathrm{e}^{-2x}$

$f(x)=2\mathrm{e}^{-4x+1}$

$f(x)=3\mathrm{e}^{-3x+2}$

$f(x)=\mathrm{e}^{-x+1}$

Gegeben ist die Funktion $f(x)=-\mathrm{e}^{-2x}+1$ mit $x\in\mathbb{R}$

Skizziere das Schaubild von $f$ und gib eine Gleichung der waagerechten Asymptote von $f$ an.

Die $y$ -Achse, die waagerechte Asymptote, sowie das Schaubild von $f$ begrenzen eine nach rechts unbeschränkte Fläche. Zeige auf, dass der Inhalt dieser Fläche endlich ist und gib diesen an.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$\begin{array}{llllllll} A&=\left|\lim\limits_{b\to\infty}{\displaystyle\int\limits_1^{b}{\dfrac{1}{x^2}}\;\mathrm dx}\right|\\ A&=1\,FE \end{array}$

Vollständige Lösung anzeigen

$\begin{array}{llllllll} A&=\left|\lim\limits_{a\to-\infty}{\displaystyle\int\limits_a^{0}{\mathrm e^x}\;\mathrm dx}\right|\\[5pt] &=1\,FE \end{array}$

Vollständige Lösung anzeigen

$\begin{array}{llllllll} A&=\left|\lim\limits_{a\to-\infty}{\displaystyle\int\limits_a^{-1}{-\dfrac{2}{x^2}}\;\mathrm dx}\right|\\&=2\,FE \end{array}$

Vollständige Lösung anzeigen

$\begin{array}{rlllllll} A&=\left|\lim\limits_{a\to-\infty}{\displaystyle\int\limits_a^{-2}{\dfrac{1}{2}x^{-5}}\;\mathrm dx}\right|\\[5pt] &=\dfrac{1}{128}\,FE \end{array}$

Vollständige Lösung anzeigen

Berechne zunächst das Integral, das den Flächeninhalt $A$ der Fläche zwischen dem Graphen von f und der Parallel $x = 4$ in Abhängigkeit von $b$ beschreibt:

$\begin{array}{llllllll} A =\left|\displaystyle\int_{4}^{b}\dfrac{1}{\sqrt{x}}\;\mathrm dx\right|\\ =\left|2\cdot\sqrt{b}-4\right| \end{array}$

Vollständige Lösung anzeigen

Bilde nun den Grenzwert von A für $b\rightarrow{ }\infty$ um zu zeigen, dass diese Fläche keinen endlichen Wert besitzt.
Für $b\rightarrow{ }\infty$ strebt der Flächeninhalt $A=\left|2\cdot\sqrt{b}-4\right|$ gegen unendlich. Es existiert somit kein endlicher Flächeninhalt.

Punkte im Schaubild: $(0| -\mathrm{e}^2)$ , $(1 | 0)$

Graph einer mathematischen Funktion mit Koordinatensystem und Achsenbeschriftungen.

1. Schritt: Bestimmung der Integrationsgrenzen

Die Fläche wird durch die Schnittpunkte mit den Koordinatenachsen begrenzt. Nach links ist dies die Grenze $x=0$ .
Setze $f(x)=0$ , um die Schnittstelle mit der $x$ -Achse zu berechnen.

$\begin{array}{rllllllll} f(x)&=-\mathrm{e}^2+\mathrm{e}^{2x}=0\\&x=1 \end{array}$

Vollständige Lösung anzeigen

2. Schritt: Bestimmung des Flächeninhalts

$\begin{array}{rllllllll} A&=\left|\displaystyle\int_{0}^{1}\left(-\mathrm{e}^2+\mathrm{e}^{2x}\right)\;\mathrm dx\right|\\[5pt] &=\dfrac{1}{2}\mathrm{e}^2+\dfrac{1}{2} \end{array}$

Vollständige Lösung anzeigen

Der Flächeninhalt beträgt somit $A=\dfrac{1}{2}\mathrm{e}^2+\dfrac{1}{2}\approx4,2\,$ FE.

Der Flächeninhalt der ins Unendliche reichenden Fläche ergibt sich aus der Differenz der Geraden und der Funktion $f$ (obere Funktionen minus untere Funktionen).

$\begin{array}{lllllllll} A_{\infty} =\left|\dfrac{1}{2}-\dfrac{1}{2}\mathrm{e}^{2a}\right| \end{array}$

Vollständige Lösung anzeigen

Für $a\rightarrow{ }-\infty$ strebt $\left|\dfrac{1}{2}-\frac{1}{2}\mathrm{e}^{2a}\right|\rightarrow{ }\dfrac{1}{2}$ , da $\mathrm{e}^{2a}$ für $a\rightarrow{ }-\infty$ gegen $0$ geht.

Der Grenzwert der Fläche ist somit $\dfrac{1}{2}$ . Die ins Unendliche reichende Fläche hat den Flächeninhalt $A_{\infty}=\dfrac{1}{2}$ .

Alle Funktionen, deren Funktionsgleichung die Form $f(x)=e^-{ax}$ mit { $a>0$ } hat, haben die $y$ -Achse als waagerechte Asymptote, denn für $x\to\infty$ geht $f(x)\to0$ .
In allen vier Aufgabenteilen handelt es sich folglich um Flächen, die nach rechts ins Unendliche reichen. Nach links werden sie jeweils durch die y-Achse, also durch $x=0$ begrenzt.

$\begin{array}{rllllllll} A&=\left|\displaystyle\int_{0}^{b}\mathrm{e}^{-2x}\;\mathrm dx\right|\\[5pt] &=\left|-\dfrac{1}{2}\mathrm{e}^{-2b}+\dfrac{1}{2}\right| \end{array}$

Vollständige Lösung anzeigen

Für $b\rightarrow{ }\infty$ geht

$A=-\dfrac{1}{2}\mathrm{e}^{-2b}+\dfrac{1}{2}$ gegen $\dfrac{1}{2}$ .

Es ist damit $\mathop {\lim }\limits_{b \to \infty }A=\dfrac{1}{2}$ .

Der Flächeninhalt nimmt den

endlichen Wert A= $\dfrac{1}{2}$ FE an.

$\begin{array}{rllllllll} A&=\displaystyle\int_{0}^{b}2\mathrm{e}^{-4x+1}\\[5pt] &=-\dfrac{1}{2}\mathrm{e}^{-4b+1}+\dfrac{1}{2}\cdot\mathrm{e}^{1} \end{array}$

Vollständige Lösung anzeigen

Für $b\rightarrow{ }\infty$

geht $A=-\dfrac{1}{2}\mathrm{e}^{-4b+1}+\dfrac{1}{2}\cdot\mathrm{e}^{1}$

gegen $\dfrac{1}{2}\cdot\mathrm{e}$ .

Es ist damit $\mathop {\lim }\limits_{b \to \infty }A=\dfrac{1}{2}\cdot\mathrm{e}$

Der Flächeninhalt nimmt den

endlichen Wert $\dfrac{1}{2}\cdot\mathrm{e}$ FE an.

$\begin{array}{rllllllll} A&=\displaystyle\int_{0}^{b}3\mathrm{e}^{-3x+2}\;\mathrm dx\\[5pt] &=-\mathrm{e}^{-3b+2}+\mathrm{e}^2 \end{array}$

Vollständige Lösung anzeigen

Für $b\rightarrow{ }\infty$ geht $A=-\mathrm{e}^{-3b+2}+\mathrm{e}^2$ gegen $\mathrm{e}^2$ .

Es ist damit $\mathop {\lim }\limits_{b \to \infty }A=\mathrm{e}^2$ .

Der Flächeninhalt nimmt den

endlichen Wert $\mathrm{e}^2$ FE an.

$\begin{array}{rllllllll} A&=\displaystyle\int_{0}^{b}\mathrm{e}^{-x+1}\;\mathrm dx\\[5pt] &=\left[-\mathrm{e}^{-(x+1}\right]_0^b\\[5pt] &=-\mathrm{e}^{-b+1}+\mathrm{e}^{1} \end{array}$

Für $b\rightarrow{ }\infty$ geht $A=-\mathrm{e}^{-b+1}+\mathrm{e}^{1}$ gegen $\mathrm{e}$ .

Es ist damit $\mathop {\lim }\limits_{b \to \infty }A=\mathrm{e}.$

Der Flächeninhalt nimmt den

endlichen Wert $\mathrm{e}$ FE an.

Schaubild von f:

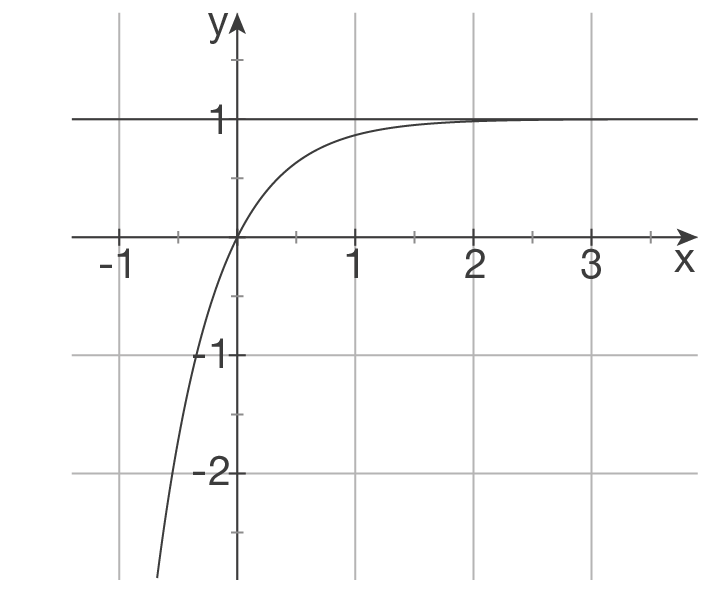Graph einer mathematischen Funktion im Koordinatensystem mit x- und y-Achse.

Waagerechte Asymptote des Schaubildes von $f$ :

Die waagerechte Asymptote des Schaubildes von $f$ ist

$y=1$ , da $-\mathrm{e}^{-2x}\rightarrow{ }0$ für $x\rightarrow{ }\infty$

und daher $f(x)=-\mathrm{e}^{-2x}+1\rightarrow{ }1$

für $x\rightarrow{ }\infty$ geht.

Die Schnittfläche der Asymptoten und des Schaubildes von $f$ reicht nach rechts ins Unendliche.

$\begin{array}{rllllllll} A&=\displaystyle\int_{0}^{b}(1-f(x))\;\mathrm dx\\[5pt] &=-\dfrac{1}{2}\mathrm{e}^{-2b}+\dfrac{1}{2} \end{array}$

Vollständige Lösung anzeigen

Für den Inhalt der nach rechts begrenzten Fläche gilt:

$A=\lim \limits_{a \to \infty } \left(-\dfrac{1}{2}\mathrm{e}^{-2b}+\dfrac{1}{2}\right)=\dfrac{1}{2}$ FE

Damit hat die beschriebene Fläche

den endlichen Inhalt von $\dfrac{1}{2}$ FE.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?