Gerade - Gerade
Mit dem Abstand zwischen zwei Geraden 
und 
ist der kürzeste Abstand zwischen diesen beiden Geraden gemeint. Um diesen bestimmen zu können, ist es zuerst nötig die gegenseitige Lage der Geraden zu kennen. Wir unterscheiden diese vier Möglichkeiten:
- Die beiden Geraden sind identisch
der Abstand ist null
- Die beiden Geraden schneiden sich
- Die beiden Geraden sind parallel
auf
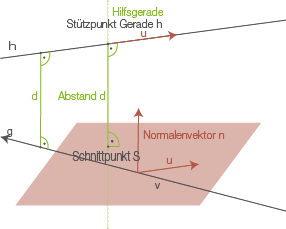
- Die beiden Geraden sind windschief
Vorgehen mit einer Hilfsebene
- Stelle eine Hilfsebene in Parameterform auf. Diese Hilfsebene enthält eine der Geraden
- Bestimme eine Hilfsgerade, die senkrecht auf der Hilfsebene steht und die andere Gerade
- Bestimme den Schnittpunkt der Hilfsgeraden und der Hilfsebene.
- Berechne den Abstand zwischen Schnittpunkt und dem Stützpunkt von
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
Zunächst muss man überprüfen, ob die Geraden parallel oder windschief sind. Dazu prüft man die Richtungsvektoren auf lineare Abhängig-bzw. Unabhängigkeit.
Dann hat man mehrere Möglichkeiten den Abstand zu berechnen.
Dann hat man mehrere Möglichkeiten den Abstand zu berechnen.
a)
Überprüfung, ob parallel oder windschief:
=
![\( \begin{array}{rlrl}
1=&2r&\quad \Rightarrow r=\dfrac{1}{2}
\\[5pt]
2=&0r&\quad \Rightarrow 2=0 & \text{keine Lösung}
\\[5pt]
0=&2r&\quad \Rightarrow 0=r
\end{array}\)](https://mathjax.schullv.de/51b601c15c7f184200a9a3b15e1ba2af6a74c800932c496c9b9a309b9625c35b?color=5a5a5a)
Die Richtungsvektoren sind somit linear unabhängig voneinander, demnach liegen die Geraden nicht parallel sondern windschief zueinander (da sie laut Aufgabenstellung entweder windschief oder parallel sind).
„Ersatzebene“ 
aufstellen mit den zwei Richtungsvektoren der Geraden:
=
Normalenvektor für Koordinatenform aufstellen:
=
=
=
in 
=
Hesse‘sche Normalenform 
aufstellen:
Der Abstand der beiden Geraden entspricht nun dem Abstand des Stützpunktes von zur Ebene . Um diesen zu bestimmen, werden die Koordinaten des Stützpunktes in die HNF eingesetzt:
=
=
=
.
Die beiden Geraden haben einen Abstand von 3 LE voneinander
Vollständige Lösung anzeigen
b)
Überprüfung, ob parallel oder windschief:
=
![\( \begin{array}{rlrl}
1=&0r&\quad \Rightarrow 1=0 &\text{keine Lösung}
\\[5pt]
1=&r&\quad \Rightarrow r=1
\\[5pt]
1=&2r&\quad \Rightarrow r=\frac{1}{2}
\end{array}\)](https://mathjax.schullv.de/d909d4ccee42ddd05aa767fa58db44046b0afc330e30cba4458f889c8aa00dda?color=5a5a5a)
Die Richtungsvektoren sind somit linear unabhängig voneinander,und windschief zueinander.
„Ersatzebene“ aufstellen mit den zwei Richtungsvektoren der Geraden:
=
Normalenvektor für Koordinatenform aufstellen:
=
=
in :
aufstellen:
Der Abstand des Stützvektors von zur Ebene entspricht dem Abstand der windschiefen Geraden:
=
=
=
c)
Überprüfung, ob parallel oder windschief:
=
Die Richtungsvektoren sind somit linear abhängig voneinander,und parallel zueinander.
Der Abstand des Stützvektors von zum Fußpunkt auf entspricht dem Abstand der beiden Geraden (vgl.Skript).
Fußpunkt welcher auf liegt bestimmen:
bestimmen:
=
=
Dieser Verbindungsvektor muss senkrecht zur Geraden stehen, sein Skalarprodukt muss mit dem Richtungsvektor der Geraden also Null ergeben:
![\( \begin{array}{rl}
-4+4t+4+16t=&0
\\[5pt]
20t=&0
\\[5pt]
t=&0
\end{array}\)](https://mathjax.schullv.de/73c85d6ebc983a34acc65b967aff359da75f2fd2150d6c15a4f1dab4975c443c?color=5a5a5a)
Dieser Wert liefert uns den gesuchten Verbindungsvektor . Der Betrag des Verbindungsvektors gibt uns also den Abstand der beiden parallelen Geraden an:
=
=
=
=
d)
Überprüfung, ob parallel oder windschief:
=
![\( \begin{array}{rlrl}
2=&2r&\quad \Rightarrow& r=1
\\[5pt]
-1=&r&\quad \Rightarrow& r=-1
\\[5pt]
-2=&4r&\quad \Rightarrow& r=-\frac{1}{2}
\end{array}\)](https://mathjax.schullv.de/e817b5153974f70af641a24a4b976a705463031c0740c7903cdaf90649721417?color=5a5a5a)
Die Richtungsvektoren sind somit linear unabhängig voneinander,und windschief zueinander.
„Ersatzebene“ aufstellen mit den zwei Richtungsvektoren der Geraden:
=
Normalenvektor für Koordinatenform aufstellen:
=
=
=
in 
aufstellen:
Der Abstand des Stützvektors von zur Ebene entspricht dem Abstand der windschiefen Geraden:
=
=
e)
Überprüfung, ob parallel oder windschief:
=
![\( \begin{array}{rlrl}
1=&0r&\quad \Rightarrow 1=0& \text{Widerspruch}
\\[5pt]
-2=&-2r&\quad \Rightarrow r=1
\\[5pt]
1=&r&\quad \Rightarrow r=1
\end{array}\)](https://mathjax.schullv.de/bf4d268f1ca8a82e76ddcffc7856943eabb4f7249f3e9e3ad656013a9fc92c89?color=5a5a5a)
Die Richtungsvektoren sind somit linear unabhängig voneinander, und windschief zueinander.
„Ersatzebene“ aufstellen mit den zwei Richtungsvektoren der Geraden:
=
Normalenvektor für Koordinatenform aufstellen:
=
=
=
in : 
aufstellen:
Der Abstand des Stützvektors von zur Ebene entspricht dem Abstand der windschiefen Geraden:
=
f)
Überprüfung, ob parallel oder windschief:
=
![\( \begin{array}{rlr}
4=&1r&\quad \Rightarrow r=4
\\[5pt]
0=&0r&\quad \Rightarrow 0=0
\\[5pt]
4=&1r&\quad \Rightarrow r=4
\end{array}\)](https://mathjax.schullv.de/82e400e70286fb87374cc05802e50d188295425db7f2fbc1e8922d4a75cbc93f?color=5a5a5a)
Die Richtungsvektoren sind somit linear abhängig voneinander,und parallel zueinander.
Der Abstand des Stützvektors von zum Fußpunkt auf entspricht dem Abstand der beiden Geraden.
Fußpunkt welcher auf liegt bestimmen:
bestimmen:
=
=
Das Skalarprodukt zwischen und dem Richtungsvektor von h muss gleich 
sein:
![\( \begin{array}{rl}
t+t-2=&0
\\[5pt]
2t=&2&
\\[5pt]
t=&1
\end{array}\)](https://mathjax.schullv.de/3deda40e70c94d9ff5bc26353e9080acceaab99768cb986aa9c09a6c09a9ee49?color=5a5a5a)
=
=
=
2.
a)
1. Schritt: Geradengleichung aufstellen
![\(\begin{array}{rll}
h:\overrightarrow{x}=&\overrightarrow{OA}+r\cdot\overrightarrow{AB}
\\[5pt]
\overrightarrow{x}=&\left(\begin{array}{r}
2\\
-3\\
-5\\
\end{array}\right)+s\cdot\left(\begin{array}{r}
0\\
2\\
8\\
\end{array}\right)
\end{array}\)](https://mathjax.schullv.de/7ad82115a888a00799f40dbc57f088f7bccd9b2b10e2a99e87dad8a2c6bc7646?color=5a5a5a)
2. Schritt: Gegenseitige Lage der Geraden prüfen
Die Richtungsvektoren der beiden Geraden sind linear abhängig:
=
und 
verlaufen also parallel. Wir bestimmen den Abstand des Stützvektors von zu der Geraden .
3. Schritt: Abstand von und bestimmen
Wir bestimmen den Abstand von 
von .
Jeder Punkt
, der auf liegt, hat die Koordinaten 
.
Wir bestimmen nun den Verbindungsvektor von 
und :
=
=
Dieser Verbindungsvektor muss senkrecht zur Geraden stehen, sein Skalarprodukt muss mit dem Richtungsvektor der Geraden also Null ergeben.
Dieser Wert eingesetzt in die Geradengleichung liefert uns den gesuchten Punkt , der auf liegt und zu den kleinsten Abstand hat:
.
Der Betrag des Verbindungsvektors von und gibt uns also den Abstand der beiden parallelen Geraden an:
=
=
=
=
Die beiden Geraden sind LE voneinander entfernt.
Jeder Punkt
b)
1. Schritt: Geradengleichung aufstellen
Der Richtungsvektor der 
-Achse lautet 
. Da parallel zu dieser Achse verläuft, lautet die Geradengleichung:
=
.
2. Schritt: Gegenseitige Lage der Geraden prüfen
Da die Richtungsvektoren von und nicht linear abhängig sind, sind die Geraden nicht parallel. Um nun zu prüfen, ob sie einen Schnittpunkt besitzen, oder ob sie windschief verlaufen setzen wir 
.
![\(\begin{array}{lrll}
Ⅰ&1=&s
\\[5pt]
Ⅱ&2+r=&1&\quad\scriptsize\mid -2
\\[5pt]
Ⅲ&-2+4r=&3&\quad\scriptsize\mid +2
\\[5pt]
\hline
Ⅰ&1=&s
\\[5pt]
Ⅱ&r=&-1
\\[5pt]
Ⅲ&4r=&5
\end{array}\)](https://mathjax.schullv.de/65898d91d3c7d4d4cec16f8be008db29848cce12eccba2209eb8528a2d080222?color=5a5a5a)
Aus Ⅱ ergibt sich 
, aus Ⅲ 
. Das Gleichungssystem besitzt keine Lösung und die Geraden keinen Schnittpunkt. Sie verlaufen windschief zueinander.
3. Schritt: Abstand von und bestimmen
Wir stellen die Gleichung einer Hilfsebene 
auf, die parallel zur verläuft und in der liegt. Als Spannvektoren für diese Ebene benutzen wir also die beiden Richtungsvektoren von und .
=
Nun bestimmen wir den Abstand des Stützvektors von und der Hilfsebene . Hierzu bestimmen wir die Hesseschen Normalenform von .
4. Schritt: Normalenvektor berechnen - Kreuzprodukt der Spannvektoren
=
=
Als vorläufige Normalenform ergibt sich also 
. Wir setzen die Koordinaten des Stützvektors von in die Gleichung ein, um 
zu bestimmen.
.
Damit lautet die Normalenform von 
. Für die hessesche Normalenform wird diese noch durch den Betrag des Normalenvektors geteilt:
=
Nun setzen wir den Punkt 
in diese Gleichung ein. Da und die Ebene parallel verlaufen, gibt uns der Abstand von zu auch den Abstand von zu .
=
Der Abstand der Geraden beträgt etwa 
LE.