Differenzierbarkeit
Eine Funktion  ist differenzierbar an der Stelle
ist differenzierbar an der Stelle  , falls der Grenzwert des Differenzenquotienten existiert. Dieser Grenzwert wird als Differentialquotient bezeichnet.
, falls der Grenzwert des Differenzenquotienten existiert. Dieser Grenzwert wird als Differentialquotient bezeichnet.
 Der Differentialquotient ist dann die Ableitung von
Der Differentialquotient ist dann die Ableitung von  an der Stelle
an der Stelle  .
Anschaulich bedeutet das, dass du an der Stelle
.
Anschaulich bedeutet das, dass du an der Stelle  eine eindeutige Tangente an die Funktion anlegen kannst. Die Funktion muss also stetig sein und darf keinen „Knick“ haben.
eine eindeutige Tangente an die Funktion anlegen kannst. Die Funktion muss also stetig sein und darf keinen „Knick“ haben.
 .
.
 =
= Falls du die Ableitung der Funktion kennst, kannst du auch folgende Gleichheit überprüfen:
Falls du die Ableitung der Funktion kennst, kannst du auch folgende Gleichheit überprüfen:

 differenzierbar ist:
differenzierbar ist: 
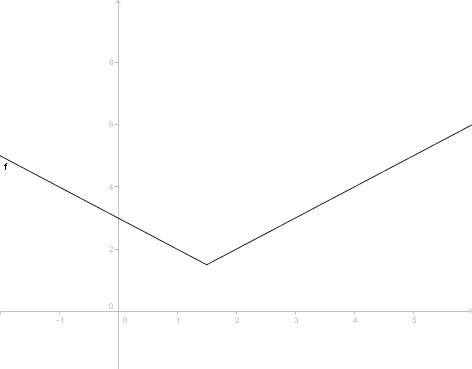 1. Schritt: Ableitung bilden
Du kannst die Funktion stückweise ableiten:
1. Schritt: Ableitung bilden
Du kannst die Funktion stückweise ableiten:
 2. Schritt: Werte der Ableitungsfunktion überprüfen
Die Funktion
2. Schritt: Werte der Ableitungsfunktion überprüfen
Die Funktion  , sowie die Funktion
, sowie die Funktion  sind differenzierbar. Somit musst du nur die Stelle
sind differenzierbar. Somit musst du nur die Stelle  auf Differenzierbarkeit prüfen.
auf Differenzierbarkeit prüfen.


 Die Funktion
Die Funktion  ist an der Stelle
ist an der Stelle  nicht differenzierbar.
nicht differenzierbar.
 -Methode, ob die Funktion
-Methode, ob die Funktion  differenzierbar ist.
differenzierbar ist.

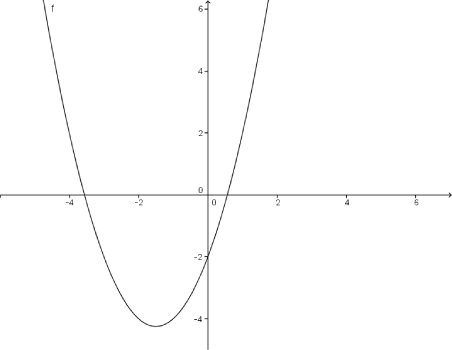 Der Differentialquotient existiert, somit ist die Funktion
Der Differentialquotient existiert, somit ist die Funktion  differenzierbar für
differenzierbar für  .
.
Funktion auf Differenzierbarkeit überprüfen
Um eine Funktion auf Differenzierbarkeit zu prüfen, betrachte den links- und den rechtsseitigen Grenzwert des Differenzenquotienten. Stimmen die Grenzwerte überein ist die Funktion differenzierbar an der StelleBeispiel 1
Überprüfe ob die Funktion
Beispiel 2
Überprüfe, mithilfe der
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
Eine kurze Beschreibung fur den Begriff Differenzierbarkeit wiedergeben
Eine differenzierbare Funktion ist zum einen stetig und darf zum anderen keinen Knick enthalten. An einem Knick könnte man nämlich keine Tangenten anlegen, da sich an dieser Stelle keine eindeutige Steigung finden lassen würde.
2.
Die Funktion auf Differenzierbarkeit untersuchen
 1. Schritt: Steigung betrachten
1. Schritt: Steigung betrachten
 Ableitungsfunktion bestimmen:
Ableitungsfunktion bestimmen:
 für
für  gilt:
gilt:
![\(\begin{array}[t]{p{1cm}rl}
&
1
&
=1
\\
&
2\cdot\dfrac{1}{2}
&
=1
\end{array}\)](https://mathjax.schullv.de/62f8277314760897673e727eee98757b7046652baa3fadced9b0acdbd4845dc6?color=5a5a5a) Die Funktion weist an der Stelle
Die Funktion weist an der Stelle  die selbe Steigung auf.
die selbe Steigung auf.
 2. Schritt:
2. Schritt:  -Werte betrachten
-Werte betrachten
 für
für  gilt:
gilt:
![\(\begin{array}[t]{p{1cm}rl}
&
\dfrac{1}{2}-2
&
=-\dfrac{3}{2}
\\
&
-7+\dfrac{1}{4}
&
=-\dfrac{27}{4}
\end{array}\)](https://mathjax.schullv.de/e74fca7072454a23618194fb5cd2e80686352aa4e0f3ae8d8e8d8454a346c3a3?color=5a5a5a) Die Funktion weist an der Stelle
Die Funktion weist an der Stelle  verschiedene Y-Werte auf.
verschiedene Y-Werte auf.
 Die Funktion ist nicht differenzierbar.
Die Funktion ist nicht differenzierbar.
 Steigung betrachten
Steigung betrachten
 Ableitungsfunktion bestimmen:
Ableitungsfunktion bestimmen:
 für
für  gilt:
gilt:
![\(\begin{array}[t]{p{1cm}rl}
&
3^{2}
&
=9
\\
&
2
&
=2
\end{array}\)](https://mathjax.schullv.de/1685ba5de62bc99e1e1466522f2ec33c7c65892d1813a6943b408bd7260c0636?color=5a5a5a) Die Funktion weist an der Stelle
Die Funktion weist an der Stelle  nicht die selbe Steigung auf.
nicht die selbe Steigung auf.
 Die Funktion ist nicht differenzierbar.
Die Funktion ist nicht differenzierbar.
 1. Schritt: Steigung betrachten
1. Schritt: Steigung betrachten
 Ableitungsfunktion bestimmen:
Ableitungsfunktion bestimmen:
 für
für  gilt:
gilt:
![\(\begin{array}[t]{p{1cm}rl}
&
\dfrac{1}{2}
&
=\dfrac{1}{2}
\\
&
2\cdot2-3,5
&
=\dfrac{1}{2}
\end{array}\)](https://mathjax.schullv.de/15ff253e6ed98772341c3c24f9db315f283a0dc87917561bbd446d9792e4a30d?color=5a5a5a) Die Funktion weist an der Stelle
Die Funktion weist an der Stelle  die selbe Steigung auf.
die selbe Steigung auf.
 2. Schritt:
2. Schritt:  -Werte betrachten
für
-Werte betrachten
für  gilt:
gilt:
![\(\begin{array}[t]{p{1cm}rl}
&
\dfrac{1}{2}\cdot2+1
&
=2
\\
&
4-7+5
&
=2
\end{array}\)](https://mathjax.schullv.de/c59581b87cd78fb76d1ed80aa3e080c02a7260a47df67c9a61c632c3dba52871?color=5a5a5a) Die Funktion weist an der Stelle
Die Funktion weist an der Stelle  gleiche Y-Werte auf.
gleiche Y-Werte auf.
 Die Funktion ist differenzierbar.
Die Funktion ist differenzierbar.
a)
b)
c)
3.
s und t so bestimmen, dass die Funktion an der Stelle  differenzierbar ist
differenzierbar ist
 1. Schritt: Steigung betrachten
1. Schritt: Steigung betrachten
 Ableitungsfunktion bestimmen:
Ableitungsfunktion bestimmen:
 für
für  gilt:
gilt:
![\(\begin{array}[t]{p{1cm}rl}
&
2t\cdot1-1
&
=m
\\
&
-2\cdot1
&
=-2
\end{array}\)](https://mathjax.schullv.de/7f781d8cfacd69975f84639c1a13bc78053ce1a65381c18c1fdc95dd4d542bd6?color=5a5a5a) Da bei differenzierbaren Funktionen m an der gesuchten Stelle
Da bei differenzierbaren Funktionen m an der gesuchten Stelle  gleich sein muss gilt:
gleich sein muss gilt:
![\(\begin{array}[t]{p{1cm}rl}
&
m
&
=-2
\\
&
2t\cdot1-1
&
=-2
\\
&
-\dfrac{1}{2}
&
=t
\end{array}\)](https://mathjax.schullv.de/ecbf76a890d0ebd5b44d1a0c4796600266f09acd9eab1a4354c00b0fdcdccb0b?color=5a5a5a)
 2. Schritt:
2. Schritt:  -Werte berachten
-Werte berachten
 für
für  gilt:
gilt:
![\(\begin{array}[t]{p{1cm}rl}
&
-\dfrac{1}{2}-1+s
&
=Y
\\
&
-1+1
&
=0
\end{array}\)](https://mathjax.schullv.de/20623a61a4116aad9e08bc007db9ac4ab03588b2694be2a13865c7739ae9bca7?color=5a5a5a) Da bei differenzierbaren Funktionen der
Da bei differenzierbaren Funktionen der  -Wert an der gesuchten Stelle
-Wert an der gesuchten Stelle  gleich sein muss gilt:
gleich sein muss gilt:
![\(\begin{array}[t]{p{1cm}rl}
&
Y
&
=0
\\
&
-\dfrac{1}{2}-1+s
&
=0
\\
&
\dfrac{3}{2}
&
=s
\end{array}\)](https://mathjax.schullv.de/82841d9d52a2b23d447c99168136f65f135edb8849d49887ce319533205ad911?color=5a5a5a) Die Funktion ist für
Die Funktion ist für  und für
und für  differenzierbar.
differenzierbar.