Exponentialfunktionen
1.
Das Schaubild der Funktion  mit
mit  stellt den Gewinn einer Firma dar, die aufgrund negativer Publicity und einiger Affären in Bezug auf Geldwäsche plötzlich kollabiert ist. Die Stelle
stellt den Gewinn einer Firma dar, die aufgrund negativer Publicity und einiger Affären in Bezug auf Geldwäsche plötzlich kollabiert ist. Die Stelle  kennzeichnet hierbei das Jahr 2000, eine LE auf der
kennzeichnet hierbei das Jahr 2000, eine LE auf der  -Achse steht für ein Jahr, eine LE auf der
-Achse steht für ein Jahr, eine LE auf der  -Achse steht für 100.000€.
-Achse steht für 100.000€.
a)
Skizziere das Schaubild von  in einem Koordinatensystem.
in einem Koordinatensystem.
b)
In welchem Jahr fiel der Gewinn um 300.000€?
c)
Wann machte die Firma den maximalen Gewinn?
d)
Bestimme den Bereich, in dem der Gewinn stetig gestiegen ist.
2.
Eine Gebirgslandschaft lässt sich durch das Schaubild der Funktion  mit
mit  beschreiben. (1 LE
beschreiben. (1 LE 
 m)
m)
Das Schaubild der Funktion mit
mit  beschreibt die Flugbahn eines Heißluftballons.
beschreibt die Flugbahn eines Heißluftballons.
Das Schaubild der Funktion
a)
Skizziere die Schaubilder beider Funktionen in einem Koordinatensystem.
b)
Bestimme den höchsten Punkt des Gebirges.
c)
Bestimme den Abstand, den der Heißluftballon von diesem Punkt hat, wenn er gerade darüber hinweg fliegt.
d)
Bei  befindet sich am Gebirge eine Aussichtsplattform, die rechtwinklig zum Gebirge gebaut wurde. Bei
befindet sich am Gebirge eine Aussichtsplattform, die rechtwinklig zum Gebirge gebaut wurde. Bei  steht ein 1,80m großer Mann auf der Plattform. Bestimme den Abstand, den der Heißluftballon von dem Mann hat, wenn er direkt über ihn hinweg fliegt.
steht ein 1,80m großer Mann auf der Plattform. Bestimme den Abstand, den der Heißluftballon von dem Mann hat, wenn er direkt über ihn hinweg fliegt.
3.
Der Querschnitt eines Walls wird durch das Schaubild der Funktion  mit
mit  beschrieben.
beschrieben.
An der rechten Seite schließt sich direkt ein Meer an, das durch die -Achse beschrieben werden kann.
-Achse beschrieben werden kann.
Bevor der Wall aufgeschüttet wurde, befand sich hier lediglich ein kleiner Anstieg, der durch das Schaubild der Funktion mit
mit  beschrieben werden kann.
beschrieben werden kann.
An der rechten Seite schließt sich direkt ein Meer an, das durch die
Bevor der Wall aufgeschüttet wurde, befand sich hier lediglich ein kleiner Anstieg, der durch das Schaubild der Funktion
a)
Skizziere die Schaubilder beider Funktionen in einem Koordinatensystem.
b)
Wie hoch ist der Wall an der höchsten Stelle?
c)
Zur Befestigung wurde bei  ein Stahlpfeiler hinabgelassen, der senkrecht zur Oberfläche des Walls steht. An welcher Stelle ist der Pfeiler auf dem ehemaligen Anstieg befestigt?
ein Stahlpfeiler hinabgelassen, der senkrecht zur Oberfläche des Walls steht. An welcher Stelle ist der Pfeiler auf dem ehemaligen Anstieg befestigt?
d)
Wo muss sich auf dem Meer ein Schiff befinden, damit man es von der Stelle  aus sehen kann?
aus sehen kann?
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
Das Schaubild der Funktion  mit
mit  stellt den Gewinn einer Firma dar, die aufgrund negativer Publicity und einiger Affären in Bezug auf Geldwäsche plötzlich kollabiert ist. Die Stelle
stellt den Gewinn einer Firma dar, die aufgrund negativer Publicity und einiger Affären in Bezug auf Geldwäsche plötzlich kollabiert ist. Die Stelle  kennzeichnet hierbei das Jahr 2000, eine LE steht für ein Jahr, eine LE auf der
kennzeichnet hierbei das Jahr 2000, eine LE steht für ein Jahr, eine LE auf der  -Achse steht für 100.000 €.
-Achse steht für 100.000 €.
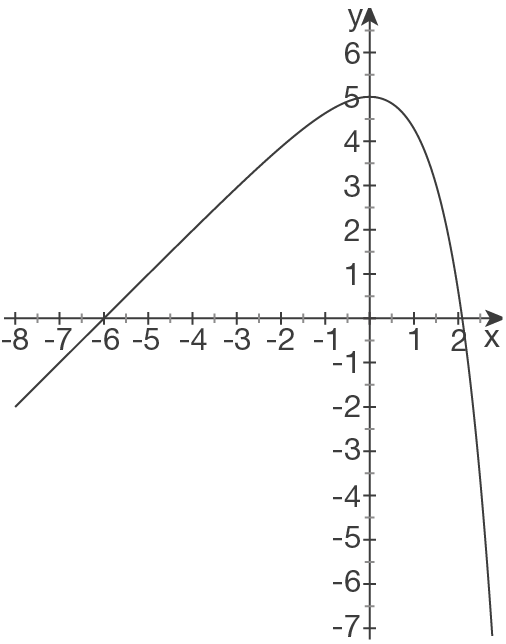
a)

b)
Hier ist nach der Änderungsrate gefragt. Es soll bestimmt werden, an welcher Stelle  die Steigung bei
die Steigung bei  € pro Jahr lag.
€ pro Jahr lag.
Die Änderungsrate bestimmen wir immer mit der ersten Ableitung. Da eine LE auf der -Achse 100.000 € darstellt, werden -300.000 also durch die -3 dargestellt.
-Achse 100.000 € darstellt, werden -300.000 also durch die -3 dargestellt.
Wir setzen also und lösen die Gleichung nach
und lösen die Gleichung nach  auf.
auf.
 bestimmen
Ableitung bilden
bestimmen
Ableitung bilden
![\(\begin{array}{rlll}
f\left(x\right)&=-\mathrm e^x+x+6\\[3pt]
f‘\left(x\right)&=-\mathrm e^x+1
\end{array}\)](https://mathjax.schullv.de/d7811fe7f60a1237c50ec3389df9a9c539b6d09fba636458119f6015aab0a4df?color=5a5a5a)
 setzen
setzen
![\(\begin{array}{rllll}
-\mathrm e^x+1&=-3&\scriptsize{\mid\;-1}\\[3pt]
-\mathrm e^x&=-4&\scriptsize{\mid\;\cdot\left(-1\right)}\\[3pt]
\mathrm e^x&=4&\scriptsize{\mid\;\ln{\left(\;\right)}}\\[3pt]
\ln{\left(\mathrm e^x\right)}&=\ln{\left(4\right)}\\[3pt]
x&=\ln\left(4\right)\\[3pt]
x\approx 1,386
\end{array}\)](https://mathjax.schullv.de/6407c4eff2c9c6afaf1cd385ec4b7c7a1d0f1de536228c7320d73fe3160ed96d?color=5a5a5a) Am Anfang des Jahres 2001 fiel der Gewinn um 300.000 €.
Am Anfang des Jahres 2001 fiel der Gewinn um 300.000 €.
Die Änderungsrate bestimmen wir immer mit der ersten Ableitung. Da eine LE auf der
Wir setzen also
c)
Um den maximalen Gewinn der Firma zu bestimmen, bestimmen wir das Maximum von  . Dazu setzen wir
. Dazu setzen wir  .
Maximum von
.
Maximum von  bestimmen
bestimmen

 setzen
setzen
![\(\begin{array}{rlll}
-\mathrm e^x+1&=0&\scriptsize{\mid\;-1}\\[3pt]
-\mathrm e^x&=-1&\scriptsize{\mid\;\cdot\left(-1\right)}\\[3pt]
\mathrm e^x&=1&\scriptsize{\mid\;\ln{\left(\;\right)}}\\[3pt]
\ln{\left(\mathrm e^x\right)}&=\ln{\left(1\right)}\\[3pt]
x&=0
\end{array}\)](https://mathjax.schullv.de/0d2a7232c63408ebc00b2faf428db1699c3f2be3e6708126e5d123247d1cf71c?color=5a5a5a)
 auf echtes Maximum überprüfen
auf echtes Maximum überprüfen
 An der Stelle
An der Stelle  , also im Jahr 2000 hat die Firma den größten Gewinn gemacht.
, also im Jahr 2000 hat die Firma den größten Gewinn gemacht.
d)
Hier soll  auf Monotonie überprüft werden. Wir wissen, dass das Schaubild von
auf Monotonie überprüft werden. Wir wissen, dass das Schaubild von  bis zum Hochpunkt steigt und dann fällt.
Die
bis zum Hochpunkt steigt und dann fällt.
Die  -Koordinate des Hochpunktes ist uns bereits bekannt, nämlich
-Koordinate des Hochpunktes ist uns bereits bekannt, nämlich  . Somit können wir sagen:
. Somit können wir sagen:
 ist monoton steigend für
ist monoton steigend für  .
.
2.
Eine Gebirgslandschaft lässt sich durch die Funktion  mit
mit  beschreiben. (1 LE
beschreiben. (1 LE 
 m)
Die Funktion
m)
Die Funktion  beschreibt die Flugbahn eines Heißluftballons.
beschreibt die Flugbahn eines Heißluftballons.
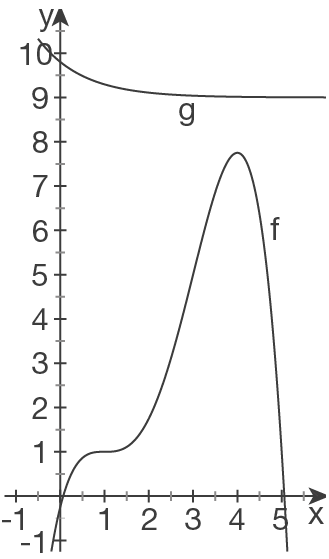
a)

b)
Der höchste Punkt des Gebirges ist der Hochpunkt des Schaubildes von  .
Hochpunkt des Schaubildes von
.
Hochpunkt des Schaubildes von  bestimmen
Ableitungen bilden
bestimmen
Ableitungen bilden
![\(\begin{array}{rllll}
f\left(x\right)&=-\dfrac{1}{4}\left(x-1\right)^4+\left(x-1\right)^3+1\\[5pt]
f‘\left(x\right)&=-\dfrac{1}{4}\cdot4\left(x-1\right)^3+3\left(x-1\right)^2\\[5pt]
&=-\left(x-1\right)^3+3\left(x-1\right)^2\\[5pt]
f‘‘\left(x\right)&=-3\left(x-1\right)^2+3\cdot2\left(x-1\right)\\[5pt]
&=-3\left(x-1\right)^2+6\left(x-1\right)
\end{array}\)](https://mathjax.schullv.de/fb0127d8a340cd5afb4ffef8823b08adf226e326c751d395aefea3fea3997510?color=5a5a5a)
 setzen
Ein Produkt ist
setzen
Ein Produkt ist  , wenn einer seiner Faktoren
, wenn einer seiner Faktoren  ist:
ist:
![\(\begin{array}{rllll}
\left(x-1\right)^2&=0&\scriptsize{\mid\;\sqrt{\;}}\\[3pt]
x-1&=0&\scriptsize{\mid\;+1}\\[3pt]
x_1&=1\\[5pt]
-x+4&=0&\scriptsize{\mid\;+x}\\[3pt]
4=x_2
\end{array}\)](https://mathjax.schullv.de/bc742b30fd10a163e1affb0e81fafe5a4383cda97131e2fa34fa643e8ea4cd10?color=5a5a5a)
 auf echtes Maximum überprüfen
auf echtes Maximum überprüfen
![\(\begin{array}{rllll}
f‘‘\left(1\right)&=-3\left(1-1\right)^2+6\left(1-1\right)\\[3pt]
f‘‘\left(1\right)&=0&
\end{array}\)](https://mathjax.schullv.de/3ee1b49818b2c6d675c584fc4444925e50f68ddc0b6843c68ed473ce2c90bcb6?color=5a5a5a) Für
Für  kann noch nicht eindeutig gesagt werden, ob
kann noch nicht eindeutig gesagt werden, ob  eine Extremstelle ist. Überprüfe zunächst die andere mögliche Extremstelle. Ist diese eine Maximalstelle, dann kann
eine Extremstelle ist. Überprüfe zunächst die andere mögliche Extremstelle. Ist diese eine Maximalstelle, dann kann  keine mehr sein, da es nur zwei mögliche Extremstellen gibt, und zwischen zwei Maxima auch immer ein Minimum liegen muss.
keine mehr sein, da es nur zwei mögliche Extremstellen gibt, und zwischen zwei Maxima auch immer ein Minimum liegen muss.
 auf echtes Maximum überprüfen
auf echtes Maximum überprüfen
 -Wert von
-Wert von  bestimmen
bestimmen
![\(\begin{array}{rllll}
f\left(4\right)&=-\dfrac{1}{4}\left(4-1\right)^4+\left(4-1\right)^3+1\\[5pt]
&=-\dfrac{1}{4}\cdot3^4+3^3+1\\[5pt]
&=-\dfrac{1}{4}\cdot81+27+1\\[5pt]
&=-20,25+28\\[5pt]
&=7,75
\end{array}\)](https://mathjax.schullv.de/6989f34ab4b9486d277d28ec380557a6e2279c264f30f10dd0c9ff138f9d663d?color=5a5a5a) Der höchste Punkt des Gebirgszugs ist
Der höchste Punkt des Gebirgszugs ist  .
.
c)
Wir wissen nun, dass sich der höchste Punkt bei  befindet. Wir bestimmen nun also die Höhe des Heißluftballons an der Stelle
befindet. Wir bestimmen nun also die Höhe des Heißluftballons an der Stelle  und messen dann die Differenz der beiden Werte.
Höhendifferenz bestimmen
und messen dann die Differenz der beiden Werte.
Höhendifferenz bestimmen
 bestimmen
bestimmen
![\(\begin{array}{rllll}
g\left(4\right)&=\dfrac{1}{25}\mathrm e^{-4+3}+9\\[5pt]
&=\dfrac{1}{25}\mathrm e^{-1}+9\\[5pt]
&=\dfrac{1}{25}\cdot\dfrac{1}{\mathrm e}+9\\[5pt]
&=0,015+9\\[5pt]
g\left(4\right)&=9,015
\end{array}\)](https://mathjax.schullv.de/fe520101527eae15e75c03c7cd05dfe3396e88178b4eb60b3a4c0b0ca6d6b9e7?color=5a5a5a) Differenz berechnen
Differenz berechnen
 Eine Längeneinheit steht für
Eine Längeneinheit steht für  m. Deshalb beträgt der Abstand vom Heißluftballon zum Gipfel des Berges
m. Deshalb beträgt der Abstand vom Heißluftballon zum Gipfel des Berges  m.
m.
d)
Die Aussichtsplattform wurde rechtwinklig zum Gebirge gebaut. Wir können also die Gleichung der Normalen an der Stelle  bestimmen.
bestimmen.
Mit Hilfe dieser Gleichung können wir dann auch den Abstand zwischen Heißluftballon und dem Mann ausrechnen. Gleichung der Normalen bei bestimmen
Höhendifferenz bestimmen
bestimmen
Höhendifferenz bestimmen
 bestimmen
bestimmen
![\(\begin{array}{rll{\hspace{1cm}}l}
n:y&=0,163\cdot4,8+5,625\\[3pt]
&=0,7824+5,625\\[3pt]
&\approx 6,4
\end{array}\)](https://mathjax.schullv.de/11cbae3a5ab06a371b6b7941806fed594e162eef958f969c6d8695bb911b813e?color=5a5a5a)
 bestimmen
bestimmen
![\(\begin{array}{rll{\hspace{1cm}}l}
g\left(4,8\right)&=\dfrac{1}{25}\mathrm e^{-4,8+3}+9\\[5pt]
&=\dfrac{1}{25}\mathrm e^{-1,8}+9\\[5pt]
&=0,0067+9\\[3pt]
g\left(4,8\right)&\approx 9
\end{array}\)](https://mathjax.schullv.de/a5f1319499b2411414890203d713f32d3060b5b0d106d3a72bea03b976a0779f?color=5a5a5a) Der Mann ist
Der Mann ist  m groß, zur Höhe der Plattform muss also noch
m groß, zur Höhe der Plattform muss also noch  addiert werden.
Höhe des Mannes berechnen
addiert werden.
Höhe des Mannes berechnen
 Höhendifferenz berechnen
Höhendifferenz berechnen
 Der Heißluftballon ist
Der Heißluftballon ist  m von dem Mann entfernt.
m von dem Mann entfernt.
Mit Hilfe dieser Gleichung können wir dann auch den Abstand zwischen Heißluftballon und dem Mann ausrechnen. Gleichung der Normalen bei
3.
Der Querschnitt eines Walls wird durch das Schaubild der Funktion  mit
mit  beschrieben.
beschrieben.
An der rechten Seite schließt sich direkt ein Meer an, das durch die -Achse beschrieben werden kann.
Bevor der Wall aufgeschüttet wurde, befand sich hier lediglich ein kleiner Anstieg, der durch das Schaubild der Funktion
-Achse beschrieben werden kann.
Bevor der Wall aufgeschüttet wurde, befand sich hier lediglich ein kleiner Anstieg, der durch das Schaubild der Funktion  mit
mit  beschrieben werden kann.
beschrieben werden kann.
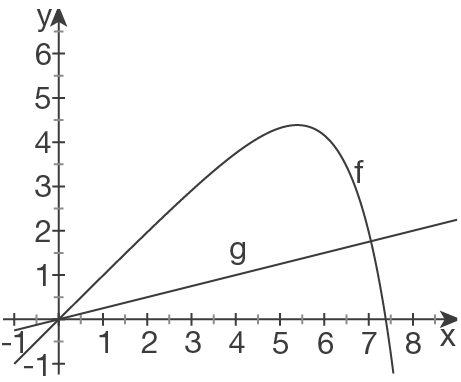
An der rechten Seite schließt sich direkt ein Meer an, das durch die
a)

b)
Hochpunkt des Schaubildes von  bestimmen
Ableitungen bilden
bestimmen
Ableitungen bilden
![\(\begin{array}{rllll}
f\left(x\right)&=x-\dfrac{1}{4}\mathrm e^{x-4}\\[5pt]
f‘\left(x\right)&=1-\dfrac{1}{4}\mathrm e^{x-4}\\[5pt]
f‘‘\left(x\right)&=-\dfrac{1}{4}\mathrm e^{x-4}
\end{array}\)](https://mathjax.schullv.de/3fcf77a0ba64e1823c80ce8c4593e155c66119d40fe4ca4d9a099c56c20b47fb?color=5a5a5a)
 setzen
setzen
![\(\begin{array}{rllll}
1-\dfrac{1}{4}\mathrm e^{x-4}&=0&\scriptsize{\mid\;+\dfrac{1}{4}\mathrm e^{x-4}}\\[5pt]
1&=\dfrac{1}{4}\mathrm e^{x-4}&\scriptsize{\mid\;\cdot4}\\[5pt]
4&=\mathrm e^{x-4}&\scriptsize{\mid\;\ln{\left(\;\right)}}\\[5pt]
\ln{\left(4\right)}&=\ln{\left(\mathrm e^{x-4}\right)}\\[5pt]
\ln{\left(4\right)}&=x-4&\scriptsize{\mid\;+4}\\[5pt]
\ln{\left(4\right)}+4&=x
\end{array}\)](https://mathjax.schullv.de/11ec0444da7b97889d868fd2e7407a0ffdec8214111eec3952eb3c19a2c3a0ce?color=5a5a5a)
 auf echtes Maximum prüfen
auf echtes Maximum prüfen
 -Wert zu
-Wert zu  bestimmen
Daraus ergibt sich der höchste Punkt des Walls
bestimmen
Daraus ergibt sich der höchste Punkt des Walls  .
.
c)
Der Pfeiler ist senkrecht zur Oberfläche des Walls eingelassen. Dies legt nahe, dass wir hier die Normale in dem Punkt bestimmen müssen.
Normale durch  bestimmen
Schnittpunkt der Normalen mit dem Schaubild von
bestimmen
Schnittpunkt der Normalen mit dem Schaubild von  bestimmen
bestimmen
![\(\begin{array}{rllll}
-1,1x+6,208&=\dfrac{1}{4}x&\scriptsize{\mid\;+1,1x}\\[5pt]
6,208&=1,35x&\scriptsize{\mid\;:1,35}\\[5pt]
4,6&\approx x
\end{array}\)](https://mathjax.schullv.de/4efb2e3924e628079b109da2616c150ab0e4499676aac1a1aa5b91438da6764a?color=5a5a5a)
 -Wert von
-Wert von  bestimmen
bestimmen
![\(\begin{array}{rllll}
g\left(4,6\right)&=\dfrac{1}{4}\cdot4,6\\[5pt]
g\left(4,6\right)&=1,15\\[5pt]
4,6&\approx x
\end{array}\)](https://mathjax.schullv.de/809ccf18f29128cda045122d4827c45e2e76eeace54902355e6ddcd8ef28fdfd?color=5a5a5a) Der Pfeiler ist etwa bei
Der Pfeiler ist etwa bei  im ehemaligen Anstieg befestigt.
im ehemaligen Anstieg befestigt.
d)
Hier ist gefragt, welchen Punkt auf dem Meer, d.h. auf der  -Achse, man von
-Achse, man von  aus gerade noch sehen kann.
aus gerade noch sehen kann.
Wir müssen also eine Tangente an der Stelle anlegen.
Tangentengleichung bestimmen
Schnittstelle der Tangente mit der
anlegen.
Tangentengleichung bestimmen
Schnittstelle der Tangente mit der  -Achse bestimmen
Ein Schiff muss sich mindestens an der Stelle
-Achse bestimmen
Ein Schiff muss sich mindestens an der Stelle  befinden, damit es auf dem Wall von der Stelle
befinden, damit es auf dem Wall von der Stelle  aus gesehen werden kann.
aus gesehen werden kann.
Wir müssen also eine Tangente an der Stelle