Input-Output-Tabelle
Aufbau einer Input-Output Tabelle
Wir wollen eine Input-Output Tabelle erstellen, die Informationen über einen Produktionsprozess liefert. In die Spalten dieser Tabelle kommen die Inputfaktoren, die im Zuge der Produktion verbraucht, verarbeitet oder umgewandelt werden. In die Zeilen kommen die Outputfaktoren, die im Laufe des Produktionsprozesses entstehen. Am Ende der Tabelle können noch Spalten hinzugefügt werden, falls beispielsweise einige der Zwischenprodukten an den Markt zurückgegeben werden. Schließlich wird die letzte Spalte mit dem Namen Gesamtproduktion erstellt. Diese beinhaltet die Summe aller einzelnen Outputfaktoren, die im Laufe des Produktionsprozesses entstehen. Die Werte der Tabelle geben uns die Information wie viele Einheiten von einer Abteilung an die anderen Abteilungen abgegeben worden sind. Stimmen die beiden Abteilungen überein, so spricht man vom Eigenbedarf der jeweiligen Abteilung. Die Spalte „Markt“ gibt uns einen Vektor, der Marktabgabenvektor genannt wird. Die Spalte „Gesamtproduktion“ gibt uns einen Vektor, der Produktionsvektor genannt wird. Die Werte der Vektoren ließt man den Spalten ab.Beispiel
Zwei Abteilungen| Output\Input | Abteilung A |
|---|---|
| Abteilung A | |
| Abteilung B |
1.
Drei Sektoren  ,
,  und
und  sind nach dem Leontief-Modell miteinander verflochten. Alle Lieferungen an den Markt und untereinander sowie die Produktion wird in Geldeinheiten (GE) angegeben. Zu den drei Sektoren sind folgende Informationen in der Produktionsperiode Ⅰ bekannt:
sind nach dem Leontief-Modell miteinander verflochten. Alle Lieferungen an den Markt und untereinander sowie die Produktion wird in Geldeinheiten (GE) angegeben. Zu den drei Sektoren sind folgende Informationen in der Produktionsperiode Ⅰ bekannt:
- Sektor
produziert insgesamt Waren im Wert von 24 Geldeinheiten. Davon wird ein Drittel zum Eigenbedarf verwendet, ein weiteres Drittel wird an den Sektor
geliefert und das übrige Drittel wird an den Markt abgegeben.
- Sektor
liefert insgesamt 15 GE. Davon werden Waren vom gleichen Wert an Sektor
und
weitergegeben, 6 GE decken den Eigenbedarf und 3 GE werden an den Markt geliefert.
- Sektor
deckt mit 2 GE den Eigenbedarf, liefert jeweils 3 GE an
, 4 GE an
und gibt Waren im Wert von 9 GE an den Markt ab.
a)
Stelle die zugehörige Input-Output-Tabelle auf und gib Produktions- und Marktabgabevektor an.
b)
In der zweiten Produktionsperiode soll die Gesamtproduktion aller Sektoren und 50 % erhöht werden. Dabei soll nur der Eigenbedarf aller Sektoren variiert werden.
Gib den Produktionsvektor  an und stelle die Input-Output-Tabelle der Produktionsperiode Ⅱ auf.
an und stelle die Input-Output-Tabelle der Produktionsperiode Ⅱ auf.
2.
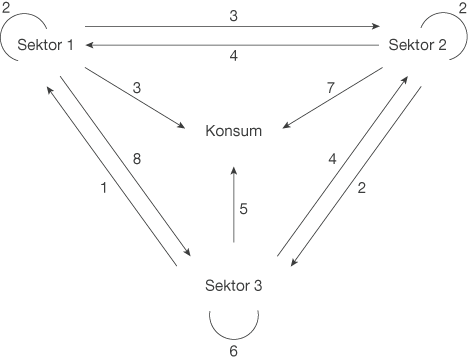
Betrachte den folgenden Verflechtungsgraphen, in welchem die Güterströme einer Firma mit 3 Sektoren dargestellt ist. Die einzelnen Sektoren sind jeweils für eine Gütersorte zuständig, die an die anderen Sektoren weitergegeben werden.
 Gib eine gleichwertige Darstellung als Input-Output-Tabelle an.
Gib eine gleichwertige Darstellung als Input-Output-Tabelle an.

Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
Input-Output-Tabelle aufstellen
Eine Input-Output-Tabelle stellt das Produktionsverhalten verschiedener Sektoren und deren Verflechtung untereinander dar.
Die Zeilen der Input-Output-Tabelle enthalten Informationen darüber, wie die produzierte Ware jedes Sektors verwendet wird. Bei diesem Anteil spricht man vom sogenannten „Output“.
In den Spalten kannst du dahingegen ablesen, welche „Inputs“ für die Produktion benötigt werden.
Eine solche Tabelle hat beispielsweise folgende Darstellung:
Hierbei wurden die drei gegebenen Sektoren  ,
,  und
und  bereits eingetragen. Beachte, dass die Einträge in der Spalte Gesamtproduktion aus der Zeilensumme über die Werte der Spalten „Sektoren&ldquo und „Markt“ hervorgeht.
Um die Input-Output-Tabelle zum gegebenen Sachverhalt aufzustellen, kannst du die im Aufgabentext genannten Informationen eintragen und anschließend vervollständigen.
1. Schritt: Informationen zu Sektor
bereits eingetragen. Beachte, dass die Einträge in der Spalte Gesamtproduktion aus der Zeilensumme über die Werte der Spalten „Sektoren&ldquo und „Markt“ hervorgeht.
Um die Input-Output-Tabelle zum gegebenen Sachverhalt aufzustellen, kannst du die im Aufgabentext genannten Informationen eintragen und anschließend vervollständigen.
1. Schritt: Informationen zu Sektor  eintragen
Laut Aufgabentext produziert
eintragen
Laut Aufgabentext produziert  insgesamt Waren im Wert von 24 GE. Das heißt, dass in der ersten Zeile unter Gesamtproduktion der Wert 24 eingetragen werden muss.
Weiterhin weißt du, dass ein Drittel dieser Gesamtproduktion zum Eigenbedarf verwendet wird, ein weiteres Drittel an
insgesamt Waren im Wert von 24 GE. Das heißt, dass in der ersten Zeile unter Gesamtproduktion der Wert 24 eingetragen werden muss.
Weiterhin weißt du, dass ein Drittel dieser Gesamtproduktion zum Eigenbedarf verwendet wird, ein weiteres Drittel an  und eines an den Markt gegeben wird. Folglich kannst du in jede dieser Zellen der Wert
und eines an den Markt gegeben wird. Folglich kannst du in jede dieser Zellen der Wert  eintragen.
Der Sektor
eintragen.
Der Sektor  erhält von
erhält von  keinen Input und wir schreiben in der verbleibenden Zelle den Wert 0.
Insgesamt erhalten wir dann folgende Darstellung:
keinen Input und wir schreiben in der verbleibenden Zelle den Wert 0.
Insgesamt erhalten wir dann folgende Darstellung:
2. Schritt: Informationen zu Sektor  eintragen
Analog verfahren wir mit den Einträgen in der Zeile zu Sektor
eintragen
Analog verfahren wir mit den Einträgen in der Zeile zu Sektor  .
.
Gegeben ist eine Gesamtproduktion von 15 GE. 6 GE werden zur Deckung des Eigenbedarfs verwendet und 3 GE werden an den Markt gegeben. Außerdem weißt du, dass Waren vom gleichen Wert an die Sektoren
an die Sektoren  und
und  weitergegeben werden.
weitergegeben werden.
Da sich der Wert der Gesamtproduktion aus der Summe über alle Werte der Sektoren und des Marktes zusammensetzt, kannst du folgende Gleichung aufstellen:
![\(\begin{array}{rll}
15&=&x+6+x+3 \\[5pt]
15&=&2\cdot x+9&\scriptsize{\; \mid\;-9} \\[5pt]
6&=&2\cdot x&\scriptsize{\; \mid\; :2} \\[5pt]
3&=& x
\end{array}\)](https://mathjax.schullv.de/dbad937ac463a80cbf4c344840990c1a8723494f412b7966bea5d5b1fceb05fd?color=5a5a5a) 3. Schritt: Informationen zu Sektor
3. Schritt: Informationen zu Sektor  eintragen
Es heißt: „Sektor
eintragen
Es heißt: „Sektor  deckt mit 2 GE den Eigenbedarf, liefert jeweils 3 GE an
deckt mit 2 GE den Eigenbedarf, liefert jeweils 3 GE an  , 4 GE an
, 4 GE an  und gibt Waren im Wert von 9 GE an den Markt ab“. Diese Angaben kannst du direkt eintragen und erhältst:
und gibt Waren im Wert von 9 GE an den Markt ab“. Diese Angaben kannst du direkt eintragen und erhältst:
Auch hier kannst du folgende Tatsache verwenden: Der Wert der Gesamtproduktion setzt sich aus der Summe über alle Werte der Sektoren und des Marktes zusammen. Folglich gilt für den Wert  der Gesamtproduktion:
der Gesamtproduktion:
![\(\begin{array}{rll}
y&3+4+2+9 \\[5pt]
y&18 \\
\end{array}\)](https://mathjax.schullv.de/a4b5b6640a6c869b7b0413c5072cfc88ceeddeb78e822d5e6921645f2672125b?color=5a5a5a) Damit sieht die vollständige Tabelle wie folgt aus:
Damit sieht die vollständige Tabelle wie folgt aus:
Produktions- und Marktabgabevektor angeben
Nachdem du die Input-Output-Tabelle aufgestellt hast, kannst du Produktions- und Marktabgabevektor direkt ablesen. Die Einträge des Marktabgabevektors  entsprechen gerade den Einträgen der rot gefärbten Spalte:
entsprechen gerade den Einträgen der rot gefärbten Spalte:
Damit lautet der Marktabgabevektor:  .
Die Einträge des Produktionsvektors
.
Die Einträge des Produktionsvektors  entsprechen hier den Einträgen der blau gefärbten Spalte:
entsprechen hier den Einträgen der blau gefärbten Spalte:
Damit lautet der Produktionsvektor:  .
.
| Input Output | Sektor |
Sektor |
| Sektor |
||
| Sektor |
||
| Sektor |
| Input Output | Sektor |
Sektor |
| Sektor |
8 | 0 |
| Sektor |
||
| Sektor |
Gegeben ist eine Gesamtproduktion von 15 GE. 6 GE werden zur Deckung des Eigenbedarfs verwendet und 3 GE werden an den Markt gegeben. Außerdem weißt du, dass Waren vom gleichen Wert
| Input Output | Sektor |
Sektor |
Sektor |
| Sektor |
6 |
| Input Output | Sektor |
Sektor |
Sektor |
| Sektor |
3 | 4 | 2 |
| Input Output | Sektor |
Sektor |
Sektor |
| Sektor |
8 | 0 | 8 |
| Sektor |
3 | 6 | 3 |
| Sektor |
3 | 4 | 2 |
| Input Output | Sektor |
Sektor |
Sektor |
| Sektor |
8 | 0 | 8 |
| Sektor |
3 | 6 | 3 |
| Sektor |
3 | 4 | 2 |
| Input Output | Sektor |
Sektor |
Sektor |
| Sektor |
8 | 0 | 8 |
| Sektor |
3 | 6 | 3 |
| Sektor |
3 | 4 | 2 |
b)
Input-Output-Tabelle der zweiten Produktionsperiode aufstellen
Ausgehend von den zuvor betrachteten Angaben soll nun in der zweiten Produktionsperiode die Gesamtproduktion in allen Sektoren um 50 % erhöht werden. Das heißt, der Produktionsvektor  soll mit dem Faktor 1,5 multipliziert werden und wir erhalten den neuen Produktionsvektor
soll mit dem Faktor 1,5 multipliziert werden und wir erhalten den neuen Produktionsvektor  :
:
 Deine Aufgabe ist es nun, die Input-Output-Tabelle für den neuen Produktionsvektor
Deine Aufgabe ist es nun, die Input-Output-Tabelle für den neuen Produktionsvektor  anzupassen, indem du nur den Eigenbedarf der Sektoren variierst.
Der zu variierende Eigenbedarf der einzelnen Sektoren entspricht gerade den rot markierten Zellen:
anzupassen, indem du nur den Eigenbedarf der Sektoren variierst.
Der zu variierende Eigenbedarf der einzelnen Sektoren entspricht gerade den rot markierten Zellen:
Die Werte  ,
,  , und
, und  kannst du anpassen, indem du verwendest, dass sich der Wert der Gesamtproduktion aus dem Output der Sektoren und dem Markt zusammensetzt. Dadurch erhältst du folgendes lineares Gleichungssystem:
kannst du anpassen, indem du verwendest, dass sich der Wert der Gesamtproduktion aus dem Output der Sektoren und dem Markt zusammensetzt. Dadurch erhältst du folgendes lineares Gleichungssystem:
 Damit hast du die gesuchten Werte für den Eigenbedarf ermittelt und kannst die Input-Output-Tabelle für die zweite Produktionsperiode wie folgt aufstellen:
Damit hast du die gesuchten Werte für den Eigenbedarf ermittelt und kannst die Input-Output-Tabelle für die zweite Produktionsperiode wie folgt aufstellen:
| Input Output | Sektor |
Sektor |
| Sektor |
0 | |
| Sektor |
3 | |
| Sektor |
3 | 4 |
| Input Output | Sektor |
Sektor |
Sektor |
| Sektor |
20 | 0 | 8 |
| Sektor |
3 | 13,5 | 3 |
| Sektor |
3 | 4 | 11 |
2.
Betrachte den folgenden Verflechtungsgraphen, in welchem die Güterströme einer Firma mit 3 Sektoren dargestellt sind. Die einzelnen Sektoren sind jeweils für eine Gütersorte zuständig, die an die anderen Sektoren weitergegeben wird.
 Die Zeilen der Input-Output-Tabelle enthalten Informationen darüber, wie die produzierte Ware jedes Sektors verwendet wird. Bei diesem Anteil spricht man vom sogenannten „Output“.
Die Zeilen der Input-Output-Tabelle enthalten Informationen darüber, wie die produzierte Ware jedes Sektors verwendet wird. Bei diesem Anteil spricht man vom sogenannten „Output“.
In den Spalten kannst du dahingegen ablesen, welche „Inputs“ für die Produktion benötigt werden. Eine gleichwertige Input-Output-Tabelle hat beispielsweise folgende Darstellung:
Wir zeigen hier das Übertragen in eine Input-Output-Tabelle anhand des 1. Sektors. Bei diesem entsprechen alle Pfeile, die auf andere Einheiten zeigen, dem Output, welcher zeilenweise eingetragen wird. Pfeile, die dahingegen auf den 1. Sektor zeigen, entsprechen dem Input, der spaltenweise eingetragen wird.
Die Werte über den Pfeilen im Verflechtungsgraphen stellen jeweils die Geldeinheiten dar, in welchen die Ware gemessen wird. Betrachtest du nun Sektor 1, so kannst du feststellen, dass 2 GE für den Eigenbedarf verwendet werden, 3 GE an Sektor 2 und 8 GE an Sektor 3 abgegeben werden. Weiterhin werden noch 3 GE zum Konsum freigegeben.
Durch diese Angaben kannst du nun die erste Zeile der Tabelle ausfüllen und erhältst:
Verfahre so mit den anderen beiden Sektoren, sodass du folgende Input-Output-Tabelle hast:
Zuletzt fehlen nur noch die Einträge in der Spalte zur Gesamtproduktion. Da sich die Werte der Gesamtproduktion aus der Zeilensumme berechnet, kannst du die vollständige Input-Output-Tabelle angeben mit:

In den Spalten kannst du dahingegen ablesen, welche „Inputs“ für die Produktion benötigt werden. Eine gleichwertige Input-Output-Tabelle hat beispielsweise folgende Darstellung:
| Input Output | Sektor 1 | Sektor 2 | Sektor 3 |
| Sektor 1 | |||
| Sektor 2 | |||
| Sektor 3 |
Die Werte über den Pfeilen im Verflechtungsgraphen stellen jeweils die Geldeinheiten dar, in welchen die Ware gemessen wird. Betrachtest du nun Sektor 1, so kannst du feststellen, dass 2 GE für den Eigenbedarf verwendet werden, 3 GE an Sektor 2 und 8 GE an Sektor 3 abgegeben werden. Weiterhin werden noch 3 GE zum Konsum freigegeben.
Durch diese Angaben kannst du nun die erste Zeile der Tabelle ausfüllen und erhältst:
| Input Output | Sektor 1 | Sektor 2 | Sektor 3 |
| Sektor 1 | 2 | 3 | 8 |
| Input Output | Sektor 1 | Sektor 2 | Sektor 3 |
| Sektor 1 | 2 | 3 | 8 |
| Sektor 2 | 4 | 2 | 2 |
| Sektor 3 | 1 | 4 | 6 |
| Input Output | Sektor 1 | Sektor 2 | Sektor 3 |
| Sektor 1 | 2 | 3 | 8 |
| Sektor 2 | 4 | 2 | 2 |
| Sektor 3 | 1 | 4 | 6 |