Exponentialfunktionen
Exponentialfunktionen sind Funktionen der Form:

 wird als Basis bezeichnet und
wird als Basis bezeichnet und  als Exponent.
Hast du eine solche Funktion gegeben, kannst du beim Skizzieren des Graphen entweder eine Wertetabelle anlegen oder dich an einer Grundfunktion orientieren.
als Exponent.
Hast du eine solche Funktion gegeben, kannst du beim Skizzieren des Graphen entweder eine Wertetabelle anlegen oder dich an einer Grundfunktion orientieren.
 Es handelt sich hier um eine veränderte
Es handelt sich hier um eine veränderte  -Funktion. Du kannst den Funktionsterm zunächst umformen:
-Funktion. Du kannst den Funktionsterm zunächst umformen:
 Mit der Berechnung der Schnittpunkte mit den Koordinatenachsen erhältst du folgende Informationen:
Mit der Berechnung der Schnittpunkte mit den Koordinatenachsen erhältst du folgende Informationen:
 also aus dem Graph der
also aus dem Graph der  -Funktion durch Spiegelung an der
-Funktion durch Spiegelung an der  -Achse und der
-Achse und der  -Achse, anschließende Streckung in
-Achse, anschließende Streckung in  -Richtung um den Faktor
-Richtung um den Faktor  und Verschiebung um eine Einheit in positive
und Verschiebung um eine Einheit in positive  -Richtung (nach oben).
-Richtung (nach oben).
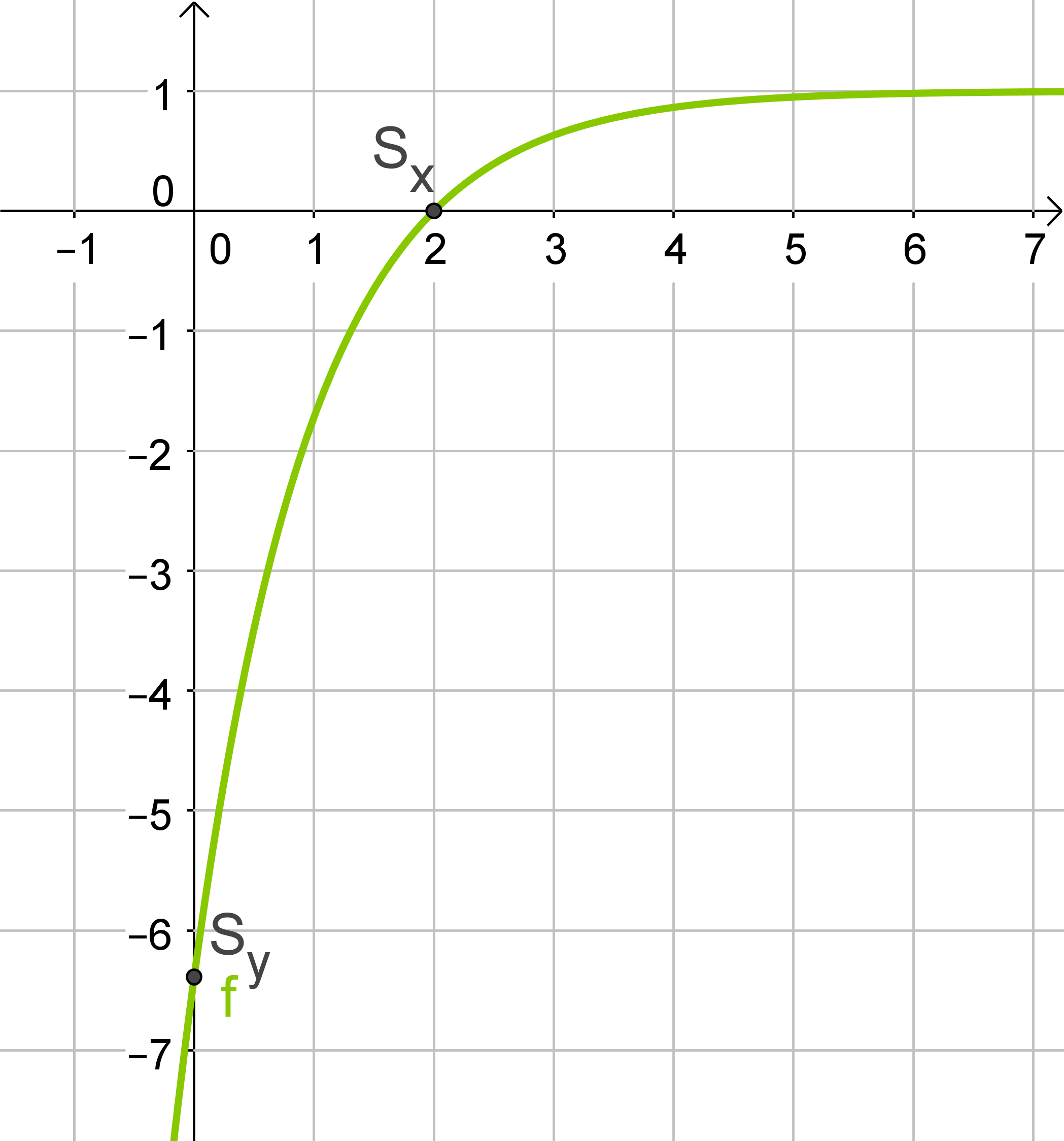
Beispiel
Gegeben:- Der Graph zu
entsteht durch Spiegelung des Graphen von
an der
-Achse.
- Der Graph zu
entsteht durch Spiegelung des Graphen von
an der
-Achse.
- Der Faktor
führt zu einer Streckung des Graphen in
-Richtung.
- Der Summand
im Funktionsterm bewirkt eine Verschiebung des Graphen im Koordinatensystem um
Einheit nach oben.
Der Graph nähert sich also für große Werte der waagerechten Asymptotean.
- Schnittpunkte mit den Achsen:
und

1.
Skizziere die Schaubilder folgender Funktionen und bestimme die Gleichung der Asymptote.






a)
b)
c)
d)
e)
f)
2.
Skizziere das Schaubild der Funktion und beschreibe, wie es aus dem Schaubild der  -Funktion hervorgeht.
-Funktion hervorgeht.






a)
b)
c)
d)
e)
f)
3.
Verschiebe das Schaubild der angegebenen Funktion wie gefordert und gib die Funktionsgleichung der neuen Funktion an.
 Verschiebung um 2 LE in positive x-Richtung („nach rechts“) und um 2 LE in positive y-Richtung („nach oben“)
Verschiebung um 2 LE in positive x-Richtung („nach rechts“) und um 2 LE in positive y-Richtung („nach oben“)
 Verschiebung um 2 LE in negative x-Richtung („nach links“) und um 1 LE in positive y-Richtung („nach oben“)
Verschiebung um 2 LE in negative x-Richtung („nach links“) und um 1 LE in positive y-Richtung („nach oben“)
 Verschiebung um 1 LE in negative x-Richtung („nach links“) und um 4 LE in negative y-Richtung („nach unten“)
Verschiebung um 1 LE in negative x-Richtung („nach links“) und um 4 LE in negative y-Richtung („nach unten“)
 Verschiebung um 2 LE in positive y-Richtung („nach oben“) und anschließende Spiegelung an der x-Achse
Verschiebung um 2 LE in positive y-Richtung („nach oben“) und anschließende Spiegelung an der x-Achse
 Verschiebung um 3 LE in positive x-Richtung („nach rechts“) und anschließende Spiegelung an der y-Achse
Verschiebung um 3 LE in positive x-Richtung („nach rechts“) und anschließende Spiegelung an der y-Achse
 Verschiebung um 4 LE in positive y-Richtung („nach oben“) und um 3 LE in negative x-Richtung („nach links“)
Verschiebung um 4 LE in positive y-Richtung („nach oben“) und um 3 LE in negative x-Richtung („nach links“)
a)
b)
c)
d)
e)
f)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
Skizze
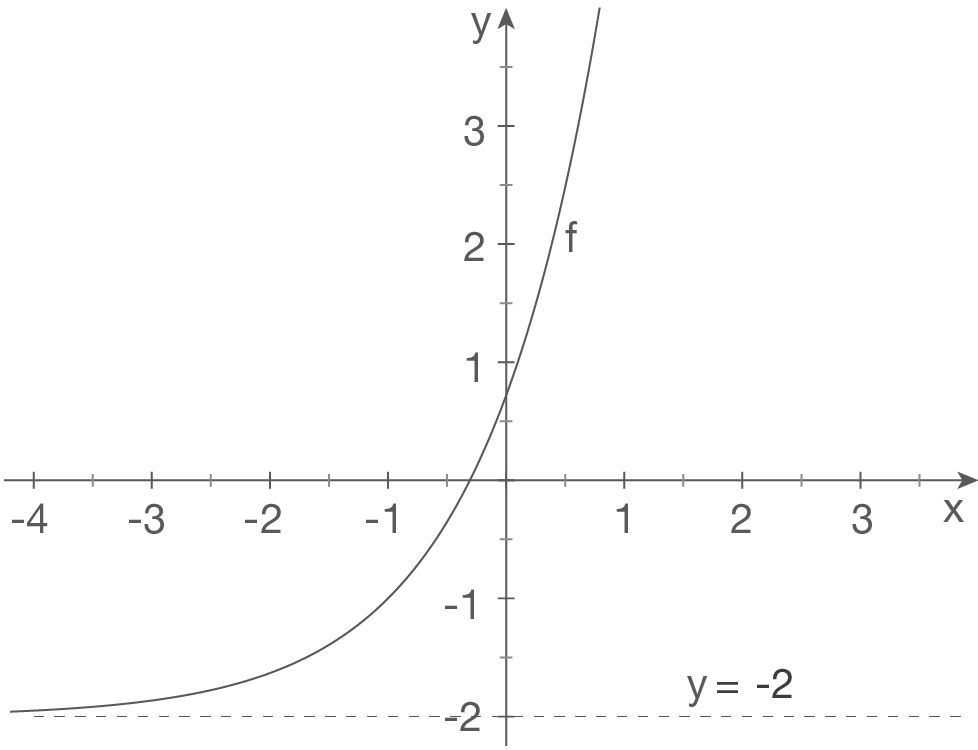
Wir betrachten den Grenzwert von
Für
b)
Skizze
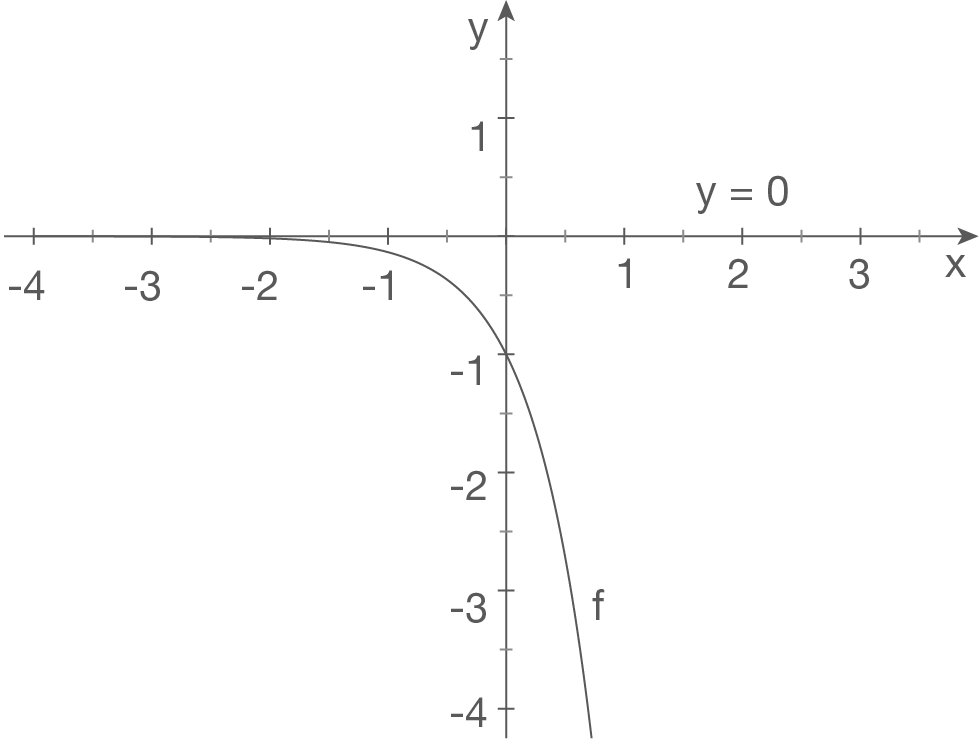
Wir betrachten den Grenzwert von
Für
c)
Skizze
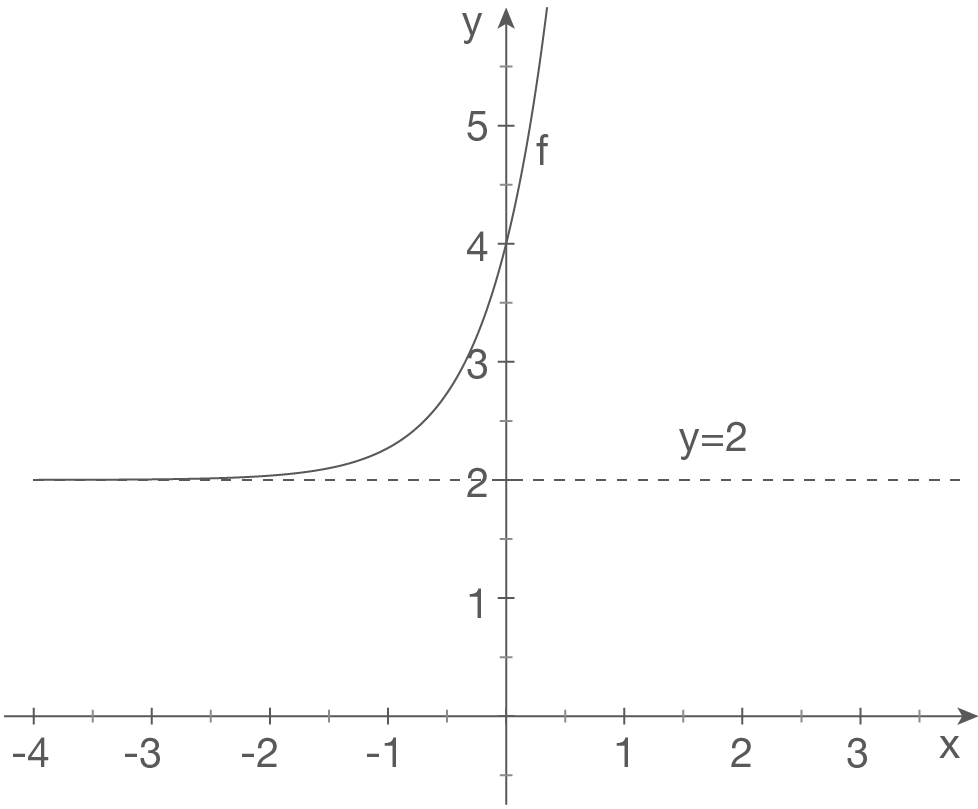
Wir betrachten den Grenzwert von
d)
Skizze
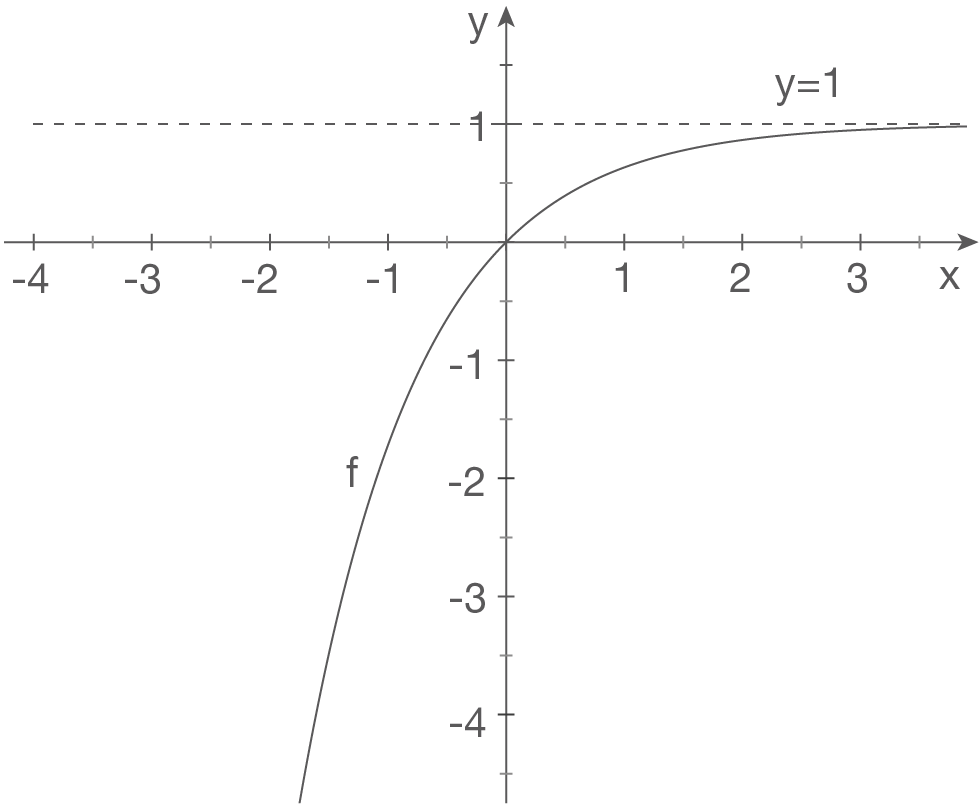
Wir betrachten den Grenzwert von
e)
Skizze
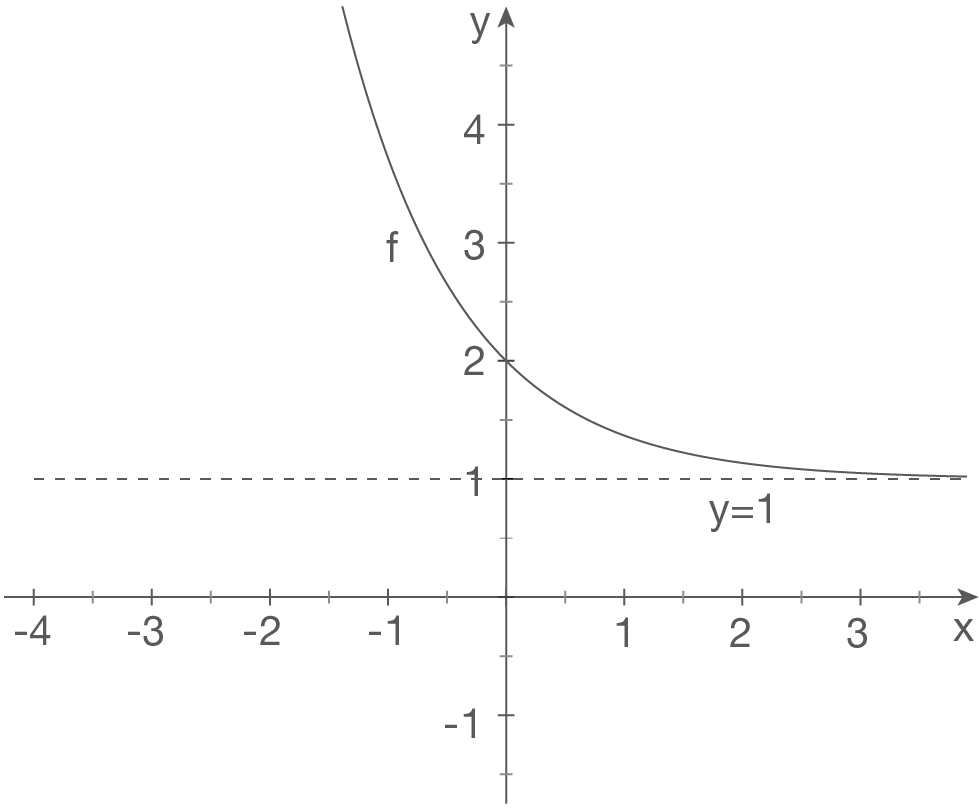
Wir betrachten den Grenzwert von
f)
Skizze
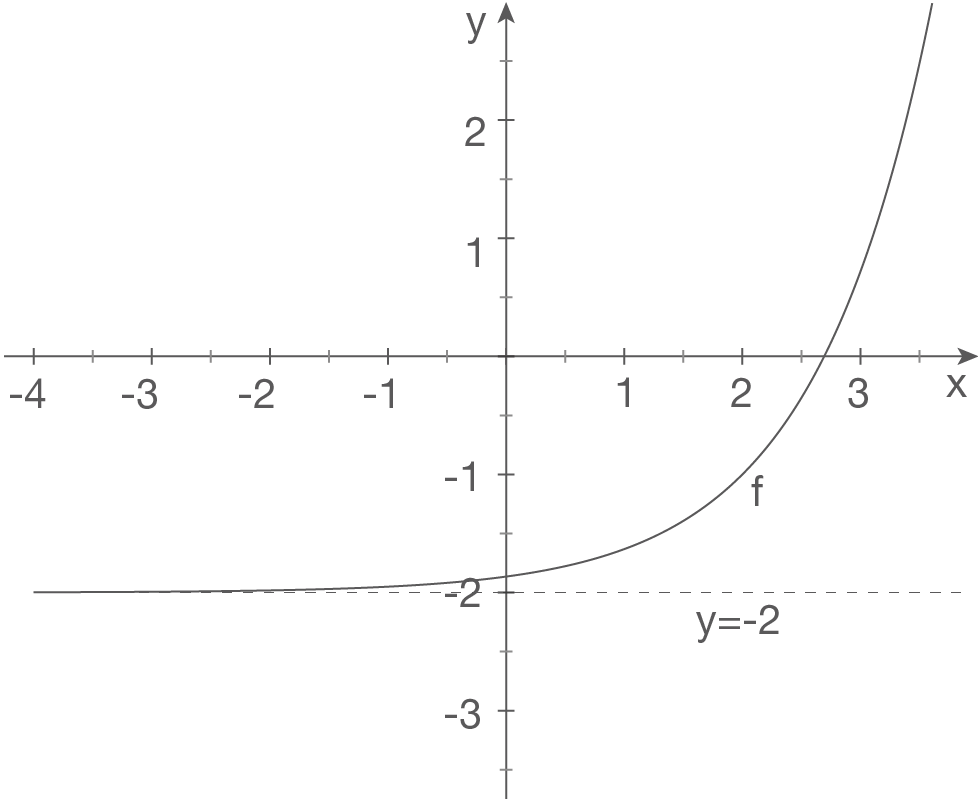
Wir betrachten den Grenzwert von
2.
a)
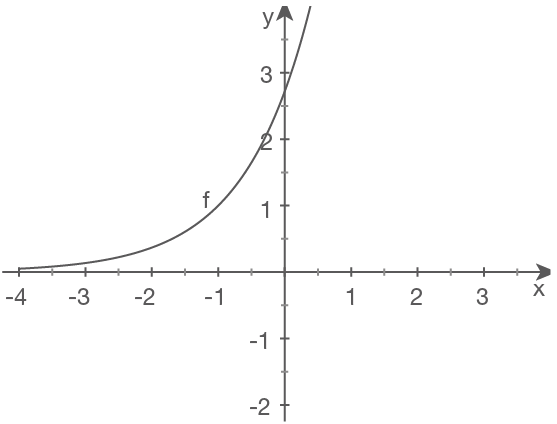
b)
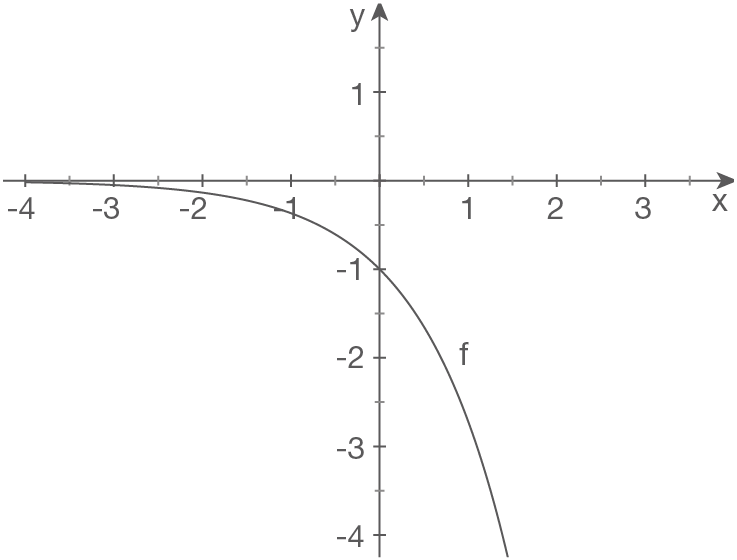
c)
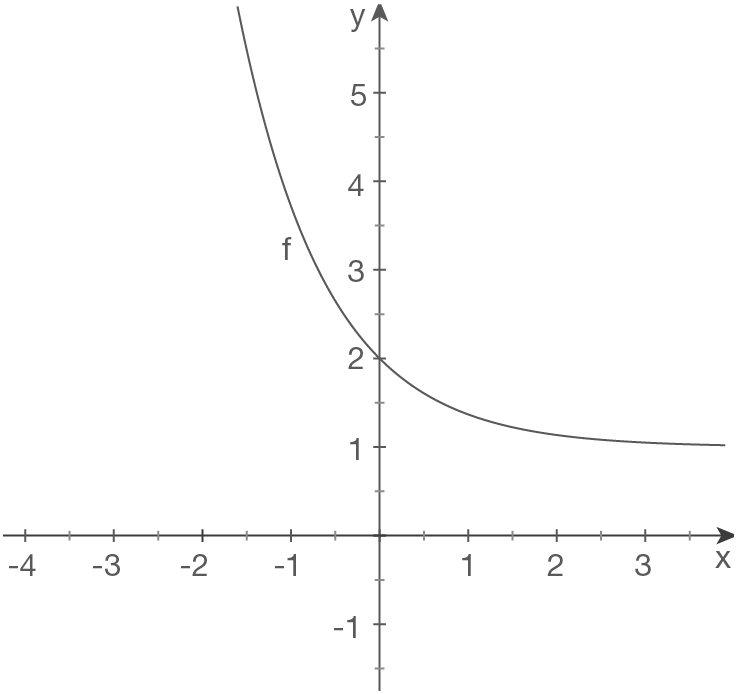
d)
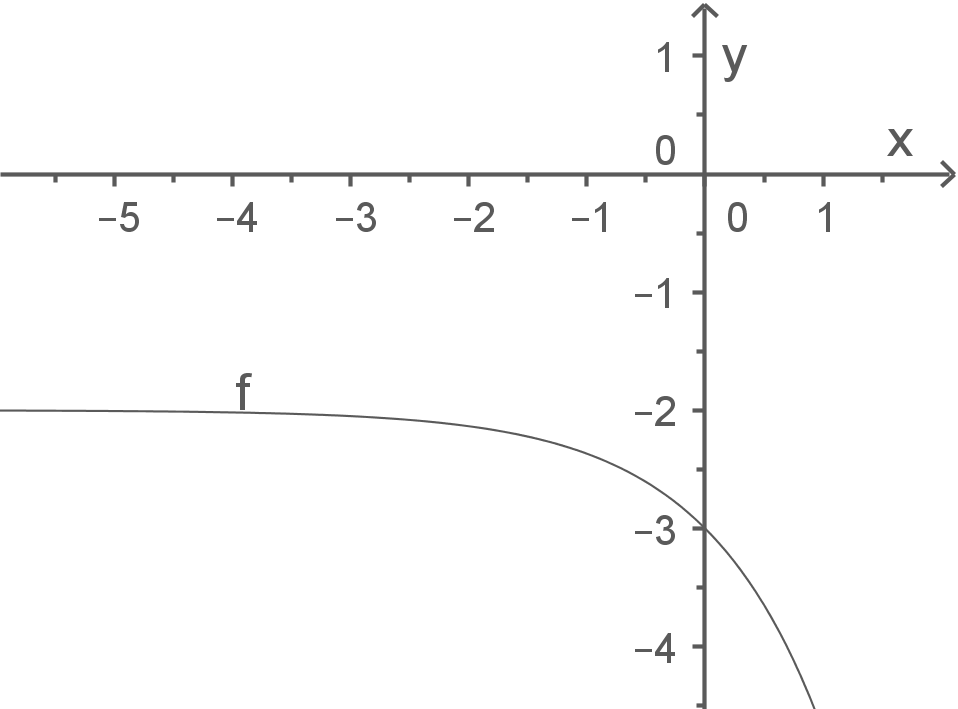
e)
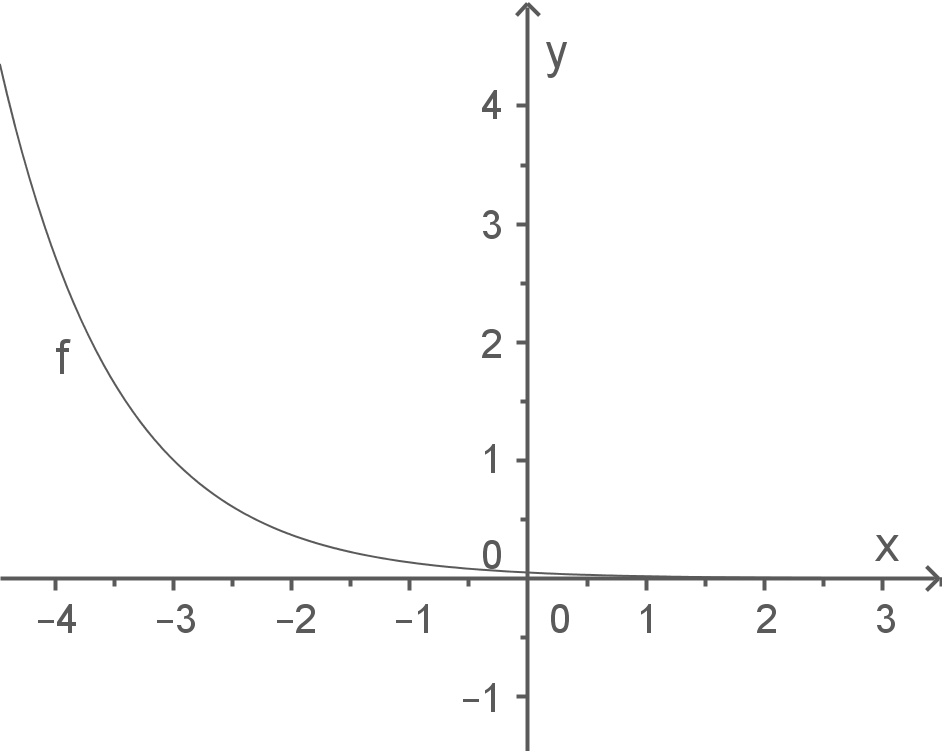
Das Schaubild von
f)
3.
a)
b)
c)
d)
e)
f)