a)
 Normalenform aufstellen
Normalenform aufstellen
Du sollst die Normalenform der Ebene

durch die drei Punkte

,

,

bestimmen. Die Normalenform erhältst du durch
Dabei bezeichnet

den Stützvektor, der der Ortsvektor eines beliebigen Punkts in der Ebene sein kann, und

einen Normalenvektor.
Der Normalenvektor kann beispielsweise durch das Kreuzprodukt zweier Vektoren gebildet werden, die in der Ebene liegen.
Dafür kannst du beispielsweise zwei Verbindungsvektoren der drei Punkte, die in der Ebene liegen sollen, verwenden:
Für eine Ebenengleichung kannst du auch das Vielfache des Normalenvektors verwenden. Du erhältst die Normalenform:
b)
 Lage der Ebene beschreiben
Lage der Ebene beschreiben
Du sollst die Lage der Ebene beschreiben, die die drei Punkte

,

und

enthält. Alle drei Punkte besitzen die gleiche

-Koordinate

.
Somit liegen die Punkte in einer Ebene, die zur

-Ebene parallel ist und zu ihr einen Abstand von

Längeneinheiten hat.
 Lage der Strecke nachweisen
Lage der Strecke nachweisen
Du sollst nachweisen, dass die Strecke
![\(\left[CC‘\right]\)](https://mathjax.schullv.de/5e3ebbca92294ba95bf738b81061f220186c58886ed4a6dc491335c2941cd8cd?color=5a5a5a)
senkrecht zur Ebene liegt, in der die drei Punkte


und

liegen. Dies ist der Fall, wenn der Vektor

senkrecht zur Ebene ist. Dazu bestimmst du zuerst die Koordinaten von

.
1. Schritt: Koordinaten von  bestimmen
bestimmen

entsteht durch Spiegelung von

an

.
2. Schritt:  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
\overrightarrow{CC‘}&=& \overrightarrow{OC‘}-\overrightarrow{OC} \\[5pt]
&=& \pmatrix{3\\3\\0}-\pmatrix{3\\3\\6} \\[5pt]
&=& \pmatrix{0\\0\\-6}
\end{array}\)](https://mathjax.schullv.de/d38834afba083351534d67129ff3267ab5795f0abbd3f55bfcdf037ae0ccc926?color=5a5a5a) 3. Schritt: Senkrechte nachweisen
3. Schritt: Senkrechte nachweisen
Vektoren welche senkrecht zu einer Ebene stehen sind Normalenvektoren. Da die Ebene parallel zur

-Ebene ist, ist ein möglicher Normalenvektor

Es gilt folgende Gleichung:
![\(\begin{array}[t]{rll}
\pmatrix{0\\0\\-6}&=& -6\cdot \pmatrix{0\\0\\1} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/1236fb5d6fb84012eb19cb447fca9193880590e174595be7ba016d8d714407ec?color=5a5a5a)
Der Verbindungsvektor

ist ein Vielfaches eines Normalenvektors der Ebene mit den Punktesn


und

und damit auch selbst ein Normalenvektor dieser Ebene. Der Vektor

steht also senkrecht auf der betrachteten Ebene und damit gilt das gleiche für die Strecke
![\([CC‘].\)](https://mathjax.schullv.de/3540b8ccba9b522f9777b060943ed7c0a99fac1acba2dc63b477237033174e09?color=5a5a5a)
c)
 Seitenlänge des Quadrats begründen
Seitenlänge des Quadrats begründen
Du sollst begründen, dass es sich bei dem Viereck

um ein Quadrat mit Seitenlänge

handelt. Bestimme zuerst die Koordinaten von

und

.
1. Schritt: Koordinaten von  und
und  bestimmen
bestimmen
Die Koordinaten von

und

bestimmst du wie die von

.
2. Schritt: Streckenlängen bestimmen
Du bestimmst die Streckenlängen über die Beträge der jeweiligen Verbindungsvektoren.
Für die zugehörigen Verbindungsvektoren folgt:
![\(\begin{array}[t]{rll}
\left|\overrightarrow{BA‘}\right|&=& \left|\pmatrix{-3 \\-3 \\0 }\right| \\[5pt]
&=& 3\sqrt{2}
\end{array}\)](https://mathjax.schullv.de/4ac21307402b489f0478bd431c2f5ebbcc54cbde368d12e68061313d5394ae2c?color=5a5a5a)
![\(\begin{array}[t]{rll}
\left|\overrightarrow{A‘B‘}\right|&=& \left|\pmatrix{3 \\-3 \\ 0}\right| \\[5pt]
&=& 3\sqrt{2}\\[10pt]
\end{array}\)](https://mathjax.schullv.de/2296d508aa07cee7f850c0eafec70e1930f7380201503e3613a8742a5995b552?color=5a5a5a)
![\(\begin{array}[t]{rll}
\left|\overrightarrow{B‘A}\right|&=& \left|\pmatrix{3 \\ 3\\ 0}\right| \\[5pt]
&=& 3\sqrt{2}
\end{array}\)](https://mathjax.schullv.de/b346782cf82182c05bafe02da67806a43d763de4f33bad289eeb96a807d481d3?color=5a5a5a)
Die Vektoren und damit auch die zugehörigen Strecken sind alle gleich lang. Um zu zeigen, dass es sich um ein Quadrat handelt und nicht um eine Raute ist ein rechter Winkel nachzuweisen.
3. Schritt: Rechter Winkel nachweisen
Für zwei rechtwinklige Vektoren gilt:
Betrachte die Vektoren ausgehend von Punkt

.
Ein Viereck mit vier gleich langen Seiten und einem rechten Winkel ist ein Quadrat, in diesem Fall mit der Seitenlänge

.
d)
 Volumen berechnen
Volumen berechnen
Du sollst das gegebene Volumen des Oktaeders nachweisen, das aus zwei Pyramiden mit quadratischer Grundfläche besteht. Für das Volumen einer Pyramide gilt

wobei

den Flächeninhalt der Grundfläche und

die Höhe der Pyramide bezeichnet.
Die Seitenlänge der quadratischen Grundfläche ist laut Aufgabenteil c)

Da

in der selben Ebene liegt und wegen Teilaufgabe b) ist die Höhe der Pyramide die Hälfte der Streckenlänge von
![\([CC‘]:\)](https://mathjax.schullv.de/ae53d5239e9de0d9f18e0f787690b05adea7e22ce34c9cc9819f05a058ccd6e8?color=5a5a5a)
![\(\begin{array}[t]{rll}
h&=& \frac{1}{2}\cdot \left| \overrightarrow{CC‘}\right| \\[5pt]
&=& \frac{1}{2}\cdot \left| \pmatrix{0\\0\\-6}\right| \\[5pt]
&=& 3
\end{array}\)](https://mathjax.schullv.de/5f6c6542269e14e0c709e96bbcd28f8fe1026121e68d2c8045736599ffb8f50d?color=5a5a5a)
Das Gesamtvolumen ergibt sich dann mit der obigen Formel:
![\(\begin{array}[t]{rll}
V&=& 2\cdot \frac{1}{3}\cdot \left(3\sqrt{2}\right)^2\cdot 3 \\[5pt]
&=& 2\cdot 18 \\[5pt]
&=& 36
\end{array}\)](https://mathjax.schullv.de/afb23bd42d701e30a121ef6fa120a419359596bec2639744c93beb69c177b58c?color=5a5a5a)
Wie gefordert berträgt das Volumen des Oktaeders

.
e)
 Winkel berechnen
Winkel berechnen
Du sollst die Größe des Winkels zwischen den Seitenflächen

und

bestimmen.
Dieser kann als Nebenwinkel des Schnittwinkels der beiden Ebenen betrachtet werden, in denen die beiden Dreiecke liegen. Einen Normalenvektor der Ebene

in der das Dreieck

liegt, hast du bereits bestimmt. Berechne einen Normalenvektor der Ebene, in der

liegt wie oben über das Kreuzprodukt zweier Verbindungsvektoren der Punkte in der Ebene:
Mit der Formel für den Schnittwinkel

zweier Ebenen folgt dann:
Für die Vektoren der Aufgabenstellung ergibt sich:
Der Winkel zwischen den beiden Seitenflächen

und

ist ca.

groß.
f)
 Kugelgleichung angeben
Kugelgleichung angeben
Du sollst eine Gleichung für die Kugel angeben, auf welcher alle Eckpunkte des Oktaeders liegen. Der Mittelpunkt dieser Kugel liegt in

, da die Punkte

,

,

und

alle den gleichen Abstand zu diesem haben. Der Radius ergibt sich somit beispielsweise aus der Länge des Vektors

.
![\(\begin{array}[t]{rll}
\left| \overrightarrow{AZ}\right|&=& \left|\pmatrix{3\\3\\3}-\pmatrix{6\\3\\3}\right| \\[5pt]
&=& \left|\pmatrix{-3\\0\\0}\right| \\[5pt]
&=& 3
\end{array}\)](https://mathjax.schullv.de/902d11356f659221f30af968bd4269477782ae6ad2586cf396ad60d752ec4c3e?color=5a5a5a)
Der Radius beträgt

somit ergibt sich die Kugelgleichung:
 Volumen der Kugel und des Oktaeders vergleichen
Volumen der Kugel und des Oktaeders vergleichen
Du sollst die Volumina der Kugel und des Oktaeders vergleichen. Das Volumen des Oktaeders beträgt

. Für das Kugelvolumen gilt:
Für

gilt:
![\(\begin{array}[t]{rll}
V&=& \frac{4}{3}\cdot\pi\cdot 3^3 \\[5pt]
&=& 36\pi
\end{array}\)](https://mathjax.schullv.de/d309380d0595e56599f07c4f578927d2db2ae0097c391447673c83c2c6ba2982?color=5a5a5a)
Für den Anteil des Oktaedervolumens am Volumen der Kugel folgt daher:
Das Oktaedervolumen nimmt ca.

des Kugelvolumens ein.
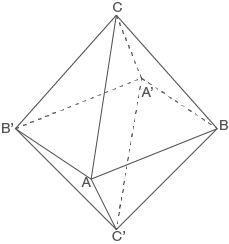
 ,
,  und
und  das gleichseitige Dreieck
das gleichseitige Dreieck  fest.
fest.
 und
und  am Symmetriezentrum
am Symmetriezentrum  , so erhält man die Punkte
, so erhält man die Punkte  und
und  .
.
 , in der das Dreieck
, in der das Dreieck  liegt, in Normalenform.
(mögliches Ergebnis:
liegt, in Normalenform.
(mögliches Ergebnis:  )
)
 und
und  liegen, im Koordinatensystem. Zeige, dass die Strecke
liegen, im Koordinatensystem. Zeige, dass die Strecke ![\([CC‘]\)](https://mathjax.schullv.de/fa164b6e9cc4fb3d981051d34a653352a5075c84d0f23d6834e49c9b7f2396bb?color=5a5a5a) senkrecht auf dieser Ebene steht.
senkrecht auf dieser Ebene steht.
 ein Quadrat mit der Seitenlänge
ein Quadrat mit der Seitenlänge  ist.
ist.
 ist ein sogenanntes Oktaeder. Er besteht aus zwei Pyramiden mit dem Quadrat
ist ein sogenanntes Oktaeder. Er besteht aus zwei Pyramiden mit dem Quadrat  als gemeinsamer Grundfläche und den Pyramidenspitzen
als gemeinsamer Grundfläche und den Pyramidenspitzen  bzw.
bzw.  .
.
 besitzt.
besitzt.
 und
und  .
.