Teil A
1
Gegeben ist die Funktion  mit
mit  und maximalem Definitionsbereich.
und maximalem Definitionsbereich.
a)
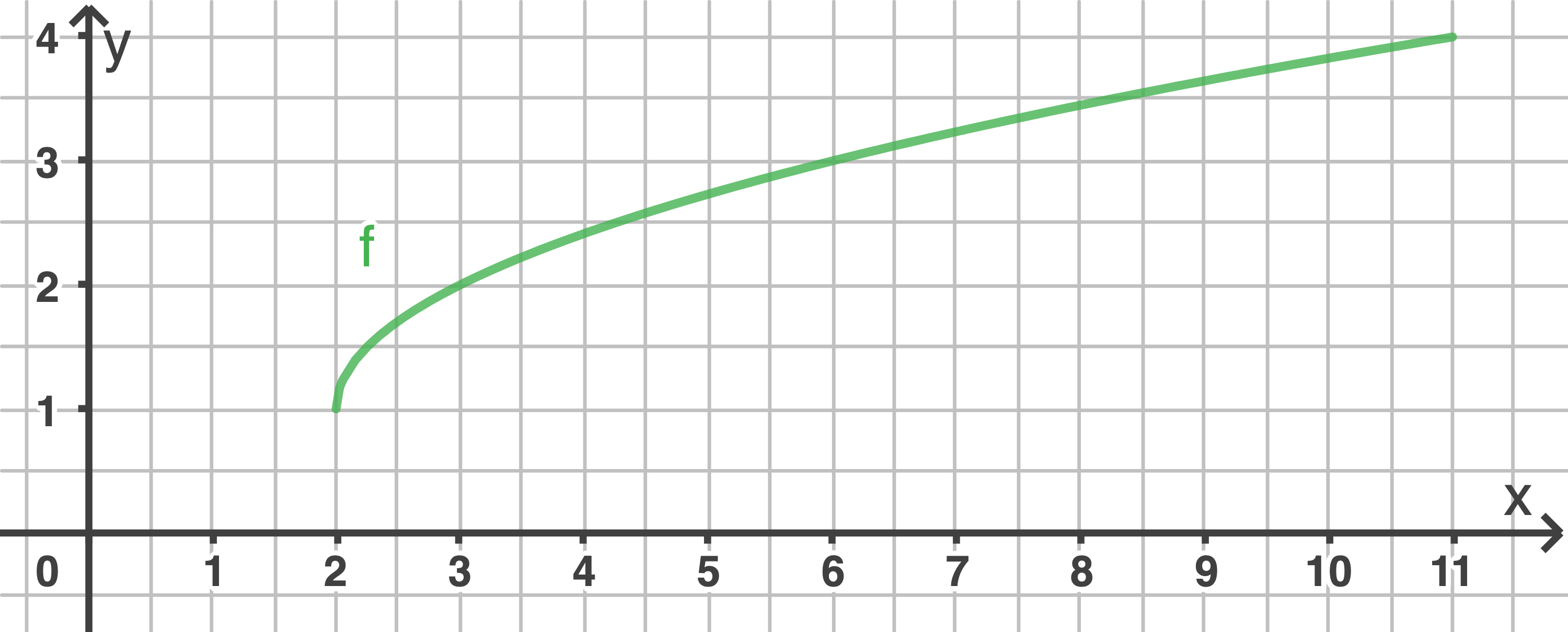
Zeichne den Graphen von  im Bereich
im Bereich  in ein Koordinatensystem.
in ein Koordinatensystem.
(3 BE)
b)
Berechne den Wert des Integrals 
(3 BE)
2
Gib jeweils den Term einer in  definierten Funktion an, die die angegebene Wertemenge
definierten Funktion an, die die angegebene Wertemenge  hat.
hat.
![\(W=\;]- \infty; 1]\)](https://mathjax.schullv.de/89eb27fa7411562ed21daef1ebbe1532fbd91f0d29761e61bfef9017830cd123?color=5a5a5a)
![\(W=\;]3;+\infty [\)](https://mathjax.schullv.de/e47201f599fd29d931b24f17dd2ffd6ee6ccddc04f4503f387a41342f1b9dc84?color=5a5a5a)
a)
(2 BE)
b)
(2 BE)
3
a)
Betrachtet werden eine in  definierte ganzrationale Funktion
definierte ganzrationale Funktion  und der Punkt
und der Punkt 
Beschreibe, wie man rechnerisch die Gleichung der Tangente an den Graphen von im Punkt
im Punkt  ermitteln kann.
ermitteln kann.
Beschreibe, wie man rechnerisch die Gleichung der Tangente an den Graphen von
(2 BE)
b)
Gegeben ist eine in  definierte Funktion
definierte Funktion  mit
mit  deren Graph im Punkt
deren Graph im Punkt  die Tangente mit der Gleichung
die Tangente mit der Gleichung  besitzt. Bestimme
besitzt. Bestimme  und
und 
(3 BE)
4
Die Abbildung zeigt den Graphen  einer in
einer in  definierten Funktion
definierten Funktion 
 ist streng monoton fallend und schneidet die x-Achse im Punkt
ist streng monoton fallend und schneidet die x-Achse im Punkt 
Betrachtet wird ferner die Funktion mit
mit  und maximalem Definitionsbereich
und maximalem Definitionsbereich 
Betrachtet wird ferner die Funktion
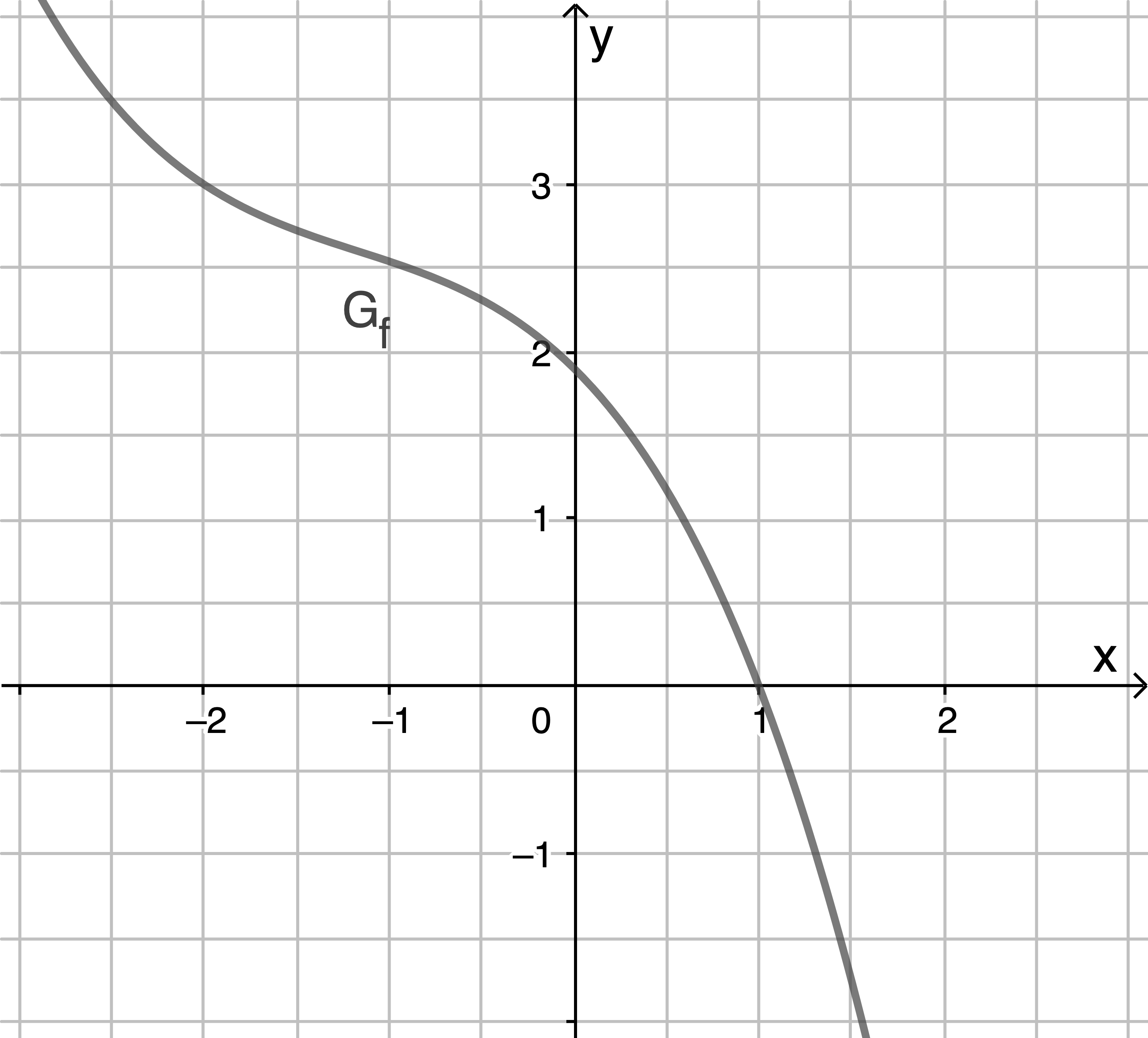
a)
Begründe, dass  nicht in
nicht in  enthalten ist, und gib den Funktionswert
enthalten ist, und gib den Funktionswert  an.
an.
(2 BE)
b)
Ermittle mithilfe der Abbildung die x-Koordinaten der Schnittpunkte der Graphen von  und
und 
(3 BE)
(20 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
2
a)
b)
3
a)
- Ableitung von
bilden und Einsetzen der
-Koordinate von
liefert die Steigung
der gesuchten Tangente
- Einsetzen von
und der Koordinaten von
in die Tangentengleichung
und nach
auflösen liefert den gesuchten Wert für
- Einsetzen von
und
in
ergibt die gesuchte Tangentengleichung
b)
Für die Ableitung von  gilt
gilt  Somit folgt:
Somit folgt:
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/c6fb4f6564727f80f20ff8d34da54be81345d461ce20b1bd8e2731fc72b63bb0?color=5a5a5a) Die Koordinaten von
Die Koordinaten von  eingesetzt in
eingesetzt in  ergeben weiter:
ergeben weiter:
![\(\begin{array}[t]{rll}
h(1) &=& 0\\[5pt]
-\dfrac{1}{2}\cdot 1 +c &=&0 &\quad \scriptsize \mid\;+\dfrac{1}{2} \\[5pt]
c&=&\dfrac{1}{2}
\end{array}\)](https://mathjax.schullv.de/52f5794fa8698419edf58f38dffc956bc9bd64e350db0f16bac5b584f8fdc03c?color=5a5a5a)
4
a)
Begründen, dass  nicht in
nicht in  ist
Da
ist
Da  gilt, kann
gilt, kann  nicht in
nicht in  enthalten sein, da sonst im Funktionsterm von
enthalten sein, da sonst im Funktionsterm von  an der Stelle
an der Stelle  durch Null dividiert werden würde.
Funktionswert
durch Null dividiert werden würde.
Funktionswert  angeben
Aus der Abbildung folgt
angeben
Aus der Abbildung folgt  und somit
und somit 
b)