Teil A
1
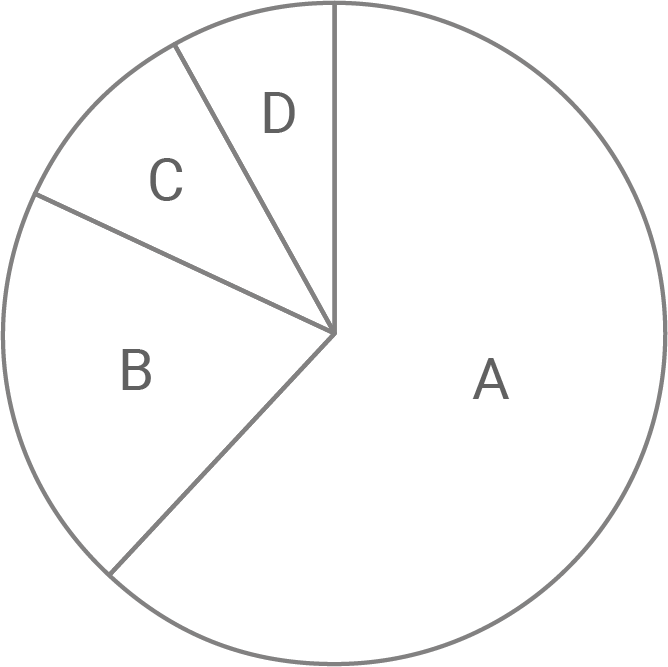
Anlässlich einer Studie wurden 300 weibliche und 700 männliche Bewohner einer Großstadt im Alter von 18 bis 30 Jahren dazu befragt, ob sie Interesse an Car-Sharing haben. 
der Befragten waren weiblich und gaben an, nicht interessiert zu sein. 
der Befragten waren männlich und gaben an, Interesse an Car-Sharing zu haben. Das Kreisdiagramm veranschaulicht die absoluten Häufigkeiten, die sich bei der Befragung ergaben.
1
Frauen mit Interesse an Car-Sharing
2
Frauen ohne Interesse an Car-Sharing
3
Männer mit Interesse an Car-Sharing
4
Männer ohne Interesse an Car-Sharing
a)
Ordne die Beschriftungen 1 bis 4 den Sektoren A bis D korrekt zu und begründe deine Zuordnung.
(4 BE)
b)
Berechne die Größe des Mittelpunktswinkels desjenigen Sektors, der den Anteil der Befragten veranschaulicht, die männlich waren und angaben, Interesse an Car-Sharing zu haben.
(1 BE)
2
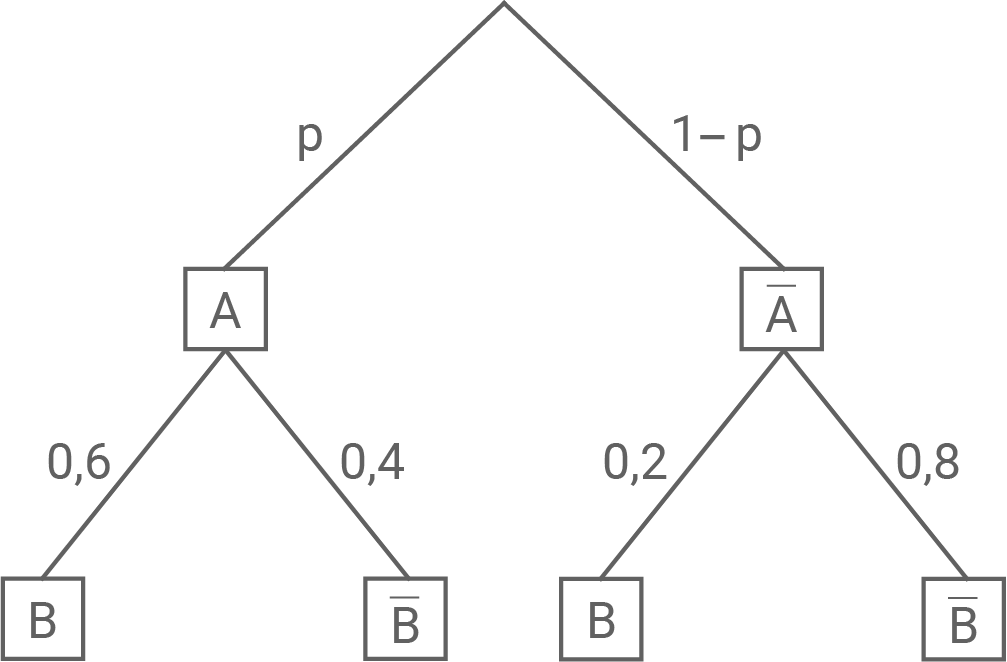
Das abgebildete Baumdiagramm stellt ein zweistufiges Zufallsexperiment mit den Ereignissen 
und 
sowie deren Gegenereignissen 
und 
dar.
a)
Bestimme den Wert von 
so, dass das Ereignis bei diesem Zufallsexperiment mit der Wahrscheinlichkeit 
eintritt.
(2 BE)
b)
Ermittle den größtmöglichen Wert, den die Wahrscheinlichkeit von annehmen kann.
(3 BE)
(10 BE)
1
a)
Für die Anzahl der Frauen ohne Interesse an Car-Sharing folgt:
Von den insgesamt 
Frauen haben somit 
Interesse an Car-Sharing. Für die Anzahl der männlich Befragten, die Interesse an Car-Sharing haben gilt:
Von den insgesamt 
männlichen Befragten haben damit 
kein Interesse an Car-Sharing.
Anhand der absoluten Zahlen folgt somit, dass Beschriftung 4 zum größten Sektor, das heißt Sektor 
gehört, Beschriftung 2 zum Sektor gehört, Beschriftung 1 zum Sektor 
gehört und Beschriftung 3 zum kleinsten Sektor, das heißt Sektor 
gehört.
b)
2
a)
Mit den Pfadregeln folgt für die gesuchte Wahrscheinlichkeit:
b)
Mit Hilfe von Aufgabenteil a) folgt für die Wahrscheinlichkeit von in Abhängigkeit von folgende Funktion:
Diese Funktion beschreibt eine Gerade mit positiver Steigung. Die Wahrscheinlichkeit von ist somit für den maximalen Wert von am größten, das heißt für 
Damit ist 
der größtmögliche Wert, den die Wahrscheinlichkeit von annehmen kann.