Teil B

Eine Geothermieanlage fördert durch einen Bohrkanal heißes Wasser aus einer wasserführenden Gesteinsschicht an die Erdoberfläche. In einem Modell entspricht die $x_1 x_2$ -Ebene eines kartesischen Koordinatensystems der horizontal verlaufenden Erdoberfläche. Eine Längeneinheit im Koordinatensystem entspricht einem Kilometer in der Realität. Der Bohrkanal besteht aus zwei Abschnitten, die im Modell vereinfacht durch die Strecken $[A P]$ und $[P Q]$ mit den Punkten $A(0\mid0\mid 0),$ $P(0\mid0\mid-1)$ und $Q(1\mid1\mid-3,5)$ beschrieben werden (vgl. Abbildung).

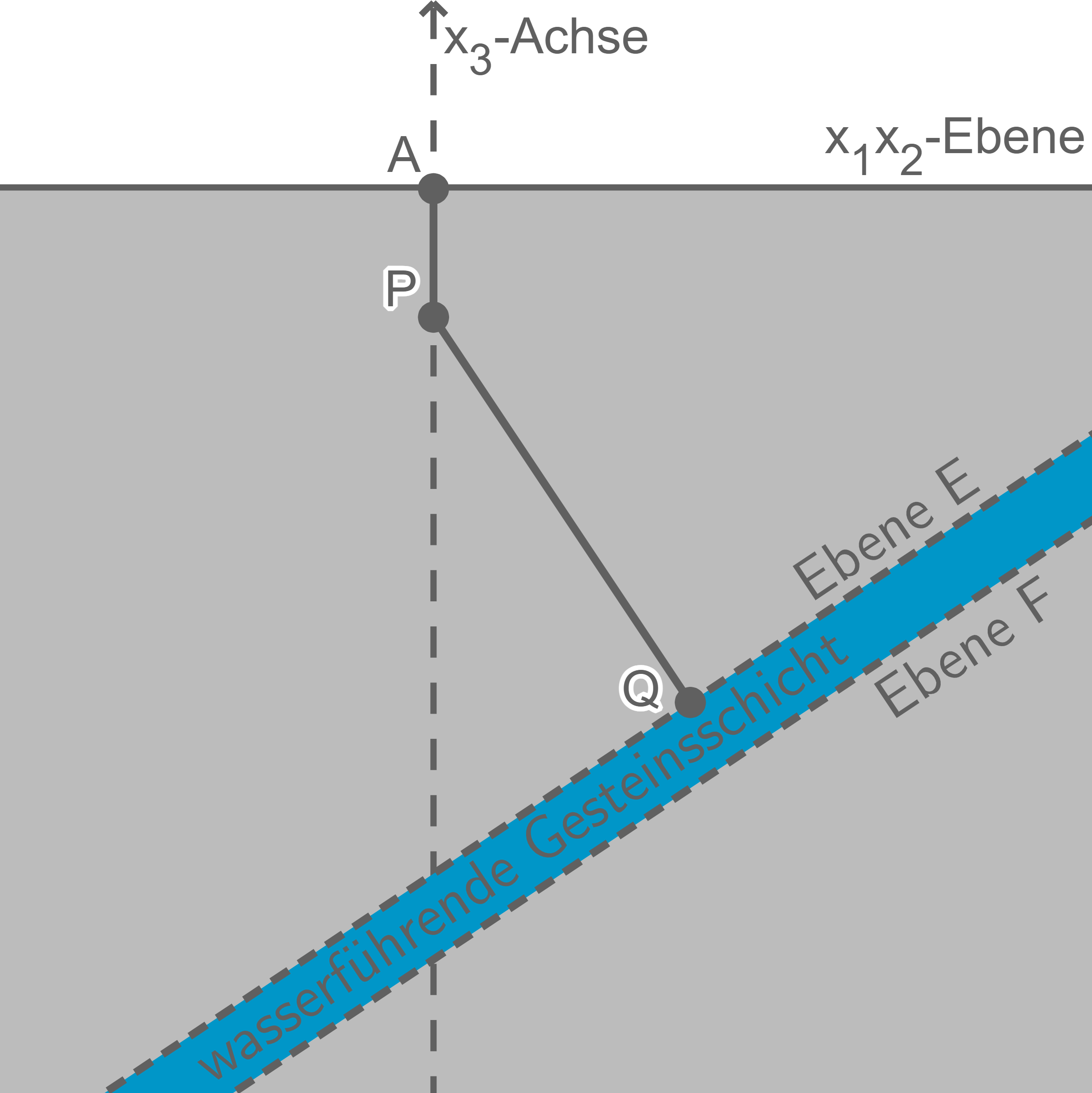
Schematische Skizze (nicht maßstabsgetreu)

Berechne auf der Grundlage des Modells die Gesamtlänge des Bohrkanals auf Meter gerundet.

(2 BE)

Beim Übergang zwischen den beiden Abschnitten des Bohrkanals muss die Bohrrichtung um den Winkel geändert werden, der im Modell durch den Schnittwinkel der beiden Geraden $AP$ und $PQ$ beschrieben wird. Bestimme die Größe dieses Winkels.

(3 BE)

Im Modell liegt die obere Begrenzungsfläche der wasserführenden Gesteinsschicht in der Ebene $E$ und die untere Begrenzungsfläche in einer zu $E$ parallelen Ebene $F.$ Die Ebene $E$ enthält den Punkt $Q.$ Die Strecke $[PQ]$ steht senkrecht auf der Ebene $E$ (vgl. Abbildung).

Bestimme eine Gleichung der Ebene $E$ in Normalenform.

(zur Kontrolle: $E: 4x_1+4x_2-10x_3-43=0$ )

(2 BE)

Der Bohrkanal wird geradlinig verlängert und verlässt die wasserführende Gesteinsschicht in einer Tiefe von $3600\;\text{m}$ unter der Erdoberfläche. Die Austrittsstelle wird im Modell als Punkt $R$ auf der Geraden $PQ$ beschrieben. Bestimme die Koordinaten von $R$ und ermittle die Dicke der wasserführenden Gesteinsschicht auf Meter gerundet.

(zur Kontrolle: $x_1$ - und $x_2$ -Koordinate von $R: 1,04$ )

(6 BE)

Ein zweiter Bohrkanal wird benötigt, durch den das entnommene Wasser abgekühlt zurück in die wasserführende Gesteinsschicht geleitet wird. Der Bohrkanal soll geradlinig und senkrecht zur Erdoberfläche verlaufen. Für den Beginn des Bohrkanals an der Erdoberfläche kommen nur Bohrstellen in Betracht, die im Modell durch einen Punkt $B(t\mid-t\mid 0)$ mit $t \in \mathbb{R}$ beschrieben werden können.

Zeige rechnerisch, dass der zweite Bohrkanal die wasserführende Gesteinsschicht im Modell im Punkt $T (t\mid-t\mid-4,3)$ erreicht, und erläutere, wie die Länge des zweiten Bohrkanals bis zur wasserführenden Gesteinsschicht von der Lage der zugehörigen Bohrstelle beeinflusst wird.

(3 BE)

Aus energetischen Gründen soll der Abstand der beiden Stellen, an denen die beiden Bohrkanäle auf die wasserführende Gesteinsschicht treffen, mindestens $1500\;\text{m}$ betragen. Entscheide auf der Grundlage des Modells, ob diese Bedingung für jeden möglichen zweiten Bohrkanal erfüllt wird.

(4 BE)

(20 BE)

Rechenweg anzeigen

$3,872\,\text{km}$

Insgesamt ist der Bohrkanal ungefähr $3,872\,\text{km}$ und somit ca. $3.872\,\text{m}$ lang.

$\begin{array}[t]{rll} \cos(\alpha) &=& \dfrac{\left|\overrightarrow{AP}\circ \overrightarrow{PQ} \right| }{\left|\overrightarrow{AP} \right| \cdot \left| \overrightarrow{PQ} \right| } \\[5pt] \cos(\alpha)&=& \dfrac{\left|\pmatrix{0\\0\\-1}\circ \pmatrix{1\\1\\-2,5}\right| }{\left|\pmatrix{0\\0\\-1} \right| \cdot \left| \pmatrix{1\\1\\-2,5} \right| } \\[5pt] \cos(\alpha)&=& \dfrac{2,5 }{1 \cdot \sqrt{8,25} } \\[5pt] \cos(\alpha)&=& \dfrac{2,5 }{ \sqrt{8,25} }\\[5pt] \alpha &\approx& 29,5^{\circ} \end{array}$

Da die Strecke $[PQ]$ senkrecht auf der Ebene $E$ steht, kann der Vektor $\overrightarrow{PQ}$ als Normalenvektor verwendet werden, somit folgt:

$E:x_1 +x_2 -2,5x_3 = d$

Einsetzen der Koordinaten von $Q$ liefert für $d:$

$\begin{array}[t]{rll} 1\cdot 1 +1\cdot 1 -2,5 \cdot (-3,5) &=& d \\[5pt] 10,75&=& d \end{array}$

Eine Gleichung von $E$ in Normalenform lautet somit:

Rechenweg anzeigen

$E:4x_1+4x_2-10x_3-43=0$

Koordinaten bestimmen

Der Punkt $R$ liegt auf der Geraden $PQ$ und besitzt die $x_3$ -Koordinate $-3,6.$ Für die Gerade $PQ$ ergibt sich zum Beispiel die folgende Geradengleichung:

$\begin{array}[t]{rll} PQ:\overrightarrow{x} &=& \overrightarrow{OP} + r\cdot \overrightarrow{PQ} \\[5pt] &=& \pmatrix{0\\0\\-1} + r\cdot \pmatrix{1\\1\\-2,5} \end{array}$

Einsetzen der allgemeinen Form des Stützvektors von $R$ in die Geradengleichung liefert:

Rechenweg anzeigen

$\pmatrix{x_1\\x_2 \\ -2,6} = r\cdot \pmatrix{1\\1\\-2,5}$

Aus der dritten Zeile folgt:

$\begin{array}[t]{rll} -2,6 &=& -2,5r &\quad \scriptsize \mid\; :(-2,5) \\[5pt] 1,04 &=& r \end{array}$

Nach der ersten und zweiten Zeile gilt somit $x_1=x_2 = 1,04.$ Der Punkt $R,$ der im Modell die Austrittsstelle beschreibt, besitzt damit die Koordinaten $R(1,04\mid 1,04\mid -3,6).$

Dicke der wasserführenden Gesteinsschicht ermitteln

Die Dicke der wasserführenden Gesteinsschicht wird im Modell durch den Abstand der beiden Punkte $Q$ und $R$ beschrieben. Somit folgt:

Rechenweg anzeigen

$\left|\overrightarrow{QR} \right| \approx 0,115\,\text{km}$

Die wasserführende Gesteinsschicht ist ungefähr $0,115\,\text{km}$ und damit ca. $115\,\text{m}$ dick.

Punkt rechnerisch zeigen

Der zweite Bohrkanal durch die Gerade $h$ mit der folgenden Geradengleichung beschrieben werden:

$\begin{array}[t]{rll} h: \overrightarrow{x} &=& \overrightarrow{OB} + s\cdot \pmatrix{0\\0\\1} \\[5pt] &=& \pmatrix{t\\-t\\0} + s\cdot \pmatrix{0\\0\\1} \\[5pt] &=& \pmatrix{t\\-t\\s} \end{array}$

Die Ebene $E$ beschreibt die obere Begrenzung der wasserführenden Gesteinsschicht. Der Punkt $T$ ist somit der Punkt, in dem die Gerade $h$ auf die Ebene $E$ trifft.
Einsetzen der allgemeinen Koordinaten eines Punktes der Geraden $h$ in die Ebenegleichung von $E$ liefert:

Rechenweg anzeigen

$s = -4,3$

Der zweite Bohrkanal erreicht die wasserführende Gesteinsschicht im Modell somit im Punkt mit den Koordinaten $T(t\mid -t \mid -4,3).$

Beeinflussung der Länge des Kanals erläutern

Da der Punkt $B$ für alle Werte von $t$ senkrecht über $T$ liegt, ist die Länge des zweiten Bohrkanals unabhängig von der Lage von $B$ und beträgt immer $4,3\,\text{km}=4300\,\text{m}.$

Rechenweg anzeigen

$t^2 \geq -0,195$

Da stets $t^2 \geq 0$ gilt, ist diese Ungleichung für alle Werte $t\in \mathbb{R}$ erfüllt. Somit ist der geforderte Mindestabstand für jeden möglichen zweiten Bohrkanal erfüllt.