Teil A
1
Gegeben ist die Funktion  mit maximalem Definitionsbereich
mit maximalem Definitionsbereich 
a)
Bestimme  und gib die Koordinaten des Schnittpunkts des Graphen von
und gib die Koordinaten des Schnittpunkts des Graphen von  mit der
mit der  -Achse an.
-Achse an.
(3 BE)
b)
Gib einen Term der ersten Ableitungsfunktion von  an.
an.
(2 BE)
2
Gegeben ist die in  definierte Funktion
definierte Funktion 
a)
Bestimme eine Gleichung der Tangente an den Graphen von  im Punkt
im Punkt 
(3 BE)
b)
Die Funktion  ist umkehrbar. Die Umkehrfunktion
ist umkehrbar. Die Umkehrfunktion  von
von  ist in
ist in  definiert. Bestimme einen Term von
definiert. Bestimme einen Term von  .
.
(2 BE)
3
Gegeben ist die in  definierte Funktion
definierte Funktion  und
und ![\(a \in\left] 1 ;+\infty \right[.\)](https://mathjax.schullv.de/ded95900b400683b295fb2c95383949c96a33065af11d4611c5feb0ff47ee544?color=5a5a5a) Die Nullstellen von
Die Nullstellen von  sind
sind  und
und 
a)
Zeige, dass das Flächenstück, das der Graph von  mit der
mit der  -Achse einschließt, den Inhalt
-Achse einschließt, den Inhalt  hat.
hat.
(2 BE)
b)
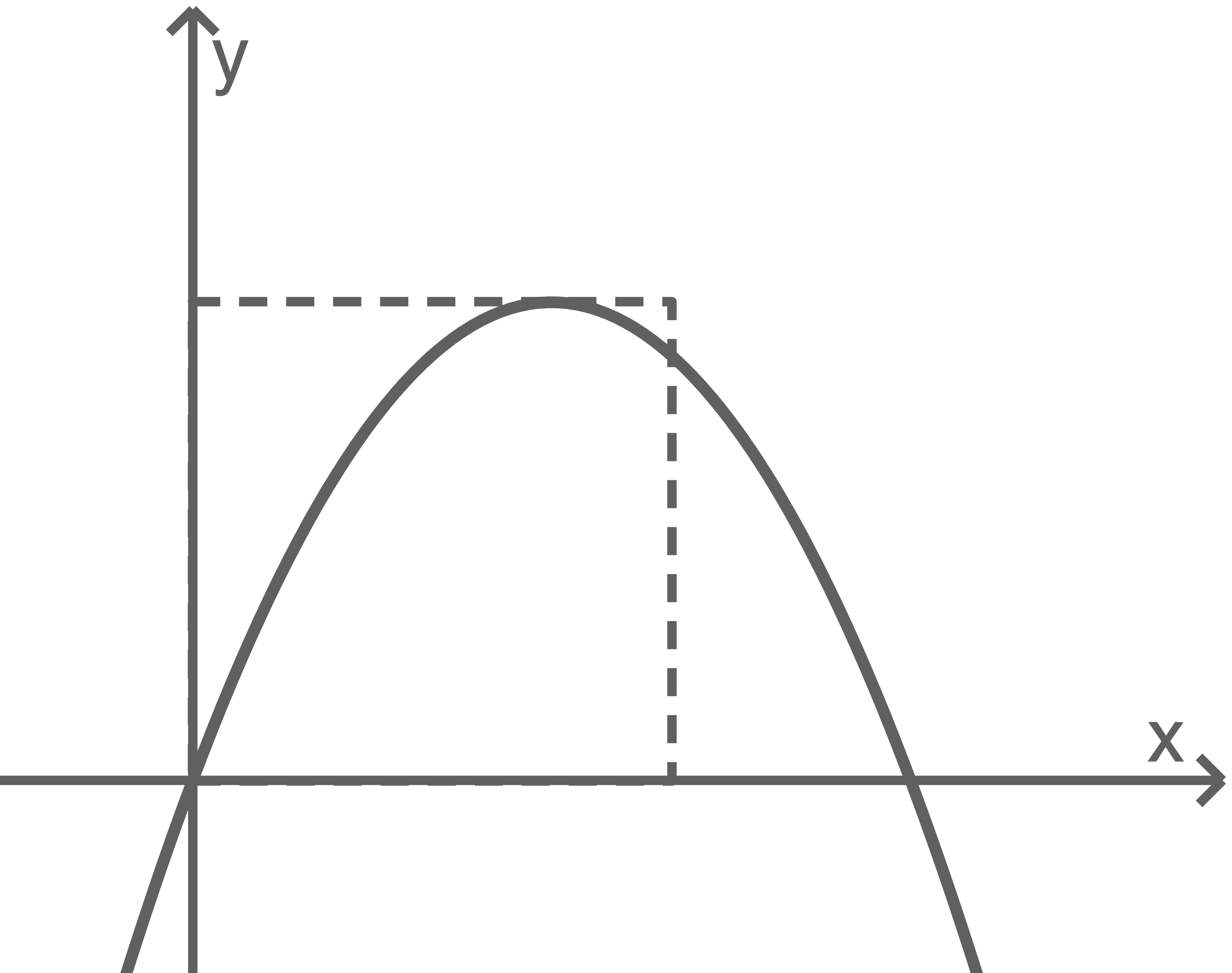
Der Hochpunkt des Graphen von  liegt auf einer Seite eines Quadrats; zwei Seiten dieses Quadrats liegen auf den Koordinatenachsen (vgl. Abbildung 1). Der Flächeninhalt des Quadrats stimmt mit dem Inhalt des Flächenstücks, das der Graph von
liegt auf einer Seite eines Quadrats; zwei Seiten dieses Quadrats liegen auf den Koordinatenachsen (vgl. Abbildung 1). Der Flächeninhalt des Quadrats stimmt mit dem Inhalt des Flächenstücks, das der Graph von  mit der
mit der  -Achse einschließt, überein. Bestimme den Wert von
-Achse einschließt, überein. Bestimme den Wert von 

Abb. 1
(3 BE)
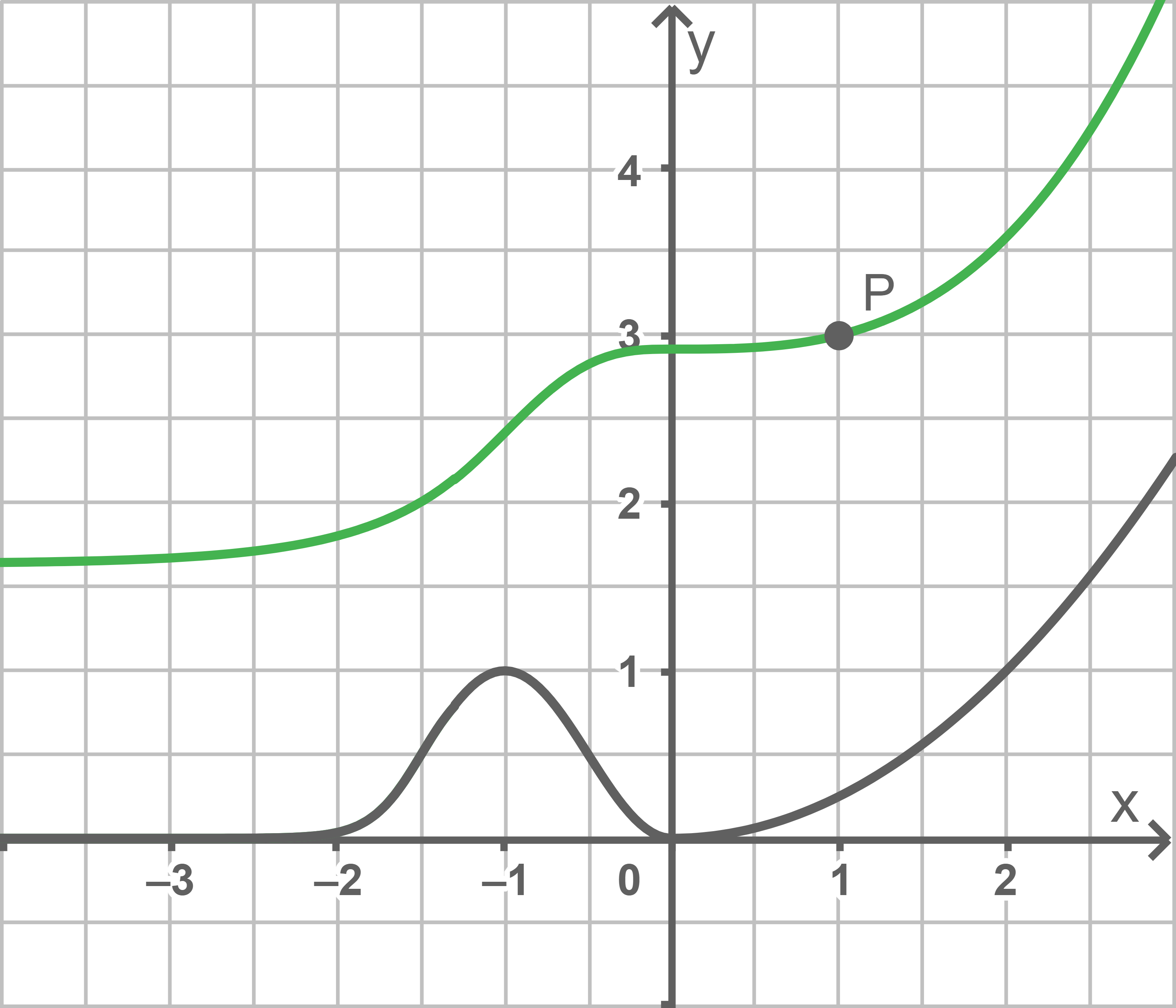
4
Abbildung 2 zeigt den Graphen der in  definierten Funktion
definierten Funktion  dessen einzige Extrempunkte
dessen einzige Extrempunkte  und
und  sind, sowie den Punkt
sind, sowie den Punkt 
Abb. 2
a)
Gib die Koordinaten des Tiefpunkts des Graphen der in  definierten Funktion
definierten Funktion  mit
mit  an.
an.
(2 BE)
b)
Der Graph einer Stammfunktion von  verläuft durch
verläuft durch  Skizziere diesen Graphen in Abbildung 2.
Skizziere diesen Graphen in Abbildung 2.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Definitionsmenge  bestimmen
Da für
bestimmen
Da für  der Nenner von
der Nenner von  Null wird, folgt für den maximalen Definitionsbereich von
Null wird, folgt für den maximalen Definitionsbereich von  somit
somit  Koordinaten des Schnittpunktes mit der
Koordinaten des Schnittpunktes mit der  -Achse angeben
-Achse angeben



 Der Schnittpunkt des Graphen von
Der Schnittpunkt des Graphen von  mit der
mit der  -Achse hat somit die Koordinaten
-Achse hat somit die Koordinaten 
b)
Mit der Quotientenregel folgt:



2
a)
Für die Steigung der Tangente  mit
mit  gilt:
gilt:
 Mit
Mit  folgt:
folgt:
 Zudem gilt:
Zudem gilt:
 Einsetzen in die Tangentengleichung:
Einsetzen in die Tangentengleichung:
![\(\begin{array}[t]{rll}
y &=& \dfrac{1}{2}\cdot x + b &\quad \scriptsize \mid\; (1\mid 2) \\[5pt]
2&=& \dfrac{1}{2}\cdot 1 +b &\quad \scriptsize \mid\; -\dfrac{1}{2}\\[5pt]
\dfrac{3}{2}&=& b
\end{array}\)](https://mathjax.schullv.de/0a68a9c6156c10cc83688a0e5a82478b292316bb0d91b192070feb1d2dcb45b3?color=5a5a5a) Eine Gleichung der Tangente ist somit durch
Eine Gleichung der Tangente ist somit durch  gegeben.
gegeben.
b)
3
a)
b)
1. Schritt: Koordinaten des Hochpunkts bestimmen
 Notwendige Bedingung:
Notwendige Bedingung:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/30ebf3c76e2257be5d2a68c9d5613d850fd163fd0eefa5c35445226e86e99bbe?color=5a5a5a) Auf das Überprüfen der hinreichenden Bedingung kann verzichtet werden, da es sich laut Aufgabenstellung bei dem Extremum um einen Hochpunkt handelt.
Auf das Überprüfen der hinreichenden Bedingung kann verzichtet werden, da es sich laut Aufgabenstellung bei dem Extremum um einen Hochpunkt handelt.
 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
f(a)&=&-a^2 + 2a \cdot a \\[5pt]
&=& -a^2 + 2 a^2 \\[5pt]
&=& a^2
\end{array}\)](https://mathjax.schullv.de/eee637f16178de32501be8d5ccf41686d517db7a1581069456d8a935557d3db0?color=5a5a5a) Der Hochpunkt des Graphen von
Der Hochpunkt des Graphen von  hat somit die Koordinaten
hat somit die Koordinaten  2. Schritt: Flächinhalt berechnen
Da der Hochpunkt des Graphen von
2. Schritt: Flächinhalt berechnen
Da der Hochpunkt des Graphen von  auf der oberen Seite des Quadrats liegt, muss die Seitenlänge des Quadrats
auf der oberen Seite des Quadrats liegt, muss die Seitenlänge des Quadrats  betragen. Der Flächeninhalt des Quadrats ist somit
betragen. Der Flächeninhalt des Quadrats ist somit ![\(a^2 \cdot a^2 = a^4 \; [\text{FE}].\)](https://mathjax.schullv.de/44032a918304531969c6d5e030a4ccee59ddc65074c7de06ac7082dd53aa7b3a?color=5a5a5a) 3. Schritt:
3. Schritt:  bestimmen
Gleichsetzen und nach
bestimmen
Gleichsetzen und nach  auflösen liefert:
auflösen liefert:
![\(\begin{array}[t]{rll}
a^4&=& \dfrac{4}{3}a^3&\quad \scriptsize \mid\; -\dfrac{4}{3}a^3 \\[5pt]
a^4 -\dfrac{4}{3}a^3 &=& 0 \\[5pt]
a^3\left(a- \dfrac{4}{3}\right) &=& 0 \\[5pt]
a_1 &=& 0 \\[5pt]
a_2 &=& \dfrac{4}{3}
\end{array}\)](https://mathjax.schullv.de/751a50b1ada8633624d74eb6047e5a8e53bd0ae012b6fda570baff60329ada09?color=5a5a5a) Da
Da ![\(a \in \left]1; + \infty \right[\)](https://mathjax.schullv.de/79694e596309e828f2023b1d1ace70c0fcaafd327c35db7c24241f23b9098ccf?color=5a5a5a) , gilt
, gilt 
4
a)
Der Graph von  enspricht dem an der
enspricht dem an der  -Achse gespiegelten und um
-Achse gespiegelten und um  Längeneinheiten in
Längeneinheiten in  -Richtung verschobenen Graphen von
-Richtung verschobenen Graphen von 
Durch die Spiegelung an der -Achse verändert sich der Hochpunkt des Graphen von
-Achse verändert sich der Hochpunkt des Graphen von  zu einem Tiefpunkt mit der
zu einem Tiefpunkt mit der  -Koordinate
-Koordinate 
Durch die anschließende Verschiebung ändert sich die -Koordinate des Tiefpunkts zu
-Koordinate des Tiefpunkts zu  Der Tiefpunkt hat also die Koordinaten
Der Tiefpunkt hat also die Koordinaten 
Durch die Spiegelung an der
Durch die anschließende Verschiebung ändert sich die
b)