Teil B
Gegeben ist die in ![\([0;10]\)](https://mathjax.schullv.de/d8eeb4818039bb69f6a7765f496e726747007838c92f84f8227eeb9ef0f7e11f?color=5a5a5a) definierte Funktion
definierte Funktion  Der Graph von
Der Graph von  wird mit
wird mit  bezeichnet.
bezeichnet.
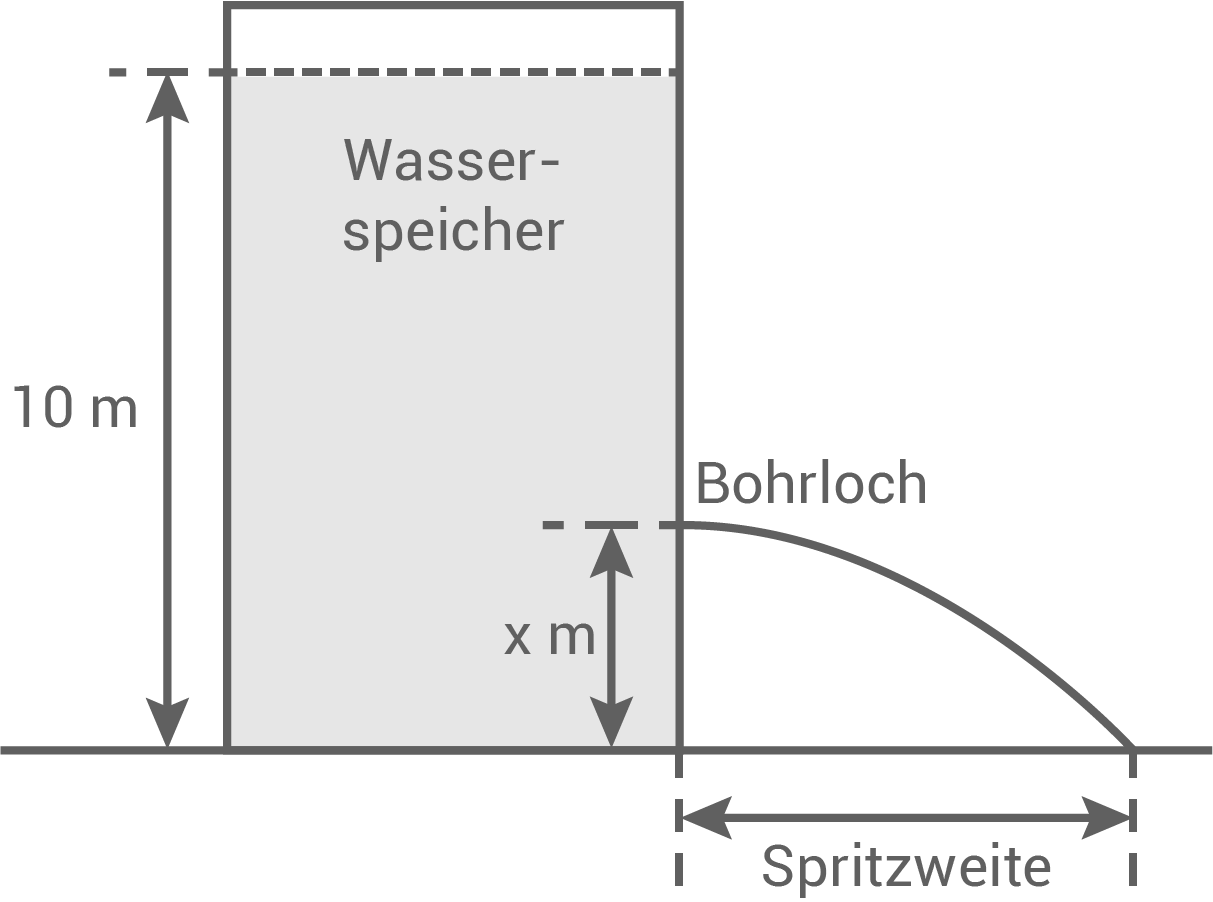 Diese Entfernung wird im Folgenden Spritzweite genannt (vgl. Abbildung). Die Abhängigkeit der Spritzweite von der Höhe des Bohrlochs wird durch die in den bisherigen Teilaufgaben betrachtete Funktion
Diese Entfernung wird im Folgenden Spritzweite genannt (vgl. Abbildung). Die Abhängigkeit der Spritzweite von der Höhe des Bohrlochs wird durch die in den bisherigen Teilaufgaben betrachtete Funktion  modellhaft beschrieben. Dabei ist
modellhaft beschrieben. Dabei ist  die Höhe des Bohrlochs über dem Speicherboden in Metern und
die Höhe des Bohrlochs über dem Speicherboden in Metern und  die Spritzweite in Metern.
die Spritzweite in Metern.
a)
Bestimme die Nullstellen von  .
[Zur Kontrolle:
.
[Zur Kontrolle:  und
und  ]
]
(2 BE)
b)
Der Graph  besitzt in genau einem Punkt eine waagrechte Tangente.
besitzt in genau einem Punkt eine waagrechte Tangente.
Bestimme die Koordinaten dieses Punkts und begründe, dass es sich um einen Hochpunkt handelt. [Zur Kontrolle:
 -Koordinate des Hochpunkts:
-Koordinate des Hochpunkts:  ]
]
Bestimme die Koordinaten dieses Punkts und begründe, dass es sich um einen Hochpunkt handelt. [Zur Kontrolle:
(5 BE)
c)
Der Graph  ist rechtsgekrümmt. Einer der folgenden Terme ist ein Term der zweiten Ableitungsfunktion
ist rechtsgekrümmt. Einer der folgenden Terme ist ein Term der zweiten Ableitungsfunktion  von
von  Beurteile, ob dies Term I oder Term II ist, ohne einen Term von
Beurteile, ob dies Term I oder Term II ist, ohne einen Term von  zu berechnen.
zu berechnen.


I
II
(3 BE)
d)
Weise nach, dass für  die Gleichung
die Gleichung  erfüllt ist, indem du die Terme
erfüllt ist, indem du die Terme  und
und  geeignet umformst.
geeignet umformst.
Begründe damit, dass der Graph symmetrisch bezüglich der Gerade mit der Gleichung
symmetrisch bezüglich der Gerade mit der Gleichung  ist.
ist.
Begründe damit, dass der Graph
(5 BE)
e)
Gib den maximalen Definitionsbereich des Terms  an. Bestimme
an. Bestimme  und deute das Ergebnis geometrisch.
und deute das Ergebnis geometrisch.
(4 BE)
f)
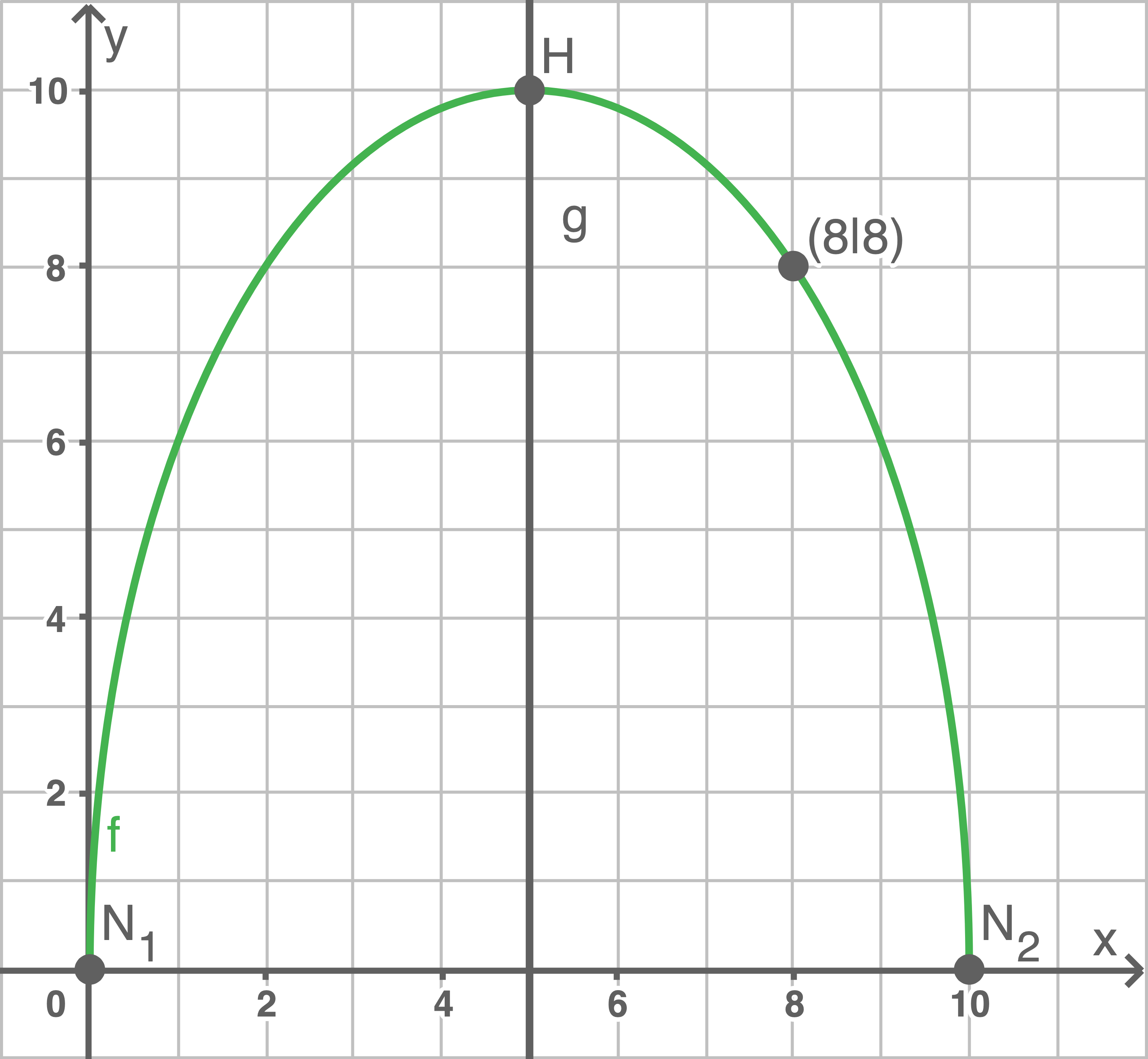
Gib  an und zeichne
an und zeichne  unter Berücksichtigung der bisherigen Ergebnisse in ein Koordinatensystem ein.
unter Berücksichtigung der bisherigen Ergebnisse in ein Koordinatensystem ein.
(4 BE)
g)
Betrachtet wird die Tangente  im Punkt
im Punkt  Berechne die Größe des Winkels, unter dem diese Tangente die
Berechne die Größe des Winkels, unter dem diese Tangente die  -Achse schneidet.
-Achse schneidet.
(2 BE)
h)
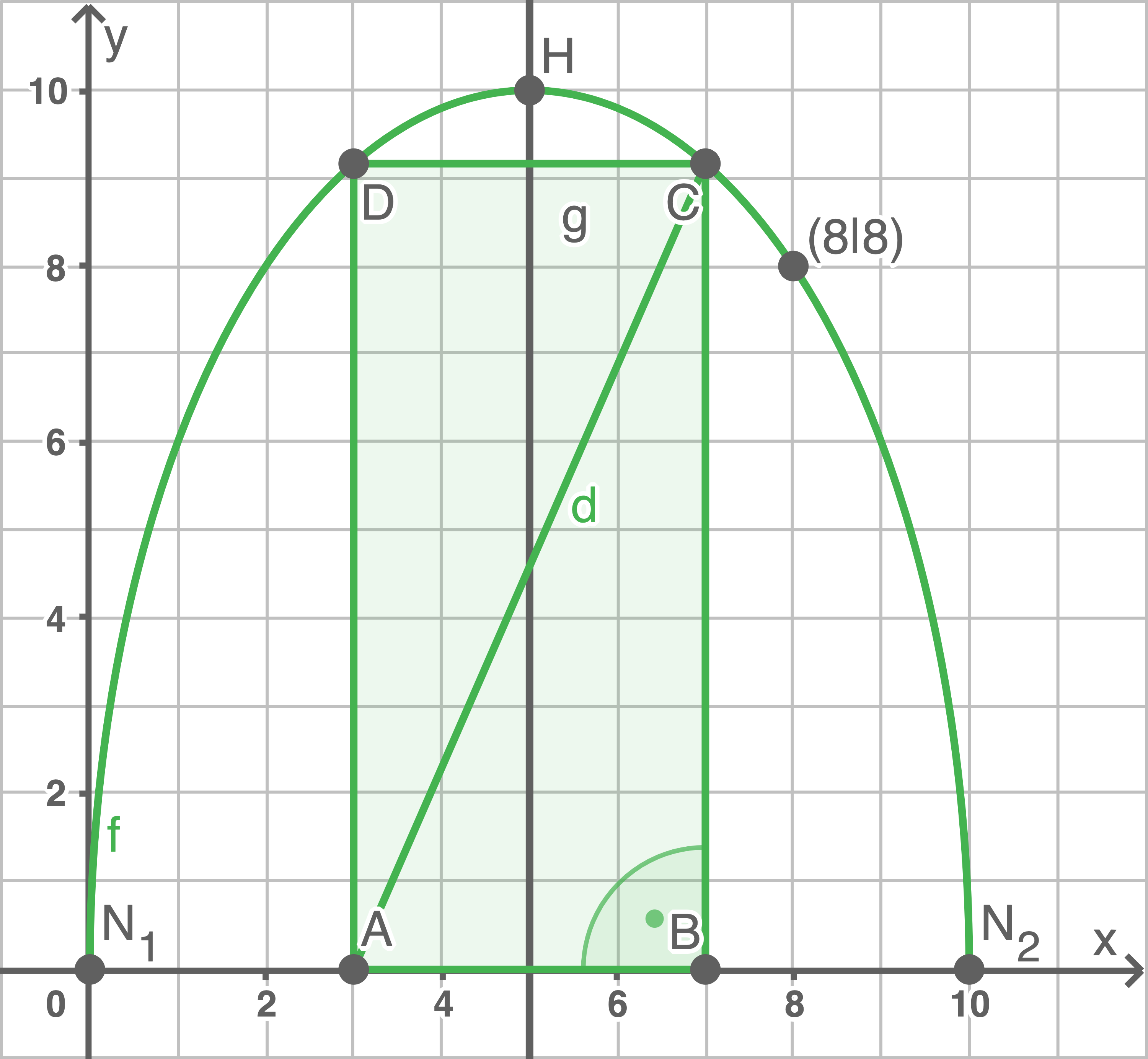
Von den Eckpunkten des Rechtecks  liegen der Punkt
liegen der Punkt  mit
mit ![\(s \in ] 0; 5[\)](https://mathjax.schullv.de/26bcd55ae62470214eafbb2ce76d5d1d731ae3e3d1f2e6e4374267d4d18fc5fc?color=5a5a5a) sowie der Punkt
sowie der Punkt  auf der
auf der  -Achse, die Punkte
-Achse, die Punkte  und
und  liegen auf
liegen auf  Das Rechteck besitzt somit die Gerade mit der Gleichung
Das Rechteck besitzt somit die Gerade mit der Gleichung  als Symmetrieachse. Zeige, dass die Diagonalen dieses Rechtecks jeweils die Länge
als Symmetrieachse. Zeige, dass die Diagonalen dieses Rechtecks jeweils die Länge  besitzen.
besitzen.
(5 BE)
Ein Wasserspeicher hat die Form eines geraden Zylinders und ist bis zu einem Füllstand von  über dem Speicherboden mit Wasser gefüllt. Bohrt man unterhalb des Füllstands ein Loch in die Wand des Wasserspeichers, so tritt unmittelbar nach Fertigstellung der Bohrung Wasser aus, das in einer bestimmten Entfernung zur Speicherwand auf den Boden trifft.
über dem Speicherboden mit Wasser gefüllt. Bohrt man unterhalb des Füllstands ein Loch in die Wand des Wasserspeichers, so tritt unmittelbar nach Fertigstellung der Bohrung Wasser aus, das in einer bestimmten Entfernung zur Speicherwand auf den Boden trifft.

i)
Der Graph  verläuft durch den Punkt
verläuft durch den Punkt  Gib die Bedeutung dieser Aussage im Sachzusammenhang an.
Gib die Bedeutung dieser Aussage im Sachzusammenhang an.
(1 BE)
j)
Berechne die Höhen, in denen das Loch gebohrt werden kann, damit die Spritzweite  beträgt. Gib zudem die Höhe an, in der das Loch gebohrt werden muss, damit die Spritzweite maximal ist.
beträgt. Gib zudem die Höhe an, in der das Loch gebohrt werden muss, damit die Spritzweite maximal ist.
(5 BE)
k)
Es wird nun ein bestimmtes Bohrloch im Wasserspeicher betrachtet. Durch das Abfließen verringert sich das Volumen des Wassers im Speicher in Abhängigkeit von der Zeit. Die Funktion  mit
mit  beschreibt modellhaft die zeitliche Entwicklung dieser Volumenänderung.
beschreibt modellhaft die zeitliche Entwicklung dieser Volumenänderung.
Dabei ist die seit der Fertigstellung des Bohrlochs vergangene Zeit in Sekunden und
die seit der Fertigstellung des Bohrlochs vergangene Zeit in Sekunden und  die momentane Änderungsrate des Wasservolumens im Speicher in Litern pro Sekunde.
die momentane Änderungsrate des Wasservolumens im Speicher in Litern pro Sekunde.
Berechne das Volumen des Wassers in Litern, das innerhalb der ersten Minute nach Fertigstellung des Bohrlochs aus dem Behälter abfließt.
Dabei ist
Berechne das Volumen des Wassers in Litern, das innerhalb der ersten Minute nach Fertigstellung des Bohrlochs aus dem Behälter abfließt.
(4 BE)
(40 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
b)
1. Schritt: Ableitung bilden



 2. Schritt: Notwendige Bedingung für Extremstellen anwenden
2. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/4ffabac0aff1a6af0402e6bdf6fa6c72a9979e30103529f37da0679f065e50cf?color=5a5a5a)


 Es gilt
Es gilt  und somit hat der einzige Punkt mit waagrechter Tangente den
und somit hat der einzige Punkt mit waagrechter Tangente den  -Wert 10, woraus sich ein Hochpunkt ergibt. Auf die hinreichende Bedingung für Extremstellen kann durch diese Überlegung verzichtet werden.
-Wert 10, woraus sich ein Hochpunkt ergibt. Auf die hinreichende Bedingung für Extremstellen kann durch diese Überlegung verzichtet werden.

c)
Es muss  gelten.
Es gilt:
gelten.
Es gilt:  In beiden Termen steht eine natürliche Zahl im Zähler und im Nenner ein Wurzelterm, dessen Wert aufgrund des Definitionsbereiches stets positiv ist.
Der Term der zweiten Ableitung muss wegen der Rechtskrümmung negativ sein, folglich müssen die Terme, die im Nenner vor der Wurzel stehen, untersucht werden:
In beiden Termen steht eine natürliche Zahl im Zähler und im Nenner ein Wurzelterm, dessen Wert aufgrund des Definitionsbereiches stets positiv ist.
Der Term der zweiten Ableitung muss wegen der Rechtskrümmung negativ sein, folglich müssen die Terme, die im Nenner vor der Wurzel stehen, untersucht werden:
 aus Term I ist in
aus Term I ist in ![\(]0; 10[\)](https://mathjax.schullv.de/e8ee95579c31dfe3365ccf451fefc7b4b1227c013aed6f9d7a1cc88051e9ffa4?color=5a5a5a) stets negativ.
stets negativ.
 aus Term II ist in
aus Term II ist in ![\(]0; 10[\)](https://mathjax.schullv.de/e8ee95579c31dfe3365ccf451fefc7b4b1227c013aed6f9d7a1cc88051e9ffa4?color=5a5a5a) stets positiv.
Somit stellt Term I die zweite Ableitung dar.
stets positiv.
Somit stellt Term I die zweite Ableitung dar.
d)
Die Gleichung ist also erfüllt.
Begründung
Die Punkte  und
und  haben denselben
haben denselben  -Wert und denselben Abstand auf der
-Wert und denselben Abstand auf der  -Achse zu 5.
Somit liegen die Punkte symmetrisch zur Geraden
-Achse zu 5.
Somit liegen die Punkte symmetrisch zur Geraden 
e)
Es gilt ![\( \mathbb{D}_f= [0;10] .\)](https://mathjax.schullv.de/f4b2d288a988ad7c85587e3a31dc0d2e22be21ee33a1b2e4165e5db49dea63c9?color=5a5a5a) In der ertsen Ableitung steht die Wurzel im Nenner, deshalb muss
In der ertsen Ableitung steht die Wurzel im Nenner, deshalb muss  gelten.
gelten.


 Die Funktion hat im Ursprung die höchste Steigung.
Die Funktion hat im Ursprung die höchste Steigung.
f)
g)
h)
i)
Wenn sich das Bohrloch in einer Höhe von  befindet, beträgt die Spritzweite
befindet, beträgt die Spritzweite 
j)
k)