Teil A
1
Gegeben ist die Funktion  mit maximalem Definitionsbereich
mit maximalem Definitionsbereich  .
.
a)
Gib  an und zeige, dass für den Term der Ableitungsfunktion
an und zeige, dass für den Term der Ableitungsfunktion  von
von  gilt:
gilt: 
(2 BE)
b)
Bestimme die Koordinaten des im II. Quadranten liegenden Hochpunkts des Graphen von  .
.
(3 BE)
2
Die Abbildung 1 zeigt den Graphen  der Ableitungsfunktion
der Ableitungsfunktion  einer in
einer in  definierten ganzrationalen Funktion
definierten ganzrationalen Funktion  Nur in den Punkten
Nur in den Punkten  und
und  hat der Graph
hat der Graph  waagrechte Tangenten.
waagrechte Tangenten.
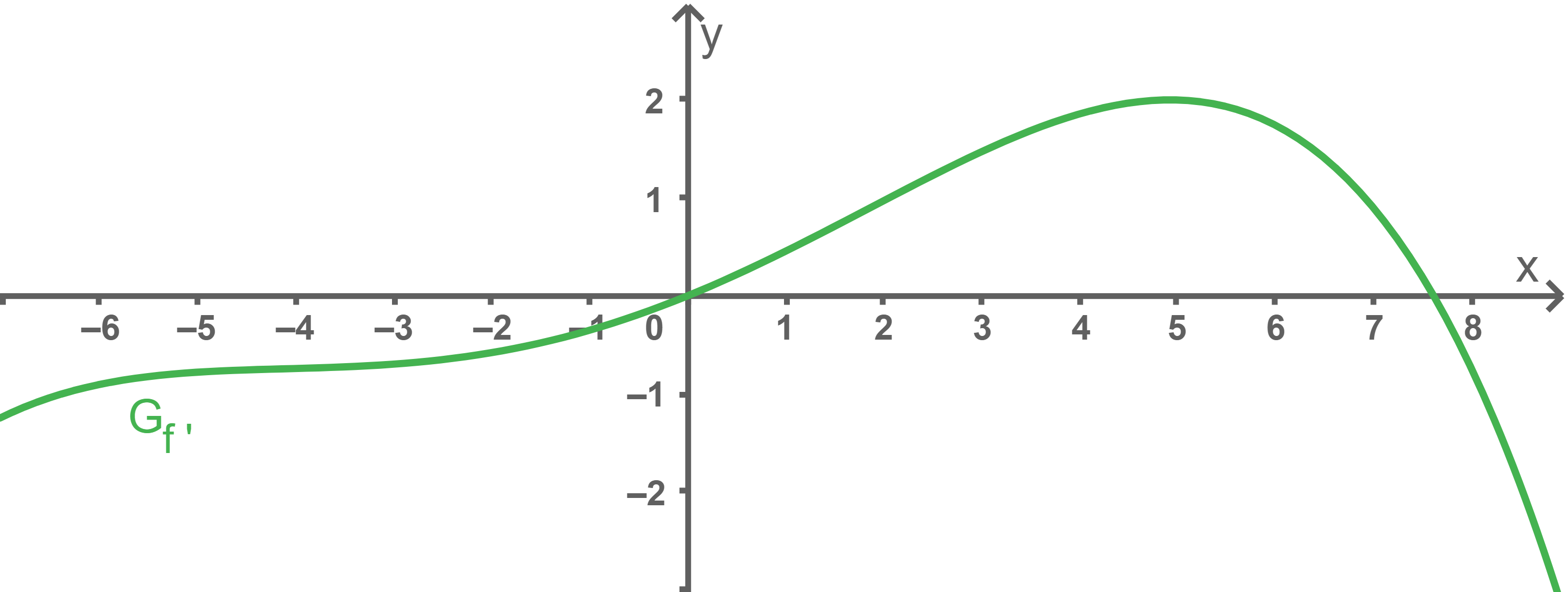

Abb. 1
a)
Begründe, dass  genau eine Wendestelle besitzt.
genau eine Wendestelle besitzt.
(2 BE)
b)
Es gibt Tangenten an den Graphen von  , die parallel zur Winkelhalbierenden des I. und III. Quadranten sind. Ermittle anhand des Graphen
, die parallel zur Winkelhalbierenden des I. und III. Quadranten sind. Ermittle anhand des Graphen  der Ableitungsfunktion
der Ableitungsfunktion  in der Abbildung 1 Näherungswerte für die
in der Abbildung 1 Näherungswerte für die  -Koordinaten derjenigen Punkte, in denen der Graph von
-Koordinaten derjenigen Punkte, in denen der Graph von  jeweils eine solche Tangente hat.
jeweils eine solche Tangente hat.
(2 BE)
3
Gegeben sind die in  definierten Funktionen
definierten Funktionen  und
und  mit
mit  . Der Graph von
. Der Graph von  wird mit
wird mit  und der Graph von
und der Graph von  mit
mit  bezeichnet.
bezeichnet.
a)
Skizziere  in einem Koordinatensystem. Berechne die Koordinaten des gemeinsamen Punkts der Graphen
in einem Koordinatensystem. Berechne die Koordinaten des gemeinsamen Punkts der Graphen  und
und  .
.
(3 BE)
b)
Es gibt Werte von  , für die die Graphen
, für die die Graphen  und
und  jeweils keinen gemeinsamen Punkt haben. Gib diese Werte von
jeweils keinen gemeinsamen Punkt haben. Gib diese Werte von  an.
an.
(2 BE)
4
Gegeben ist die Funktion  mit
mit  und
und  .
.
Die Funktion ist umkehrbar. Die Abbildung 2 zeigt den Graphen
ist umkehrbar. Die Abbildung 2 zeigt den Graphen  von
von  sowie einen Teil des Graphen
sowie einen Teil des Graphen  der Umkehrfunktion
der Umkehrfunktion  von
von 
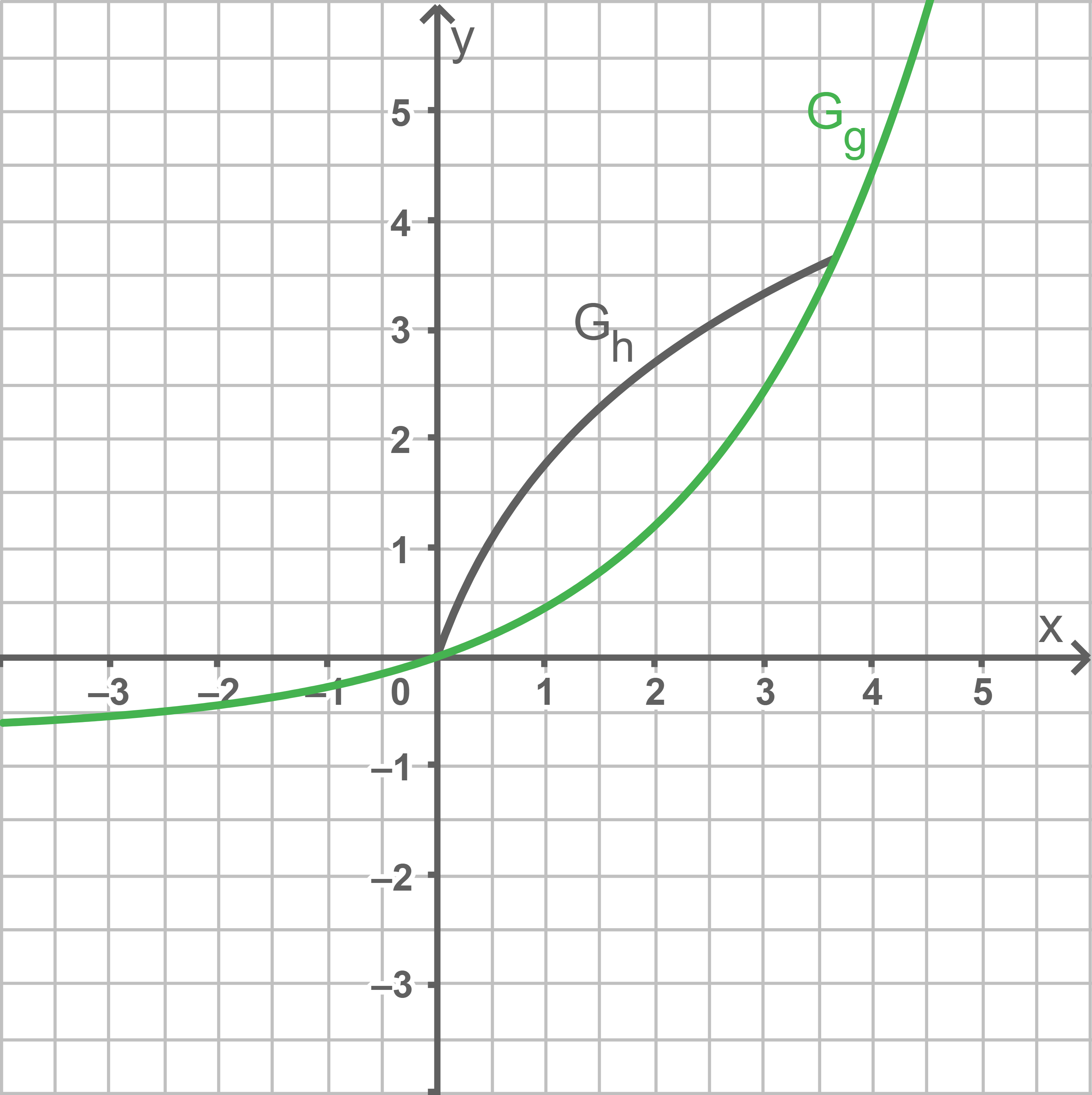
Die Funktion

Abb. 2
a)
Zeichne in die Abbildung 2 den darin fehlenden Teil von  ein.
ein.
(2 BE)
b)
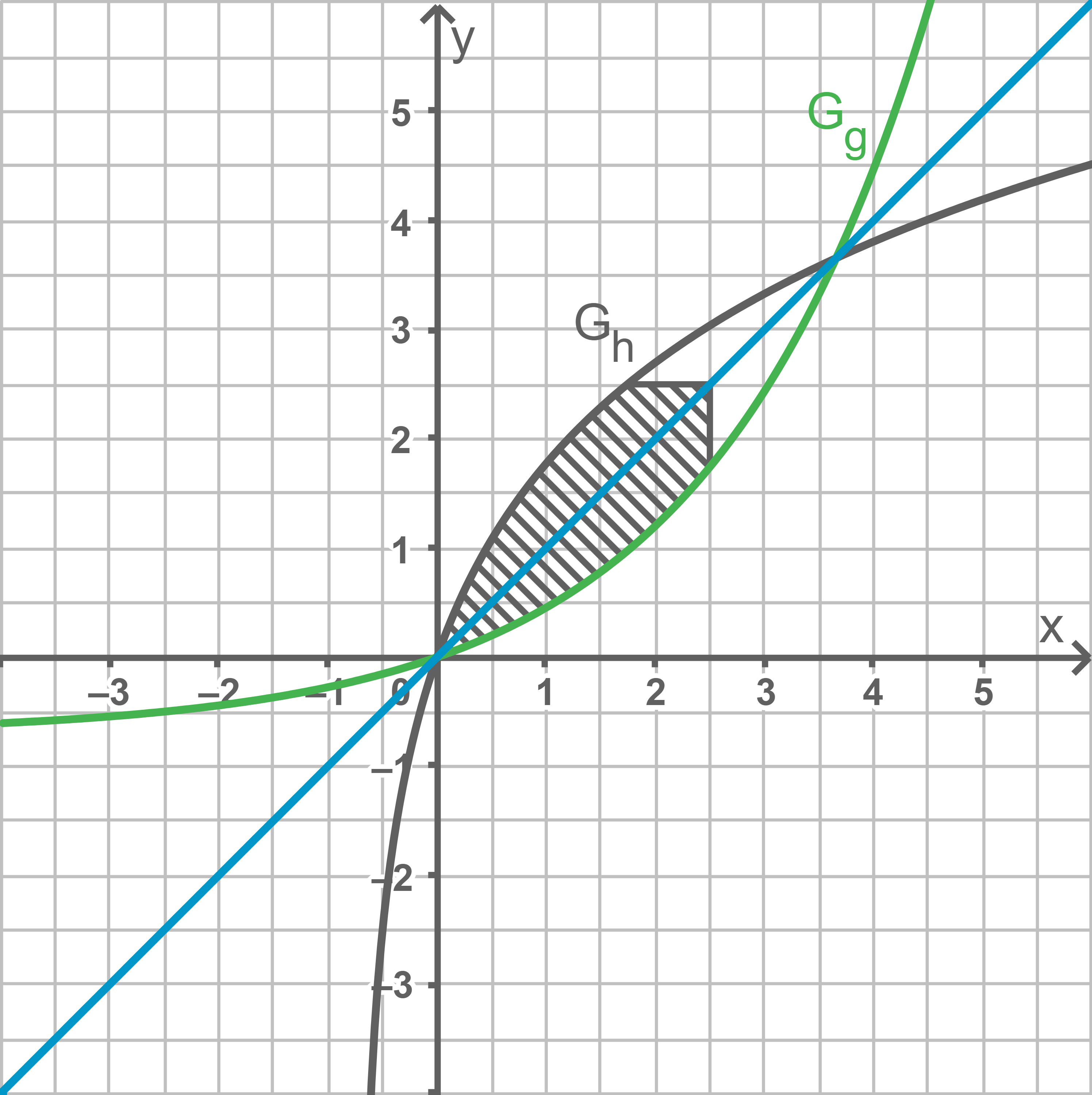
Betrachtet wird das von den Graphen  und
und  eingeschlossene Flächenstück. Schraffiere den Teil dieses Flächenstücks, dessen Inhalt mit dem Term
eingeschlossene Flächenstück. Schraffiere den Teil dieses Flächenstücks, dessen Inhalt mit dem Term  berechnet werden kann.
berechnet werden kann.
(2 BE)
c)
Gib den Term einer Stammfunktion der in  definierten Funktion
definierten Funktion  an.
an.
(2 BE)
(20 BE)
1
a)
b)
Anwendung der notwendigen Bedingung für Extremstellen liefert:
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/ab20c4b87845098eb2f1f23546d0b96db4f3a97736d109b6f12769864bcf4eb2?color=5a5a5a) Da stets
Da stets  gilt, kann nur der Funktionswert an der Stelle
gilt, kann nur der Funktionswert an der Stelle  im II. Quadranten liegen. Da laut Aufgabenstellung ein Hochpunkt im zweiten Quadranten existiert, muss die hinreichende Bedingung hier nicht überprüft werden.
im II. Quadranten liegen. Da laut Aufgabenstellung ein Hochpunkt im zweiten Quadranten existiert, muss die hinreichende Bedingung hier nicht überprüft werden.
Mit

 ergeben sich die Koordinaten des gesuchten Hochpunkts als
ergeben sich die Koordinaten des gesuchten Hochpunkts als 
Mit
2
a)
Dass  in einem Punkt eine waagrechte Tangente besitzt bedeutet, dass
in einem Punkt eine waagrechte Tangente besitzt bedeutet, dass  in diesem Punkt den Wert Null annimmt und somit die notwendige Bedingung für eine Wendestelle erfüllt ist.
Die Abbildung liefert, dass
in diesem Punkt den Wert Null annimmt und somit die notwendige Bedingung für eine Wendestelle erfüllt ist.
Die Abbildung liefert, dass  im Punkt
im Punkt  einen Sattelpunkt besitzt. Die Steigung von
einen Sattelpunkt besitzt. Die Steigung von  ist hier somit sowohl links als auch rechts von
ist hier somit sowohl links als auch rechts von  positiv, das heißt
positiv, das heißt  besitzt in der Stelle
besitzt in der Stelle  keinen Vorzeichenwechsel. Somit liegt dort keine Wendestelle von
keinen Vorzeichenwechsel. Somit liegt dort keine Wendestelle von  vor.
vor.
An der Stelle besitzt
besitzt  eine Wendestelle, da hier der Hochpunkt von
eine Wendestelle, da hier der Hochpunkt von  liegt und die Steigung von
liegt und die Steigung von  damit links davon positiv ist und rechts von
damit links davon positiv ist und rechts von  negativ.
Da
negativ.
Da  nur an diesen beiden Stellen eine waagrechte Tangente hat, besitzt die Funktion
nur an diesen beiden Stellen eine waagrechte Tangente hat, besitzt die Funktion  somit genau eine Wendestelle.
somit genau eine Wendestelle.
An der Stelle
b)
Die Winkelhalbierende des I. und III. Quadranten hat die Gleichung  und somit die Steigung
und somit die Steigung 
Vergleichen mit den Funktionswerten von anhand des Graphen
anhand des Graphen  liefert somit, dass der Graph von
liefert somit, dass der Graph von  bei ca.
bei ca.  und ca.
und ca.  Tangenten besitzt, die parallel zur Winkelhalbierenden des ersten Quadranten sind.
Tangenten besitzt, die parallel zur Winkelhalbierenden des ersten Quadranten sind.
Vergleichen mit den Funktionswerten von
3
a)
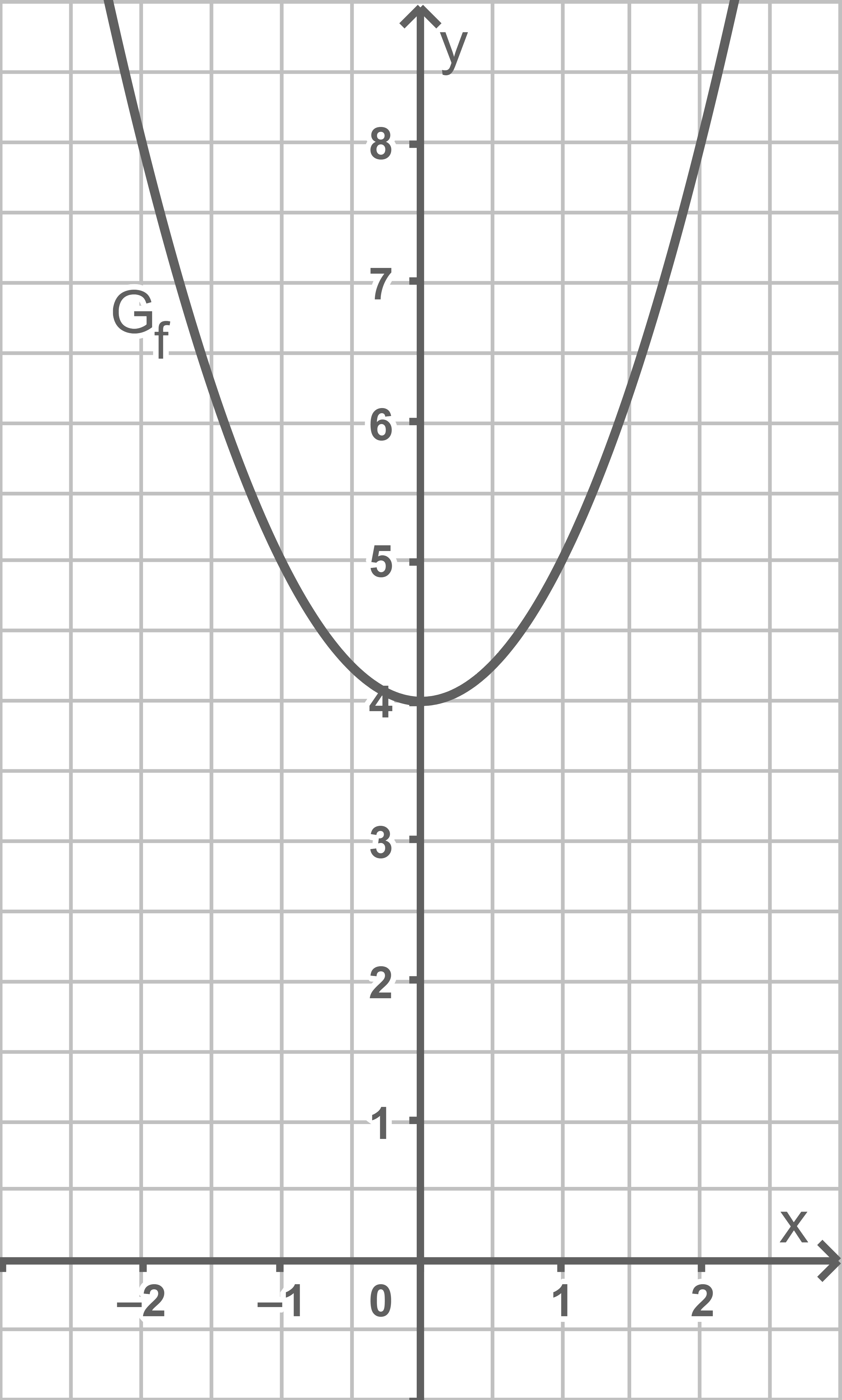
b)
4
a)
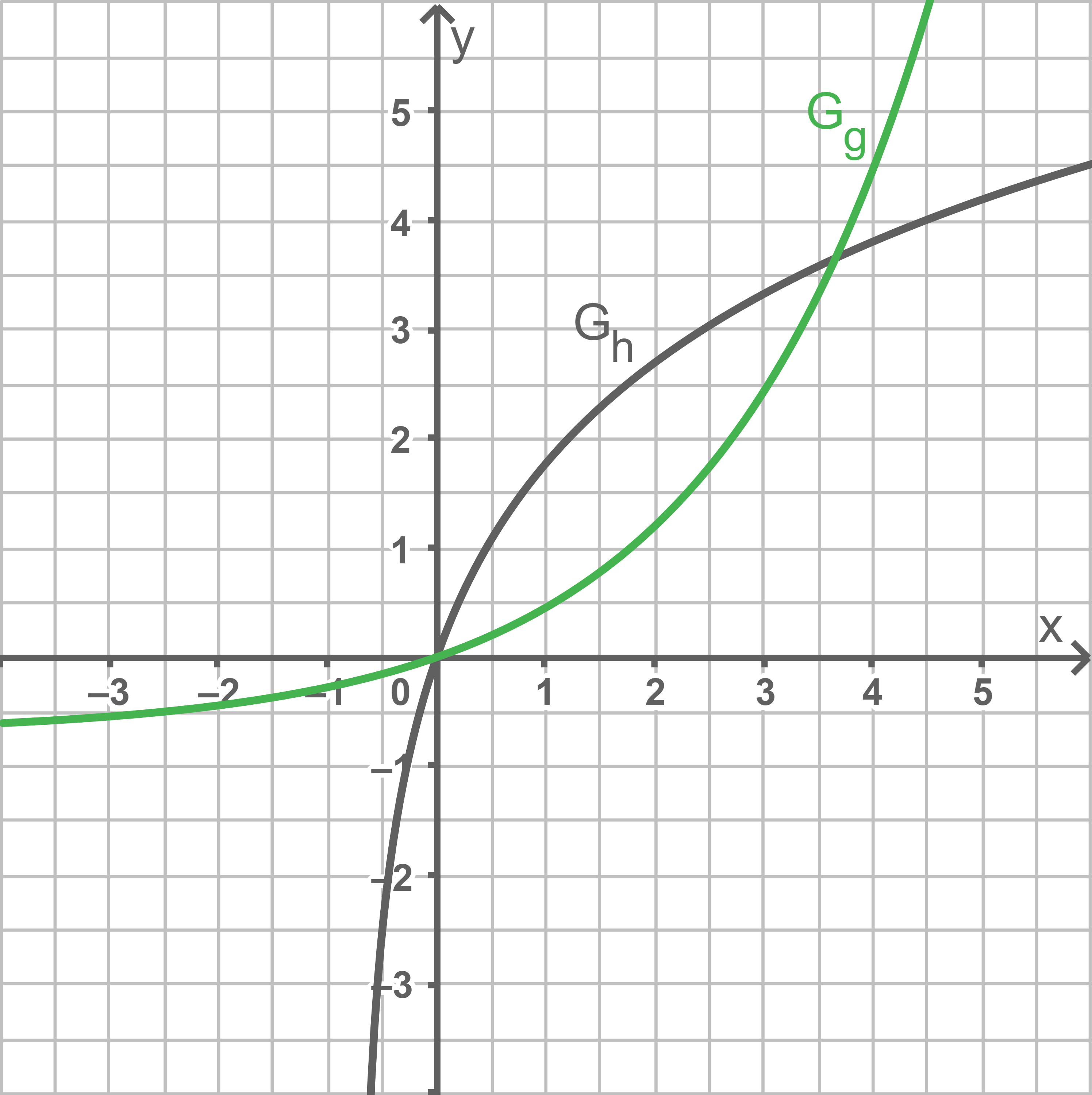
b)
c)
Mit Hilfe der Stammfunktionen von  und
und  ergibt sich für den Term einer Stammfunktion von
ergibt sich für den Term einer Stammfunktion von  z.B.
z.B. 