Teil A
Gegeben sind die im Folgenden beschriebenen Zufallsgrößen  und
und  :
:
- Ein Würfel, dessen Seiten mit den Zahlen von
bis
durchnummeriert sind, wird zweimal geworfen.
gibt die dabei erzielte Augensumme an.
- Aus einem Behälter mit
schwarzen und
weißen Kugeln wird zwölfmal nacheinander jeweils eine Kugel zufällig entnommen und wieder zurücklegt.
gibt die Anzahl der entnommenen schwarzen Kugeln an.
a)
Begründe, dass die Wahrscheinlichkeit  mit der Wahrscheinlichkeit
mit der Wahrscheinlichkeit  übereinstimmt.
übereinstimmt.
(2 BE)
b)
Die Wahrscheinlichkeitsverteilungen von  und
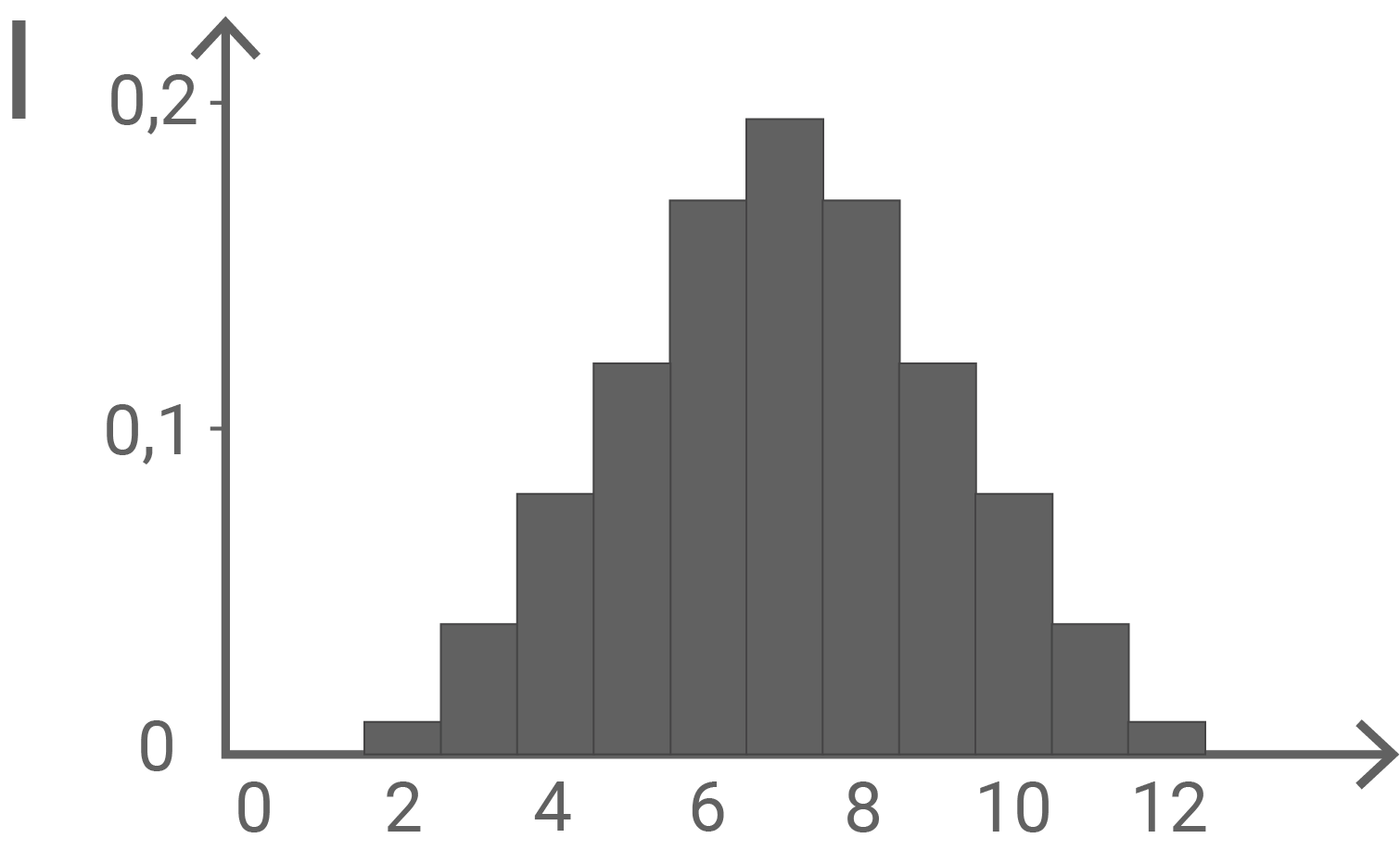
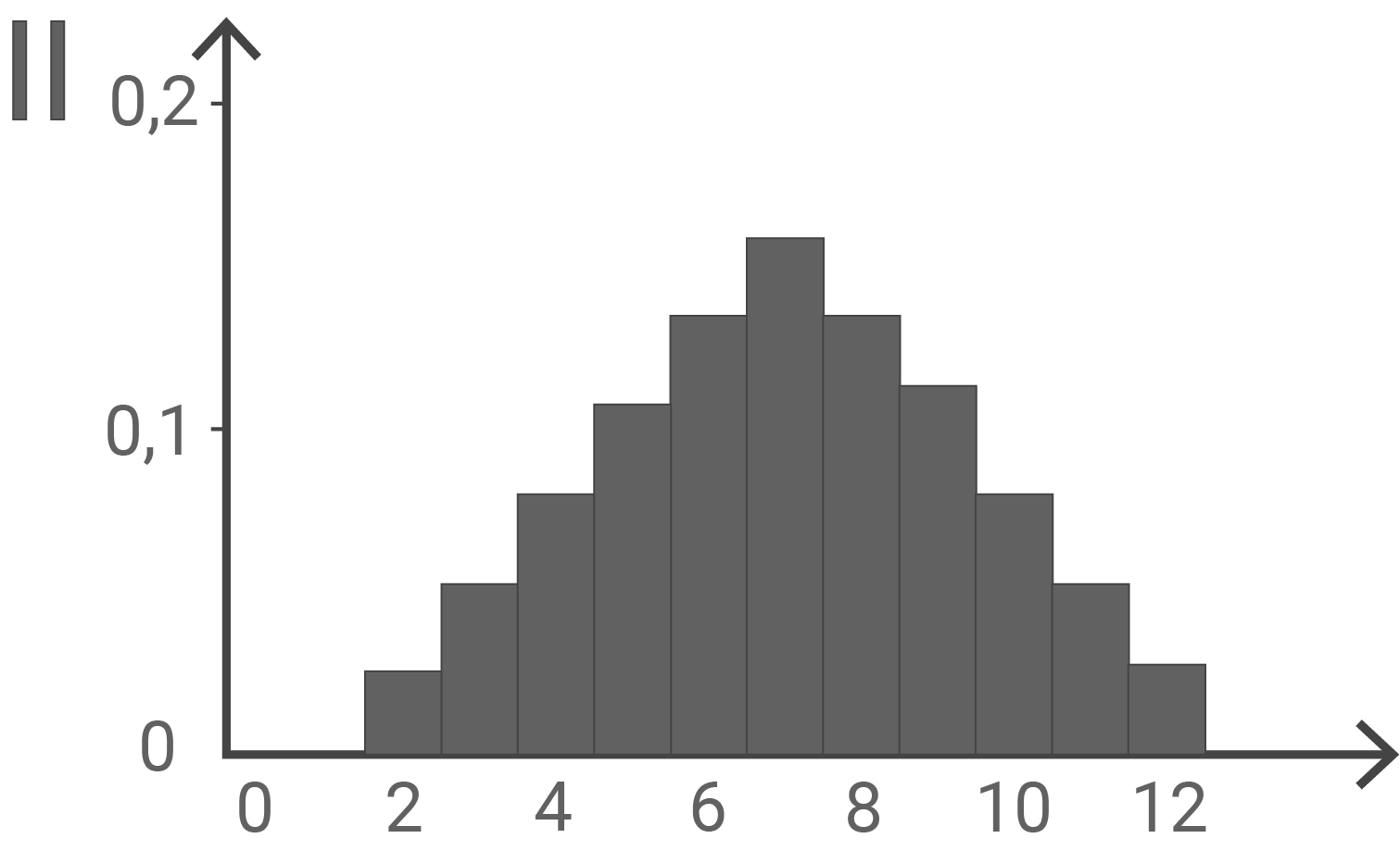
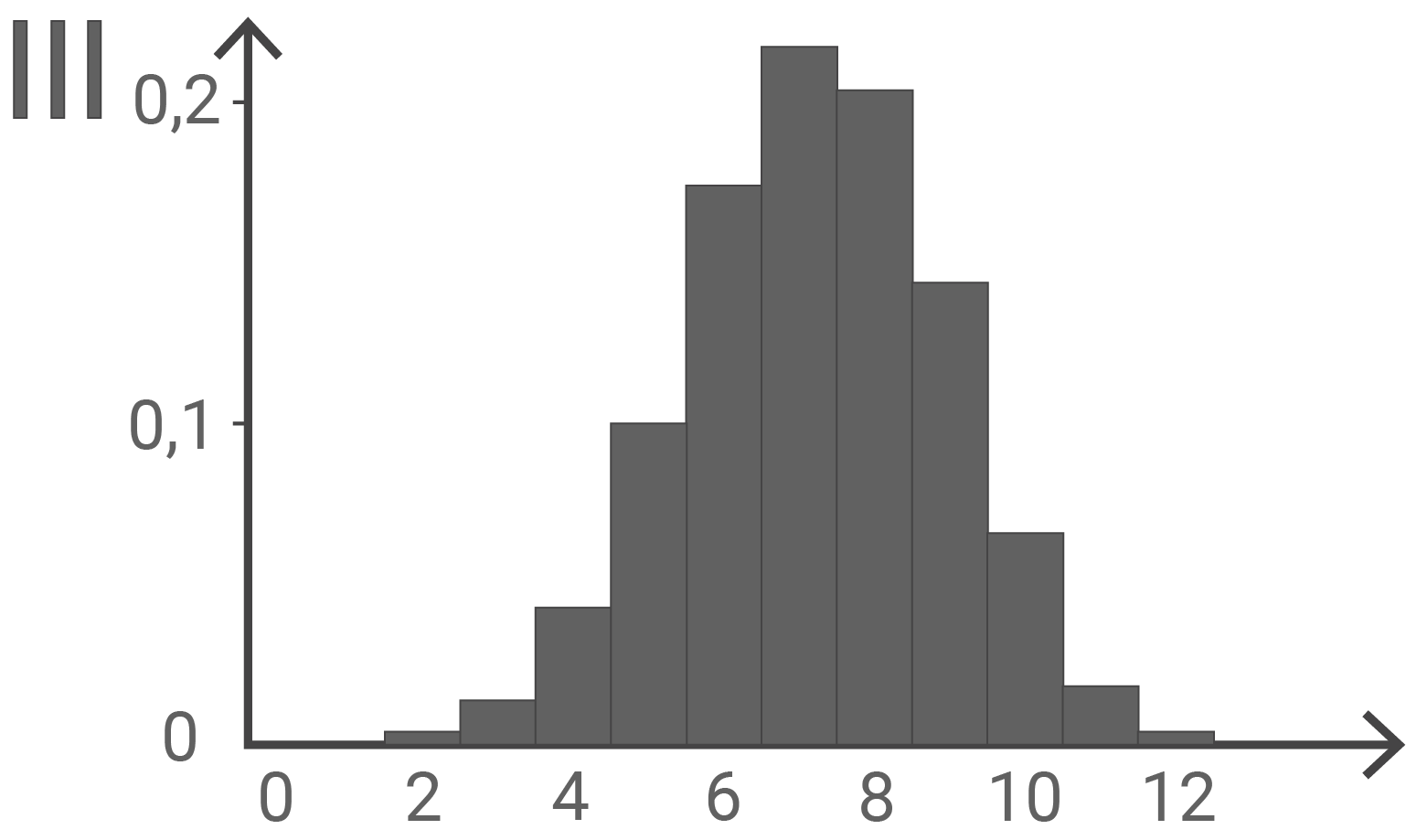
und  werden jeweils durch eines der folgenden Diagramme I, II und III dargestellt. Ordne
werden jeweils durch eines der folgenden Diagramme I, II und III dargestellt. Ordne  und
und  jeweils dem passenden Diagramm zu und begründe deine Zuordnung.
jeweils dem passenden Diagramm zu und begründe deine Zuordnung.
(3 BE)



(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Beiden Augensummen liegt die gleiche Anzahl an möglichen Ergebnissen mit jeweils der Wahrscheinlichkeit  zu Grunde:
zu Grunde:



 Somit beträgt die Wahrscheinlichkeit für
Somit beträgt die Wahrscheinlichkeit für  genau wie die für
genau wie die für  genau
genau 
b)
Die symmetrische Wahrscheinlichkeitsverteilung von  wird durch Diagramm II dargestellt: Die Wahrscheinlichkeit
wird durch Diagramm II dargestellt: Die Wahrscheinlichkeit  ist doppelt so groß wie
ist doppelt so groß wie  Außerdem sind alle Wahrscheinlichkeiten von
Außerdem sind alle Wahrscheinlichkeiten von  ganzzahlige Vielfache von
ganzzahlige Vielfache von  . Das trifft nur auf Diagramm II zu.
. Das trifft nur auf Diagramm II zu.
 ist binomialverteilt mit
ist binomialverteilt mit  die Wahrscheinlichkeitsverteilung von
die Wahrscheinlichkeitsverteilung von  ist somit nicht symmetrisch und wird damit durch Abbildung III dargestellt.
ist somit nicht symmetrisch und wird damit durch Abbildung III dargestellt.